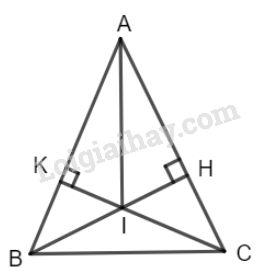
Bài 65 trang 137 SGK Toán 7 tập 1Cho tam giác ABC cân tại A Đề bài Cho tam giác ABCABC cân tại AA (ˆAˆA< 90o90o). Vẽ BH⊥ACBH⊥AC (HH thuộc ACAC), CK⊥ABCK⊥AB (KK thuộc ABAB) a) Chứng minh rằng AH=AK.AH=AK. b) Gọi II là giao điểm của BHBH và CKCK. Chứng minh rằng tia AIAI là tia phân giác của góc A.A. Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Nếu canh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. - Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Lời giải chi tiết
a) ΔABHΔABH vuông tại HH; ΔACKΔACK vuông tại KK. Xét hai tam giác vuông ABHABH và ACKACK có: +) AB=ACAB=AC (vì tam giác ABCABC cân tại AA) +) ˆAˆA chung ⇒ΔABH=ΔACK⇒ΔABH=ΔACK (cạnh huyền - góc nhọn). ⇒AH=AK⇒AH=AK (hai cạnh tương ứng). b) ΔAIKΔAIK vuông tại KK; ΔAIHΔAIH vuông tại HH. Xét hai tam giác vuông AIKAIK và AIHAIH có: +) AK=AHAK=AH (chứng minh trên) +) AIAI cạnh chung ⇒ΔAIK=ΔAIH⇒ΔAIK=ΔAIH (cạnh huyền- cạnh góc vuông) ⇒^IAK=^IAH⇒ˆIAK=ˆIAH (hai góc tương ứng) Vậy AI là tia phân giác của góc A. HocTot.Nam.Name.Vn
|