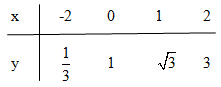Bài 62 sách giải tích 12 nâng cao trang 118Vẽ đồ thị của hàm số . Dựa vào đồ thị, hãy giải thích các bất phương trình sau:
Lựa chọn câu để xem lời giải nhanh hơn
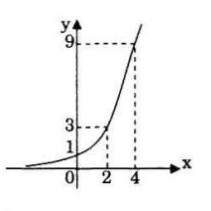
Vẽ đồ thị của hàm số \(y = {\left( {\sqrt 3 } \right)^x}\). Dựa vào đồ thị, hãy giải các bất phương trình sau: a) \({\left( {\sqrt 3 } \right)^x} \le 1\); b) \({\left( {\sqrt 3 } \right)^x} > 3\). LG a \({\left( {\sqrt 3 } \right)^x} \le 1\); Lời giải chi tiết: * Vẽ đồ thị của hàm số \(y = {\left( {\sqrt 3 } \right)^x}\) TXĐ: \(D =\mathbb R\) Hàm số đồng biến trên R.
* Giải bất phương trình \({\left( {\sqrt 3 } \right)^x} \le 1\) \({\left( {\sqrt 3 } \right)^x} \le 1 \Leftrightarrow x \le 0\) (ứng với những điểm trên đồ thị có tung độ nhỏ hơn hoặc bằng 1) Quảng cáo  LG b \({\left( {\sqrt 3 } \right)^x} > 3\) Lời giải chi tiết: TXĐ: \(D =\mathbb R\) Hàm số đồng biến trên R.
\({\left( {\sqrt 3 } \right)^x} > 3 \Leftrightarrow x > 2\) (ứng với những điểm trên đồ thị có tung độ lớn hơn 3). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|
