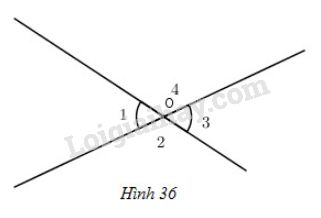
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học

Bài 52 trang 101 SGK Toán 7 tập 1

Xem hình 36, hãy điền vào chỗ trống(...) để chứng minh định lí: " Hai góc đối đỉnh thì bằng nhau".

Đề bài

Xem hình $36$ , hãy điền vào chỗ trống (...) để chứng minh định lí: " Hai góc đối đỉnh thì bằng nhau".

GT: ...

KL: ...

Các khẳng định		Căn cứ của khẳng định
1	$\widehat{O_{1}}$ + $\widehat{O_{2}}=180^0$	Vì …
2	$\widehat{O_{3}}$ + $\widehat{O_{2}}$ = ...	Vì …
3	$\widehat{O_{1}}$ + $\widehat{O_{2}}$ = $\widehat{O_{3}}$ + $\widehat{O_{2}}$	Căn cứ vào …
4	$\widehat{O_{1}}$ = $\widehat{O_{3}}$	Căn cứ vào …

Tương tự chứng minh $\widehat{O_{2}} = \widehat{O_{4}}$

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Hai góc đối đỉnh thì bằng nhau.

- Hai góc kề bù có tổng bằng $180^0.$

Lời giải chi tiết

Giả thiết: $\widehat{O_{1}}$ đối đỉnh với $\widehat{O_{3}}$ .

Kết luận: $\widehat{O_{1}} = \widehat{O_{3}}$

Các khẳng định		Căn cứ của khẳng định
1	$\widehat{O_{1}}$ + $\widehat{O_{2}}=180^0$	Vì $\widehat{O_{1}}$ và $\widehat{O_{2}}$ kề bù
2	$\widehat{O_{3}}$ + $\widehat{O_{2}}=180^0$	Vì $\widehat{O_{2}}$ và $\widehat{O_{3}}$ kề bù
3	$\widehat{O_{1}}$ + $\widehat{O_{2}}$ = $\widehat{O_{3}}$ + $\widehat{O_{2}}$	Căn cứ vào khẳng định 1 và 2
4	$\widehat{O_{1}}$ = $\widehat{O_{3}}$	Căn cứ vào khẳng định 3

Tương tự:

Giả thiết: $\widehat{O_{2}}$ đối đỉnh với $\widehat{O_{4}}$ .

Kết luận: $\widehat{O_{2}} = \widehat{O_{4}}$

Các khẳng định		Căn cứ của khẳng định
1	$\widehat{O_{1}}$ + $\widehat{O_{2}}=180^0$	Vì $\widehat{O_{1}}$ và $\widehat{O_{2}}$ kề bù
2	$\widehat{O_{1}}$ + $\widehat{O_{4}}=180^0$	Vì $\widehat{O_{1}}$ và $\widehat{O_{4}}$ kề bù
3	$\widehat{O_{1}}$ + $\widehat{O_{2}}$ = $\widehat{O_{1}}$ + $\widehat{O_{4}}$	Căn cứ vào khẳng định 1 và 2
4	$\widehat{O_{2}}$ = $\widehat{O_{4}}$	Căn cứ vào khẳng định 3

HocTot.Nam.Name.Vn

Chia sẻ

Bình luận

Bình chọn:

4.5 trên 283 phiếu

Bài 53 trang 102 SGK Toán 7 tập 1
Cho định lí: " Nếu hai đường thẳng xx', yy' cắt nhau tại O góc xOy vuông thì các góc yOx', x'Oy', y'Ox đều là góc vuông".
Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 1 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 1 - Hình học 7
Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 1 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 1 - Hình học 7
Bài 51 trang 101 SGK Toán 7 tập 1
Hãy viết định lí nói về một đường thẳng vuông góc với một trong hai đường thẳng song song.
Bài 50 trang 101 SGK Toán 7 tập 1
Hãy viết kết luận của định lí sau bằng cách điền vào chỗ trống (...)

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link

Bài 52 trang 101 SGK Toán 7 tập 1

Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Góp ý

Báo lỗi góp ý

Báo lỗi