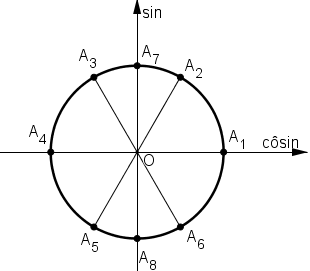
Giải bài 5 trang 29 SGK Đại số và Giải tích 11

LG a

\(\begin{array}{l}\tan \left( {x - {{15}^0}} \right) = \frac{{\sqrt 3 }}{3}\\\end{array}\)

Phương pháp giải:

Coi biểu thức sau hàm tan như một ẩn phụ khác, giải tương tự như pt LG cơ bản

\(\begin{array}{l}
\,\,\tan x = \tan a \Leftrightarrow x =a + k180^0 \\ \left( {k \in Z} \right)\\\end{array}\)

Lời giải chi tiết:

Điều kiện \(x - 15^0\neq 90^0+k180^0 \) \(\Leftrightarrow x\neq 105^0+k.180^0.\)

\(tan (x - 15^0) = \frac{\sqrt{3}}{3}\)

\( \Leftrightarrow tan(x-15^0)=tan30^0\)

\(\Leftrightarrow x - 15^0 = 30^0 + k180^0 , (k \in \mathbb{Z}).\)

\(\Leftrightarrow x = 45^0 + k180^0 , (k \in \mathbb{Z}).\) (tm)

Vậy nghiệm của phương trình là: \(x = 45^0 + k180^0 , (k \in \mathbb{Z}).\)

LG b

\(\begin{array}{l}\,\,\cot \left( {3x - 1} \right) = - \sqrt 3 \\\end{array}\)

Phương pháp giải:

Coi biểu thức sau hàm cot như một ẩn phụ lớn, giải tương tự như pt LG cơ bản

\(\begin{array}{l}\,\,\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \,\,\,\left( {k \in Z} \right)\\\end{array}\)

Lời giải chi tiết:

Điều kiện \(3x-1\neq k\pi (k\in \mathbb{Z})\) hay \(x\neq \frac{1+k \pi}{3}(k\in \mathbb{Z})\)

\(\begin{array}{l}
\,\,\,\,\,\,\cot \left( {3x - 1} \right) = - \sqrt 3 \\ \Leftrightarrow \cot \left( {3x - 1} \right) = \cot \left( { - \frac{\pi }{6}} \right)\\
\Leftrightarrow 3x - 1 = - \frac{\pi }{6} + k\pi \\
\Leftrightarrow 3x = 1 - \frac{\pi }{6} + k\pi \\
\Leftrightarrow x = \frac{1}{3} - \frac{\pi }{{18}} + \frac{{k\pi }}{3}\,\,\left( {k \in Z} \right)\,\,\left( {tm} \right)
\end{array}\)

Vậy nghiệm phương trình là \(x=\frac{1}{3}-\frac{\pi }{18}+\frac{k\pi }{3},(k\in \mathbb{Z})\)

LG c

\(\begin{array}{l}\,\,\cos 2x\tan x = 0\\\end{array}\)

Phương pháp giải:

\(\begin{array}{l}\,\,AB = 0 \Leftrightarrow \left[ \begin{array}{l}
A = 0\\
B = 0
\end{array} \right.
\end{array}\)

Lưu ý điều kiện xác định của các hàm tan và cot, hàm phân thức.

Lời giải chi tiết:

Điều kiện \(cosx\neq 0\Leftrightarrow x\neq \frac{\pi }{2}+k\pi (k\in \mathbb{Z})\)

\(\begin{array}{l}
\,\,\,\,\,\,\cos 2x\tan x = 0\\
\Leftrightarrow \left[ \begin{array}{l}
\cos 2x = 0\\
\tan x = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
2x = \frac{\pi }{2} + k\pi \\
x = k\pi 
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{4} + \frac{{k\pi }}{2}\\
x = k\pi 
\end{array} \right.\,\,\left( {k \in Z} \right)\,\,\,\left( {tm} \right)
\end{array}\)

Vậy nghiệm phương trình là: \(x=\frac{\pi }{4}+\frac{k\pi }{2}(k\in \mathbb{Z})\) hoặc \(x=k\pi (k\in \mathbb{Z})\)

LG d

\(\begin{array}{l}\,\,\sin 3x\cot x = 0
\end{array}\)

Phương pháp giải:

\(\begin{array}{l}\,\,AB = 0 \Leftrightarrow \left[ \begin{array}{l}
A = 0\\
B = 0
\end{array} \right.
\end{array}\)

Lưu ý điều kiện xác định của các hàm tan và cot, hàm phân thức.

Lời giải chi tiết:

ĐK: \(sinx\neq 0\Leftrightarrow x\neq k\pi (k\in \mathbb{Z})\)

\(\begin{array}{l}
\,\,\,\,\,\sin 3x\cot x = 0\\
\Leftrightarrow \left[ \begin{array}{l}
\sin 3x = 0\\
\cot x = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
3x = k\pi \\
x = \frac{\pi }{2} + n\pi 
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{{k\pi }}{3}\\
x = \frac{\pi }{2} + n\pi 
\end{array} \right.\,\,\,\left( {k,n \in Z} \right)
\end{array}\)

Kết hợp với điều kiện ta thấy khi \(k = 3m,m \in \mathbb{Z}\) thì \(x = \frac{{k\pi }}{3} = \frac{{3m\pi }}{3} = m\pi \,\,\left( {m \in Z} \right)\) \( \Rightarrow \sin x = 0\) không thỏa điều kiện.

Vậy phương trình có nghiệm là: \(x=\frac{k \pi}{3}\) \(\,\left( {k \ne 3m\,\,\left( {m \in Z} \right)} \right)\) và \(x=\frac{\pi }{2}+n\pi \,\,(n \in Z)\).

Chú ý:

Biểu diễn các họ nghiệm trên đường tròn lượng giác để loại nghiệm:

Các nghiệm \(\left[ \begin{array}{l}x = \dfrac{{k\pi }}{3}\\x = \dfrac{\pi }{2} + k\pi \end{array} \right.,k \in \mathbb{Z}\) được biểu diễn bởi các điểm từ A₁ đến A₈ trên đường tròn lượng giác như hình dưới.

Với điều kiện x ≠ k.π nên các điểm A₁ và A₄ bị loại.

Vậy họ nghiệm chỉ còn lại các điểm A₂; A₃; A₅; A₆; A₇; A₈ và ta viết được dưới kết quả \(\left[ \begin{array}{l}x =  \pm \dfrac{\pi }{3} + k\pi \\x = \dfrac{\pi }{2} + k\pi \end{array} \right.,k \in \mathbb{Z}\).

HocTot.Nam.Name.Vn