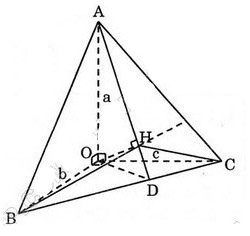
Bài 5 trang 26 SGK Hình học 12

Đề bài

Cho hình chóp tam giác $O.ABC$ có ba cạnh $OA, OB, OC$ đôi một vuông góc với nhau và $OA = a, OB = b, OC = c$. Hãy tính đường cao $OH$ của hình chóp.

Lời giải chi tiết

Kẻ $\displaystyle AD\,\bot \, BC, OH  \, \bot  \, AD$ ta chứng minh $\displaystyle OH$ chính là đường cao của hình chóp.

$\displaystyle \begin{array}{l} \left\{ \begin{array}{l} BC \,  \bot  \, OA\\ BC  \, \bot  \, AH \end{array} \right. \Rightarrow BC \,  \bot  \, \left( {OAH} \right) \\\Rightarrow BC  \, \bot  \, OH\,\,\,\,\left( 1 \right)\\ \left\{ \begin{array}{l} AC \,  \bot  \, BH\\ AC  \, \bot  \, OB \end{array} \right. \Rightarrow AC  \, \bot  \, \left( {OBH} \right) \\\Rightarrow AC  \, \bot  \, OH\,\,\,\,\left( 2 \right)\\ \left( 1 \right);\left( 2 \right) \Rightarrow OH  \, \bot  \, \left( {ABC} \right) \end{array}$

Vậy $\displaystyle OH$ chính là đường cao của hình chóp.

$\displaystyle BC  \, \bot  \, \left( {OAH} \right) \Rightarrow BC  \, \bot  \, \left( {OAD} \right)$ $\Rightarrow BC \bot OD$.

Tam giác $OBC$ vuông tại $O$ nên $BC = \sqrt {O{B^2} + O{C^2}}  = \sqrt {{b^2} + {c^2}}$

Áp dụng hệ thức lượng trong tam giác vuông $OBC$ ta có:

$\displaystyle OD.BC = OB.OC$ nên $\displaystyle OD  = \frac{{OB.OC}}{{BC}}={{bc} \over {\sqrt {{b^2} + {c^2}} }}$.

Áp dụng định lí Pitago trong tam giác vuông $OAD$ ta có:

$\displaystyle AD  = \sqrt {A{O^2} + O{D^2}}$ $= \sqrt {{a^2} + \dfrac {{b^2}{c^2}}  {{b^2} + {c^2}}}$ 

$\displaystyle = \sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}}$ .

Áp dụng hệ thức lượng trong tam giác vuông $OAD$ ta có: $\displaystyle OH.AD = OA.OD$ nên

$\displaystyle OH  = \dfrac{{OA.OD}}{{AD}}$ $=\displaystyle {{abc} \over {\sqrt {{b^2} + {c^2}} }}:\sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}}$ $\displaystyle = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}$.

Cách khác:

Tam giác $OBC$ vuông tại $O$ có $OD$ là đường cao nên $\displaystyle \frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}$

Tam giác $AOD$ vuông tại $O$ có chiều cao $OH$ nên

$\displaystyle \frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}}$ $\displaystyle = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}$ $\displaystyle = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = \frac{{{b^2}{c^2} + {c^2}{a^2} + {a^2}{b^2}}}{{{a^2}{b^2}{c^2}}}$

$\Rightarrow O{H^2} =\displaystyle \frac{{{a^2}{b^2}{c^2}}}{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}}}$

$\Rightarrow OH = \displaystyle \frac{{abc}}{{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}$

Chú ý: Ta thấy khi $OABC$ là tứ diện vuông ($OA, OB, OC$ đôi một vuông góc) thì: $\displaystyle \frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}$.

Từ nay về sau các em sử dụng kết quả này để các bài toán nhanh chóng hơn.

HocTot.Nam.Name.Vn