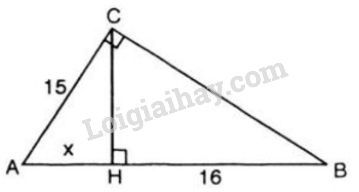
Bài 5 trang 134 SGK Toán 9 tập 2Tam giác ABC vuông tại C có AC = 15cm. Đường cao CH chia AB thành hai đoạn AH và HB. Biết HB = 16cm. Tính diện tích tam giác ABC. Đề bài Tam giác \(ABC\) vuông tại \(C\) có \(AC = 15cm.\) Đường cao \(CH\) chia \(AB\) thành hai đoạn \(AH\) và \(HB.\) Biết \(HB = 16cm.\) Tính diện tích tam giác \(ABC.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Áp dụng hệ thức lượng trong tam giác vuông. +) Diện tích tam giác: \(S=\dfrac{1}{2}h.a\) với \(h\) là chiều cao và \(a\) là cạnh đáy. Lời giải chi tiết
Đặt \(AH = x\) (cm) \((x > 0).\) Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) có đường cao \(CH\) ta có: +) \(AC^2 = AB.AH\) \(\begin{array}{l} +) \(HC^2 = AH. HB = 9. 16 = 144\) \(\Rightarrow\)\(HC=12\) \((cm).\) Vậy diện tích tam giác \(ABC\) là: \(\displaystyle S = {1 \over 2}AB.CH = {1 \over 2}.(16+9).12 = 150(c{m^2}).\)
|