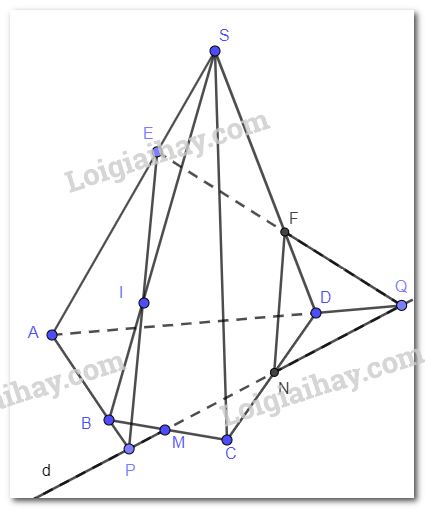
Bài 4.5 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức

Đề bài

Cho hình chóp tứ giác S.ABCD và lấy một điểm E thuộc cạnh SA của hình chóp (E khác S, A).Trong mặt phẳng (ABCD) vẽ một đường thằng d cắt các cạnh CB, CD lần lượt tại M, N và cắt các tia AB, AD lần lượt tại P, Q.

a) Xác định giao điểm của mp (E,d) với các cạnh SB, SD của hình chóp.

b) Xác định giao tuyến của mp (E,d) với các mặt của hình chóp.

Lời giải chi tiết

a) 

- Giao điểm của mp(E,d) với cạnh SB

P thuộc AB suy ra P cũng thuộc mp(SAB)

Trên mp(SAB), gọi giao điểm của EP và SB là I

P thuộc đường thẳng d suy ra P cũng nằm trên mp(E,d)

E, P đều nằm trên mp(D,d) suy ra EP nằm trên mp(E,d) suy ra I cũng nằm trên mp(E,d)

Vậy I là giao điểm của mp(E,d) và SB

- Giao điểm của mp(E,d) với cạnh SD.

Q thuộc AD suy ra Q nằm trên mp(SAD)

Gọi giao điểm của EQ và SD là F

Q thuộc đường thẳng d suy ra Q cũng nằm trên mp(E,d)

E, Q đều nằm trên mp(E,d) suy ra EQ nằm trên mp(E,d) , suy ra F cũng nằm trên mp(E,d)

Vậy F là giao điểm của mp(E,d) và SD.

b) Ta có EI cùng thuộc mp(SAB) và mp(E,d) suy ra EI là tuyến điểm của hai mặt phẳng.

EF cùng thuộc mp(SAD) và mp(E,d) suy ra EF  là giao tuyến của hai mặt phẳng

\(IM \subset mp\left( {SBC} \right),IM \subset mp\left( {E,d} \right)\) suy ra IM là giao tuyến của hai mp(SBC) và mp(E,d).

\(FN \subset mp\left( {SCD} \right),FN \subset mp\left( {E,d} \right)\) suy ra FN là giao tuyến của mp(SCD) và mp(E,d).