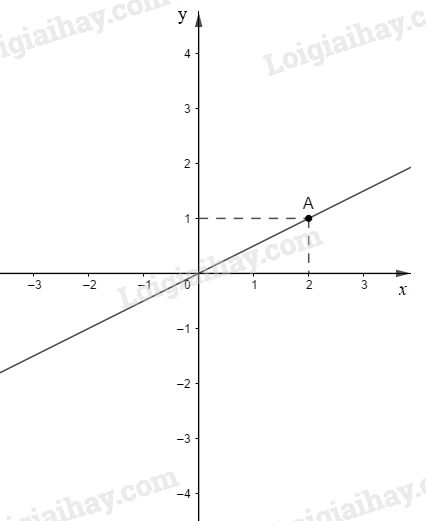
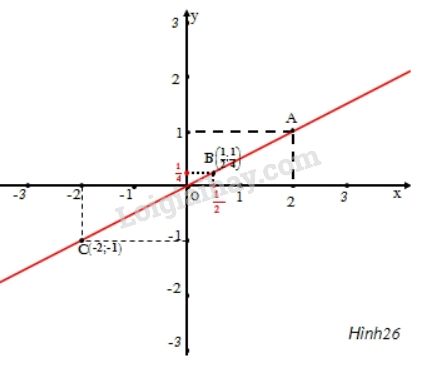
Bài 42 trang 72 SGK Toán 7 tập 1Đường thẳng OA trong hình 26 là đồ thị của hàm số y = ax. Đề bài Đường thẳng OA trong hình 26 là đồ thị của hàm số y=ax. a) Hãy xác định hệ số a. b) Đánh dấu điểm trên đồ thị có hoành độ bằng 12 ; c) Đánh dấu điểm trên đồ thị có tung độ bằng −1.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Để xác định hệ số a, ta thay tọa độ điểm A(2;1) vào hàm số ban đầu sau đó tìm được a. b) Đánh dấu điểm trên đồ thị có hoành độ bằng m: Từ x=m vẽ đường vuông góc với Ox. Giao điểm của đường vuông góc vừa vẽ với đồ thị là điểm cần xác định. c) Đánh dấu điểm trên đồ thị có tung độ bằng n: Từ y=n vẽ đường vuông góc với Oy. Giao điểm của đường vuông góc vừa vẽ với đồ thị là điểm cần xác định. Lời giải chi tiết a) Theo hình vẽ ta có: A(2;1) thuộc vào đồ thị hàm số y=ax Ta thay x=2;y=1 vào hàm số y=ax ta được: 1=a.2⇒a=12 Từ đó ta tìm được hàm số: y=12x b) Điểm trên đồ thị có hoành độ bằng 12. Với x=12 thay vào hàm số: y=12x ta có: y=12.12=14. Vậy điểm cần biểu diễn là B(12;14) * Cách xác định điểm trên đồ thị có hoành độ bằng 12: Từ x=12 vẽ đường vuông góc với Ox. Giao điểm của đường vuông góc vừa vẽ với OA là điểm cần xác định. (Hoặc ta chỉ cần biểu diễn điểm B(12;14) trên mặt phẳng tọa độ) c) Với điểm có tung độ bằng −1 thì ta thay y=−1 vào hàm số y=12x ta được: −1=12.x⇒x=−2 Điểm trên đồ thị có tung độ bằng −1 là điểm C(−2;−1) . * Cách xác định điểm trên đồ thị có tung độ bằng −1: Từ y=−1 vẽ đường vuông góc với Oy. Giao điểm của đường vuông góc vừa vẽ với OA là điểm cần xác định. (Hoặc ta chỉ cần biểu diễn điểm C(−2;−1) trên mặt phẳng tọa độ)
HocTot.Nam.Name.Vn
|