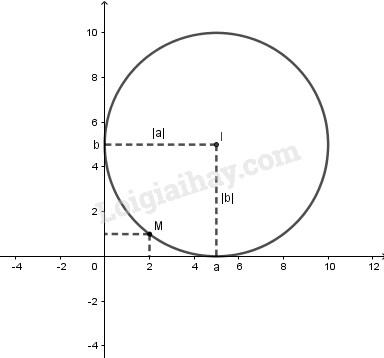
Bài 4 trang 84 SGK Hình học 10

Đề bài

Lập phương trình đường tròn tiếp xúc với hai trục tọa độ $Ox, Oy$ và đi qua điểm $M(2 ; 1).$

Lời giải chi tiết

Gọi đường tròn cần tìm là (C) có tâm $I(a ; b)$ và bán kính bằng R.

(C) tiếp xúc với Ox ⇒ R = d(I ; Ox) = |b|

(C) tiếp xúc với Oy ⇒ R = d(I ; Oy) = |a|

⇒ |a| = |b|

⇒ a = b hoặc a = –b.

Mà (C) đi qua $M(2;1)$ thuộc góc phần tư thứ nhất nên đường tròn nằm hoàn toàn ở góc phần tư thứ nhất hay $a=b>0$

Do đó $R = \left| a \right| = \left| b \right| = a$, phương trình đường tròn cần tìm có dạng:

${\left( {x{\rm{ }} - {\rm{ }}a} \right)^2} + {\left( {y{\rm{ }}-{\rm{ }}a} \right)^2} = {a^2}{\rm{ }}$

$M(2; \, 1)$ thuộc đường tròn nên ta có:

${\left( {2{\rm{ }} - {\rm{ }}a} \right)^2} + {\left( {1{\rm{ }}-{\rm{ }}a} \right)^2} = {a^2}{\rm{ }}$

${a^2} - 6a + 5 = 0 \Leftrightarrow \left[ \matrix{ a = 1 \hfill \cr a = 5 \hfill \cr} \right.(TM)$

Từ đây ta được hai đường tròn thỏa mãn điều kiện

+) Với $a = 1$ $\Rightarrow {\left( {x{\rm{ }} - {\rm{ }}1{\rm{ }}} \right)^2} + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}1} \right)^2}{\rm{ }} = {\rm{ }}1 \, \, ({C_1})$

+) Với $a = 5$ $\Rightarrow {\left( {x - 5{\rm{ }}} \right)^2} + {\rm{ }}{\left( {y - 5} \right)^2}{\rm{ }} = {\rm{ 25}} \, \, ({C_2})$

HocTot.Nam.Name.Vn