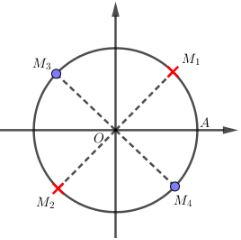
Giải bài 4 trang 29 SGK Đại số và Giải tích 11Giải phương trình Đề bài Giải phương trình 2cos2x1−sin2x=02cos2x1−sin2x=0 Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Tìm ĐKXĐ. +) AB=0⇒A=0AB=0⇒A=0 +) Giải phương trình lượng giác cơ bản: cosx=cosα⇔[x=α+k2πx=−α+k2π(k∈Z) Lời giải chi tiết Điều kiện: sin2x≠1⇔2x≠π2+k2π ⇔x≠π4+kπ(k∈Z) 2cos2x1−sin2x=0 ⇒2cos2x=0 ⇔cos2x=0 ⇔2x=π2+kπ ⇔x=π4+kπ2(k∈Z) Kiểm tra ĐK: π4+kπ2≠π4+lπ ⇔kπ2≠lπ ⇔k2≠l ⇔k≠2l Hay k không thể nhận các giá trị chẵn. Do đó k lẻ nên k=2m+1. Vậy x=π4+(2m+1)π2=3π4+mπ. Vậy phương trình có nghiệm x=3π4+mπ,m∈Z. Chú ý: Nghiệm x=3π4+mπ cũng có thể viết thành x=−π4+nπ bằng cách đặt m=n−1. Các em cũng có thể vẽ đường tròn đơn vị để loại nghiệm như sau: Các điểm biểu diễn x=π4+kπ là M1,M2 nhưng điều kiện là x≠π4+kπ nên hai điểm này không lấy. Các điểm biểu diễn x=π4+kπ2 là M1,M2,M3,M4 nhưng do không lấy hai điểm M1,M2 nên các điểm biểu diễn nghiệm chỉ còn M3,M4. Dễ thấy hai điểm này đối xứng nhau qua O và ^AOM4=−π4 nên nghiệm của phương trình là x=−π4+kπ,k∈Z. HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|