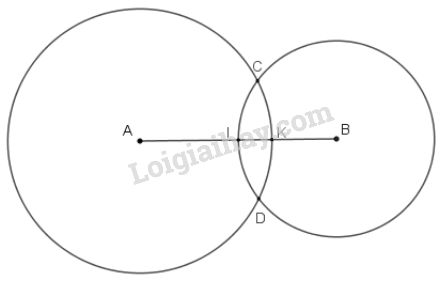
Bài 39 trang 92 SGK Toán 6 tập 2Trên hình 49, ta có hai đường tròn (A;2cm) và (B;2cm) cắt nhau tại C,D, AB=4cm. Đường tròn tâm A,B lần lượt cắt đoạn thẳn AB tại K,I. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn Đề bài Trên hình 49, ta có hai đường tròn và cắt nhau tại Đường tròn tâm lần lượt cắt đoạn thẳn tại
a) Tính b) có phải là trung điểm của đoạn thẳng không? c) Tính Video hướng dẫn giải Phương pháp giải - Xem chi tiết Đường tròn tâm bán kính là hình gồm các điểm cách một khoảng bằng kí hiệu Sử dụng công thức cộng đoạn thẳng: Nếu nằm giữa hai điểm thì Sử dụng: Nếu là trung điểm của đoạn thẳng thì Lời giải chi tiết a) Vì hai đường tròn (A; 3cm) và (B; 2cm) cắt nhau tại C; D nên: Hai điểm và nằm trên đường tròn nên Hai điểm và nằm trên đường tròn nên b) Đường tròn (B; 2cm) cắt đoạn AB tại I nên I nằm trên đường tròn (B; 2cm), suy ra BI = 2cm. Trên tia có: Suy ra nên điểm nằm giữa và (1). Suy ra Do đó: (2) Từ (1) và (2) suy ra là trung điểm của đoạn thẳng c) Đường tròn (A; 3cm) cắt đoạn AB tại K nên K thuộc đường tròn (A ; 3cm) , suy ra AK = 3cm. Trên tia có Vì ( nên điểm nằm giữa hai điểm và Suy ra HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 6 chương trình mới trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 6 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|