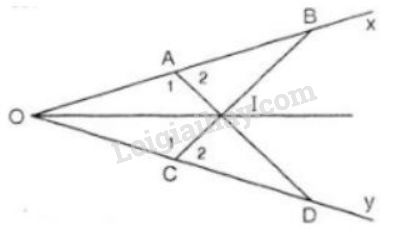
Bài 34 trang 71 SGK Toán 7 tập 2Cho góc xOy khác góc bẹt Đề bài Cho góc khác góc bẹt. Trên tia lấy hai điểm và , trên tia lấy hai điểm và sao cho Gọi là giao điểm của hai đoạn thẳng và Chứng minh rằng: a) b) c) Tia là tia phân giác của góc . Video hướng dẫn giải Phương pháp giải - Xem chi tiết Chứng minh dựa vào các tam giác bằng nhau. Lời giải chi tiết
a) Xét và có: +) (giả thiết) +) (giả thiết) +) là góc chung Vậy (c.g.c) (hai cạnh tương ứng) (điều phải chứng minh). b) Vì (câu a) nên và ( 2 góc tương ứng) Ta có: Hay Ta có: ( góc kề bù)
Xét và ta có: +) (chứng minh trên) +) (chứng minh trên) +) (chứng minh trên) Vậy (g.c.g) và (hai cạnh tương ứng) c) Xét và ta có: +) (giả thiết) +) (chứng minh trên) +) (chứng minh trên) Vậy (c.g.c) ( 2 góc tương ứng) là phân giác của .
|