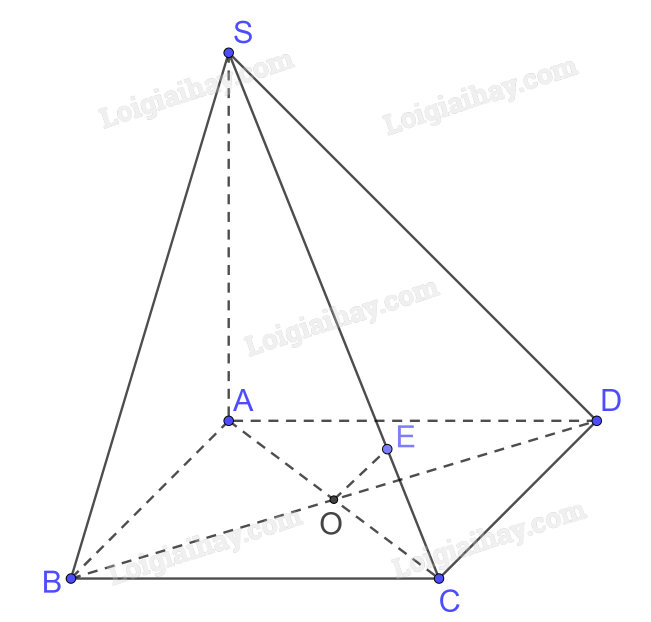
Bài 34 trang 109 SGK Toán 11 tập 2 - Kết nối tri thứcCho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và (widehat {BAD} = {60^0}). Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và \(\widehat {BAD} = {60^0}\). Biết \(SA \bot (ABCD)\) và \(SA = a\). a) Chứng minh rằng \(BD \bot SC\). b) Tính theo a khoảng cách giữa hai đường thẳng BD và SC. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Nếu đường vuông góc chung \(\Delta \) cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b. Lời giải chi tiết
a) Ta có \(BD \bot AC,BD \bot SA \Rightarrow BD \bot \left( {SAC} \right);SC \subset \left( {SAC} \right) \Rightarrow BD \bot SC\) b) Trong (SAC) kẻ \(OE \bot SC\) Mà \(BD \bot \left( {SAC} \right) \Rightarrow OE \bot BD\) \( \Rightarrow d\left( {BD,SC} \right) = OE\) Gọi \(AC \cap BD = \left\{ O \right\}\) Xét tam giác BAD có AB = AD, \(\widehat {BAD} = {60^0}\) \( \Rightarrow \) Tam giác BAD đều \( \Rightarrow AO = \frac{{a\sqrt 3 }}{2} \Rightarrow AC = a\sqrt 3 \) Xét tam giác SAC vuông tại A có \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}} = 2a\) Dễ dàng chứng minh được \( \Rightarrow \frac{a}{{OE}} = \frac{{2a}}{{\frac{{a\sqrt 3 }}{2}}} \Rightarrow OE = \frac{{a\sqrt 3 }}{4}\) Vậy \(d\left( {BD,SC} \right) = \frac{{a\sqrt 3 }}{4}\)
|