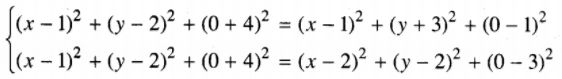Bài 31 trang 121 Sách bài tập Hình học lớp 12 Nâng caoa)Viết phương trình mặt cầu đi qua
Lựa chọn câu để xem lời giải nhanh hơn
LG a Viết phương trình mặt cầu đi qua A(1;2;-4), B(1;-3;1), C(2;2;3) và có tâm nằm trên mp(Oxy). Lời giải chi tiết: Gọi I là tâm mặt cầu. Vì \(I \in mp(Oxy)\) nên I=(x;y;0). Theo giả thiết, ta có \(A{I^2} = B{I^2} = C{I^2}\), suy ra
\(\Rightarrow \left\{ \matrix{ x = - 2 \hfill \cr y = 1 \hfill \cr} \right. \Rightarrow I( - 2;1;0). \) Bán kính của mặt cầu là: \(R = AI = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left( {1 - 2} \right)}^2} + {4^2}} = \sqrt {26} \) Vậy phương trình mặt cầu là: \({(x + 2)^2} + {(y - 1)^2} + {z^2} = 26.\) LG b Viết phương trình mặt cầu đi qua hai điểm A(3;-1;2), B(1;1;-2) và có tâm thuộc trục Oz. Lời giải chi tiết: Gọi I là tâm mặt cầu, \(I \in Oz\) nên I = (0;0;z). Theo giả thiết \(A{I^2} = B{I^2}\), ta có phương trình \({( - 3)^2} + {1^2} + {(z - 2)^2} = {( - 1)^2} + {( - 1)^2} + {(z + 2)^2}\) \(\Rightarrow 8z = 8 \Rightarrow z = 1\) Vậy \(I=(0;0;1)\) và \(AI = \sqrt {11} .\) Phương trình mặt cầu cần tìm là \({x^2} + {y^2} + {(z - 1)^2} = 11\) LG c Viết phương trình mặt cầu đi qua bốn điểm A(1;1;1), B(1;2;1), C(1;1;2), D(2;2;1). Lời giải chi tiết: Phương trình mặt cầu (S) cần tìm có dạng Ta có : \(\eqalign{ & {(x)^2} + {(y)^2} + {(z)^2} - 2ax - 2by - 2cz + d = 0 \cr & A \in (S) \Leftrightarrow 2a + 2b + 2c - d = 3. \cr & B \in (S) \Leftrightarrow 2a + 4b + 2c - d = 6. \cr & C \in (S) \Leftrightarrow 2a + 2b + 4c - d = 6. \cr & D \in (S) \Leftrightarrow 4a + 4b + 2c - d = 9. \cr} \) Từ đó ta suy ra \(a = {3 \over 2};b = {3 \over 2};c = {3 \over 2};d = 6.\) Vậy phương trình mặt cầu là : \({x^2} + {y^2} + {z^2} - 3x - 3y - 3z + 6 = 0.\) HocTot.Nam.Name.Vn
|