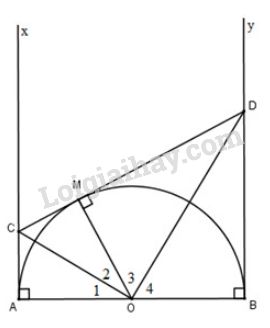
Bài 30 trang 116 SGK Toán 9 tập 1Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn) Đề bài Cho nửa đường tròn tâm \(O\) có đường kính \(AB\) (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi \(Ax,\ By\) là các tia vuông góc với \(AB\) (\(Ax,\ By\) và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ \(AB\)). Qua điểm \(M\) thuộc nửa đường tròn (\(M\) khác \(A\) và \(B\)), kẻ tiếp tuyến với nửa đường tròn, nó cắt \(Ax\) và \(By\) theo thứ tự ở \(C\) và \(D\). Chứng minh rằng: a) \(\widehat {CO{\rm{D}}} = {90^0}\) b) \(CD=AC+BD\) c) Tích \(AC.BD\) không đổi khi điểm \(M\) di chuyển trên nửa đường tròn. Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Sử dụng tính chất hai đường tiếp tuyến cắt nhau: \(AB,\ AC\) là tiếp tuyến của \((O)\) tại \(A,\ B\) thì 1) \(AB=AC\); 2) \(OA\) là tia phân giác của góc \(\widehat{BOC}\). +) Sử dụng hệ thức lượng trong tam giác vuông: \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\). Khi đó \(AH^2=HB.HC\) Lời giải chi tiết
Ta có: \(OA\perp Ax\) (gt) \(OB\perp By\) (gt) \(\Rightarrow\) \(Ax,\ By\) là các tiếp tuyến của đường tròn lần lượt tại \(A,\ B\). Vì \(CA,\ CM\) là hai tiếp tuyến của \((O)\) lần lượt tại \(A\) và \(M\), theo tính chất hai tiếp tuyến cắt nhau, ta có: \(CM =CA\) và \(\widehat{O_1}=\widehat{O_2}\) Vì \(DB,\ DM\) là hai tiếp tuyến của \((O)\) lần lượt tại \(B\) và \(M\), theo tính chất hai tiếp tuyến cắt nhau, ta có: \(DM=DB\) và \(\widehat{O_3}=\widehat{O_4}\) a) Ta có: \(\eqalign{ b) Ta có: \(CM=AC,\ MD=BD\) (chứng minh trên) Lại có: \(CD=CM+MD=AC+BD\) (đpcm) c) Ta có: \(CM=AC,\ MD=BD\) (chứng minh trên) Xét tam giác \(COD\) vuông tại \(O\), áp dụng hệ thức lượng trong tam giác vuông, ta có: \(MO^2=MC.MD=AC.BD=R^2\) Vì bán kính đường tròn không đổi khi \(M\) di chuyển trên nửa đường tròn nên \(MO^2\) không đổi do đó tích \(AC.BD\) không đổi khi \(M\) di chuyển trên nửa đường tròn.
|