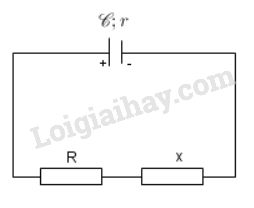
Bài 3 trang 62 SGK Vật lí 11

Đề bài

Cho mạch điện có sơ đồ như hình 11.5, trong đó nguồn điện có suất điện động ξ = 12V, và điện trở trong là r = 1,1 Ω; điện trở R = 0,1 Ω. 

 

a) Điện trở x phải có trị số bao nhiêu để công suất tiêu thụ ở ngoài mạch là lớn nhất?

b) Điện trở x phải có trị số bao nhiêu để công suất tiêu thụ ở điện trở này là lớn nhất? Tính công suất lớn nhất đó.

Lời giải chi tiết

a) Tính điện trở x để công suất tiêu thụ ở mạch ngoài là lớn nhất.

- Mạch ngoài gồm điện trở R mắc nối tiếp với điện trở x, có điện trở tương đương là: R_N = R + x = 0,1 + x.

- Cường độ dòng điện trong trong mạch : \(I{\rm{ }} = \displaystyle{\rm{ }}{\xi  \over {R{\rm{ }} + {\rm{ }}r{\rm{ }} + {\rm{ }}x}}\)

- Công suất tiêu thụ mạch ngoài:

 \(P = {I^2}{R_N} = \displaystyle{{{\xi ^2}(R + x)} \over {{{\left( {R + r + x} \right)}^2}}} \\= {{{\xi ^2}} \over {{{\left( {\sqrt {R + x}  + \displaystyle{r \over {\sqrt {R + x} }}} \right)}^2}}}\)

Để công suất P trên đây lớn nhất thì mẫu số ở về phải là nhỏ nhất. 

Xét biểu thức:

 \(Y = {\left( {\sqrt {R + x}  + \dfrac{r}{{\sqrt {R + x} }}} \right)^2} \\= \left( {R + x + \dfrac{{{r^2}}}{{R + x}} + 2r} \right)\)

Ta có \({Y_{\min }}\) khi \(A = {\left[ {R + x + \dfrac{{{r^2}}}{{R + x}}} \right]_{\min }}\)

Áp dụng BĐT Cosi cho A, ta có: \(A = {\left[ {R + x + \dfrac{{{r^2}}}{{R + x}}} \right]_{\min }} \ge 2\sqrt {\left( {R + x} \right)\dfrac{{{r^2}}}{{\left( {R + x} \right)}}} \\ = 2r\)

Vậy \({A_{\min }}\) (hay \({Y_{\min }}\))  khi \(R + x = \dfrac{{{r^2}}}{{R + x}}\) hay \(R + x = r\)

Vậy \({P_{{\mathop{\rm ma}\nolimits} x}}\) khi \(R + x = r \Rightarrow x = r - R = 1,1 - 0,1 = 1\Omega \)

b) Công suất tiêu thụ trên điện trở x: 

\({P_x} = {I^2}x = \dfrac{{{\xi ^2}}}{{{{\left( {R + r + x} \right)}^2}}}x\\ = \dfrac{{{\xi ^2}}}{{\dfrac{{{{\left( {R + r} \right)}^2}}}{x} + 2\left( {R + r} \right) + x}}\)

Để công suất \(P_x\) trên đây lớn nhất thì mẫu số ở về phải là nhỏ nhất. 

Xét biểu thức:  

\(J = \dfrac{{{{\left( {R + r} \right)}^2}}}{x} + 2\left( {R + r} \right) + x\)

Ta có \({J_{\min }}\) khi \(B = {\left[ {\dfrac{{{{\left( {R + r} \right)}^2}}}{x} + x} \right]_{\min }}\)

Áp dụng BĐT Cosi cho B, ta có:

\(B = {\left[ {\dfrac{{{{\left( {R + r} \right)}^2}}}{x} + x} \right]_{\min }} \ge 2\sqrt {\dfrac{{{{\left( {R + r} \right)}^2}}}{x}x} \\ = 2\left( {R + r} \right)\)

Vậy \({B_{\min }}\) (hay \({J_{\min }}\))  khi

\(\dfrac{{{{\left( {R + r} \right)}^2}}}{x} = x\) hay \(R + r = x\)

Vậy \({P_{{x_{{\mathop{\rm ma}\nolimits} x}}}}\) khi \(x = R + r = 0,1 + 1,1 = 1,2\Omega \)

Giá trị của công suất lớn nhất này là: \(30 W\)

HocTot.Nam.Name.Vn