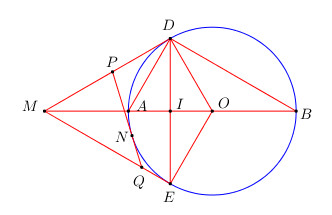
Bài 3 trang 148 Tài liệu dạy – học Toán 9 tập 1

Đề bài

Cho đường tròn (O) đường kính AB = 2R. Vẽ dây DE vuông góc với AO tại I là trung điểm của AO.

a) Chứng minh rằng tam giác ADB vuông. Tính AD, DB theo R.

b) Tiếp tuyến với đường tròn (O) tại D cắt đường thẳng AB tại M. Chứng minh rằng ME là tiếp tuyến của đường tròn (O).

c) Chứng minh rằng : MA.MB = MI.MO.

d) Trên đường tròn (O) lấy điểm N ( N nằm trên nửa mặt phẳng bờ DE chứa điểm A và $N \ne A$). Tiếp tuyến với (O) tại N cắt MD ở P và cắt ME ở Q. Trường hợp cho $\widehat {DME} = {60^o}$, tính theo R chu vi tam giác MPQ.

Lời giải chi tiết

 

a) Ta có $\widehat {ADB}$ chắn nửa đường tròn đường kính $AB \Rightarrow \widehat {ADB} = {90^0}$.

Do đó tam giác $ADB$ vuông tại $D$.

Áp dụng hệ thức lượng trong tam giác vuông ADB có: $A{D^2} = AB.AI = 2R.\dfrac{R}{2} = {R^2}$ $\Leftrightarrow AD = R$.

Áp dụng định lí Pytago trong tam giác vuông ADB có:

$D{B^2} = A{B^2} - A{D^2} = {\left( {2R} \right)^2} - {R^2} = 3{R^2}$ $\Rightarrow DB = R\sqrt 3$.

b) Xét tam giác vuông ODI và tam giác vuông OEI có:

$OI\,\,chung$

$ID = IE$ (quan hệ vuông góc giữa đường kính và dây cung)

$\Rightarrow \Delta ODI = \Delta OEI$ (cạnh huyền – cạnh góc vuông)

$\Rightarrow \angle DOI = \angle EOI$ hay $\angle MOD = \angle MOE$.

Xét $\Delta OMD$ và $\Delta OME$ có :

$\begin{array}{l}OM\,\,chung;\\\angle MOD = \angle MOE\,\,\left( {cmt} \right)\\OD = OE = R\\ \Rightarrow \Delta OMD = \Delta OME\,\,\left( {c.g.c} \right)\\ \Rightarrow \angle MEO = \angle MDO = {90^0}\end{array}$

Mà $OE$ là bán kính của $\left( O \right) \Rightarrow ME$ là tiếp tuyến của $\left( O \right)$ tại $E$.

c) Ta có : $\angle ADM + \angle ADO = \angle MDO = {90^0}$

$OA = OD = AD = R \Rightarrow \Delta OAD$ đều $\Rightarrow \angle ODA = \angle OAD = {60^0}$

Xét tam giác vuông ABD có : $\angle OAD + \angle ABD = {90^0}$

$\Rightarrow \angle ADM = \angle ABD$.

Xét $\Delta ADM$ và $\Delta DBM$ có :

$\begin{array}{l}\angle BMD\,\,chung\\\angle ADM = \angle ABD\,\,\left( {cmt} \right)\\ \Rightarrow \Delta ADM \sim \Delta DBM\,\,\left( {g.g} \right) \\\Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MD}}{{MB}} \\\Rightarrow M{D^2} = MA.MB\,\,\left( 1 \right)\end{array}$

Áp dụng hệ thức lượng trong tam giác vuông ODM có : $M{D^2} = MI.MO\,\,\left( 2 \right)$

Từ (1) và (2) $\Rightarrow MA.MB = MI.MO$.

d) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có : $PD = PN;\,\,QE = QN$

Ta có : Chu vi tam giác MPQ là:

${C_{\Delta MPQ}} = MP + MQ + PQ$$\,= MP + MQ + PN + QN = MD + ME$.

Mà $MD = ME$ (tính chất 2 tiếp tuyến cắt nhau). Lại có $\angle DME = {60^0}$ $\Rightarrow \Delta MDE$ đều

$\Rightarrow MD = ME = DE$ $\Rightarrow {C_{\Delta MPQ}} = 2DE = 4DI$.

Áp dụng hệ thức lượng trong tam giác vuông ABD ta có :

$D{I^2} = AI.BI = \dfrac{R}{2}.\dfrac{{3R}}{2} = \dfrac{{3{R^2}}}{4}\\ \Rightarrow DI = \dfrac{{R\sqrt 3 }}{2}$.

Vậy khi $\angle DME = {60^0}$ thì ${C_{\Delta MPQ}} = 4.\dfrac{{R\sqrt 3 }}{2} = 2R\sqrt 3$.

 HocTot.Nam.Name.Vn