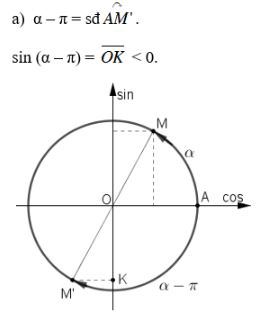
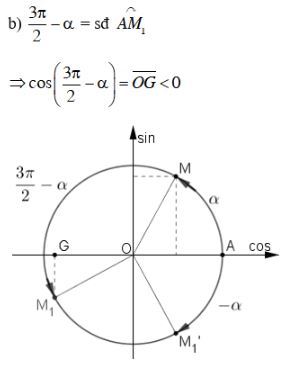
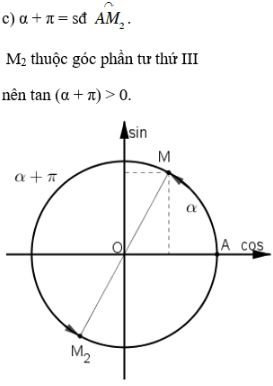
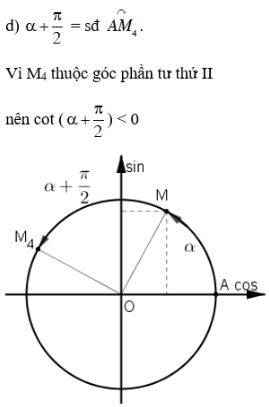
Bài 3 trang 148 SGK Đại số 10

LG a

\(\sin(α - π)\);

Phương pháp giải:

Áp dụng các công thức đặc biệt:

\(\sin \left( {\pi - x } \right) = \sin x \) và \(\sin \left( { - x } \right) =  - \sin x \)

Lời giải chi tiết:

Với \(0 < α < \dfrac{\pi}{2}\) ta có: \(\sin \alpha  > 0,\cos \alpha  > 0,\) \(\tan\alpha  > 0,\cot \alpha  > 0.\)

\(\sin \left( {\alpha  - \pi } \right)\)

\( = \sin \left[ { - \left( {\pi  - \alpha } \right)} \right]\)

\( =  - \sin \left( {\pi  - \alpha } \right) \)

(áp dụng \(\sin \left( { - x } \right) =  - \sin x \) với \(x = \pi  - \alpha \))

\(=  - \sin \alpha \)

(áp dụng \(\sin \left( {\pi - x } \right) = \sin x \) với \(x=\alpha\))

Mà \(\sin \alpha  > 0\) nên \( - \sin \alpha  < 0\) hay \(\sin \left( {\alpha  - \pi } \right) < 0\).

Cách khác

LG b

\(\cos\left( \dfrac{3\pi }{2}- α\right)\)

Phương pháp giải:

Áp dung các công thức đặc biệt:

\(\cos \left( {\pi  + \alpha } \right) =  - \cos \alpha \) và \(\cos \left( {\dfrac{\pi }{2} - \alpha } \right) = \sin \alpha \)

Lời giải chi tiết:

Ta có: \(\cos \left( {\dfrac{{3\pi }}{2} - \alpha } \right) \)

\(= \cos \left( {\pi  + \dfrac{\pi }{2} - \alpha } \right) \)

\(=  - \cos \left( {\dfrac{\pi }{2} - \alpha } \right) \)

(áp dụng \(\cos \left( {\pi  + x} \right) =  - \cos x\) với \(x = \frac{\pi }{2} - \alpha \))

\(=  - \sin\alpha  .\)

(áp dụng \(\cos \left( {\frac{\pi }{2} - x} \right) = \sin x\) với \(x=\alpha \))

Mà \(\sin\alpha >0\) nên \(- \sin\alpha  <0\) hay \(\cos \left( {\dfrac{{3\pi }}{2} - \alpha } \right) <0\).

Cách khác:

LG c

\(\tan(α + π)\);

Phương pháp giải:

Áp dụng công thức đặc biệt: \(\tan \left( {\alpha + \pi } \right) = \tan \alpha\)

Lời giải chi tiết:

Ta có: \(\tan \left( {\alpha + \pi } \right) = \tan \alpha .\)

Mà \(\tan α > 0\) nên \(\tan (α + π) > 0\).

Cách khác:

LG d

\(\cot\left(α +  \dfrac{\pi }{2}\right)\)

Phương pháp giải:

Áp dụng các công thức đặc biệt: \(\cot \left( {\dfrac{\pi }{2} - \alpha } \right) = \tan \alpha \) và \(\tan \left( { - \alpha } \right) =  - \tan \alpha \)

Lời giải chi tiết:

\(\cot \left( {\dfrac{\pi }{2} + \alpha } \right) = \cot \left[ {\dfrac{\pi }{2} - \left( { - \alpha } \right)} \right]\) \( = \tan \left( { - \alpha } \right) =  - \tan \alpha \)

Mà \(\tan \alpha  > 0\) nên \( - \tan \alpha  < 0\) hay \(\cot \left( {\dfrac{\pi }{2} + \alpha } \right) < 0\).

Cách khác:

HocTot.Nam.Name.Vn