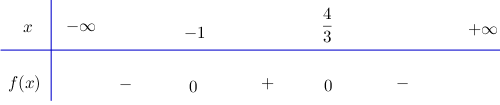
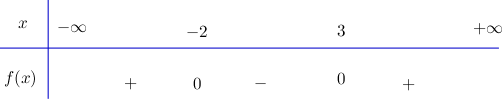
Bài 3 trang 105 SGK Đại số 10Giải các bất phương trình sau... Video hướng dẫn giải Giải các bất phương trình sau LG a 4x2−x+1<0; Phương pháp giải: Sử dụng cách xét dấu của nhị thức bậc nhất và tam thức bậc hai để giải bất phương trình. Lời giải chi tiết: Tam thức f(x)=4x2−x+1<0 có hệ số a=4>0 biệt thức ∆=(−1)2−4.4.1=−15<0. Do đó f(x)>0,∀x∈R. Vậy bất phương trình 4x2−x+1<0 vô nghiệm. Cách khác: 4x2−x+1 =(2x)2−2.2x.14+116+1516 =(2x−14)2+1516≥1516>0,∀x∈R Do đó bpt 4x2−x+1<0 vô nghiệm. LG b −3x2+x+4≥0; Lời giải chi tiết: −3x2+x+4≥0 Ta xét: f(x)=−3x2+x+4=0 ⇔[x=−1x=43 Ta có bảng xét dấu: Do đó: −3x2+x+4≥0⇔−1≤x≤43. LG c 1x2−4<33x2+x−4; Lời giải chi tiết: 1x2−4<33x2+x−4 ⇔1x2−4−33x2+x−4<0 ⇔3x2+x−4−3x2+12(x2−4)(3x2+x−4)<0 ⇔x+8(x2−4)(3x2+x−4)<0 Lập bảng xét dấu vế trái: + Nhị thức x+8 có nghiệm x=−8 + Tam thức x2–4 có hai nghiệm x=2 và x=−2, hệ số a=1>0 Do đó x2–4 mang dấu + khix<−2 hoặc x>2 và mang dấu – khi −2<x<2. + Tam thức 3x2+x–4 có hai nghiệm x=1 và x=−4/3, hệ số a=3>0 Do đó 3x2+x–4 mang dấu + khi x<−4/3 hoặc x>1, mang dấu – khi −4/3<x<1. Bảng xét dấu: Tập nghiệm của bất phương trình S=(−∞;−8)∪(−2;−43)∪(1;2). LG d x2−x−6≤0. Lời giải chi tiết: x2−x−6≤0 x2−x−6=0 ⇔[x=3x=−2 Ta có bảng xét dấu: Tập nghiệm của bất phương trình là: S=[−2;3]. HocTot.Nam.Name.Vn
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|