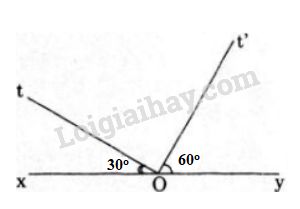
Bài 29 trang 85 SGK Toán 6 tập 2Gọi Ot, Ot' là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng xy ... Đề bài Gọi \(Ot, Ot'\) là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng \(xy\) đi qua \(O.\) Biết \(\widehat{xOt}=30^0,\) \(\widehat{yOt'}=60^0.\) Tính số đo các góc \(yOt, tOt'.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\). Trên nửa mặt phẳng bờ chứa tia \(Ox\) có hai tia \(Oy, Oz\) mà \(\widehat{xOy}< \widehat{xOz}\) thì tia \(Oy\) nằm giữa hai tia \(Ox, Oz.\) Hai góc kề bù thì có tổng số đo bằng 180 độ. Lời giải chi tiết Vì \(Ox\) và \(Oy\) là hai tia đối nhau nên \(\widehat{xOy}=180^0\) (góc bẹt) Ta có \(Ot\) nằm trên nửa mặt phẳng có bờ là đường thẳng \(xy\), \(\widehat{xOt}=30^0\) Vì \(\widehat{xOt}<\widehat{xOy}\) (vì \(30^0<180^0)\) nên tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\) Suy ra \(\widehat{xOt}+\widehat{yOt}=\widehat{xOy}\) Do đó \(\widehat{yOt}=\widehat{xOy}-\widehat{xOt}\) \(= 180^0-30^0=150^0 \) Hai tia \(Ot'\) và \(Ot\) cùng thuộc nửa mặt phẳng bờ \(Oy\) mà \(\widehat{yOt'}<\widehat{yOt}\) (vì \(60^0<150^0)\) nên tia \(Ot'\) nằm giữa hai tia \(Oy\) và \(Ot.\) Suy ra \(\widehat{yOt'}+\widehat{t'Ot}=\widehat{tOy}\) Thay số ta được: \(60^0+\widehat{t'Ot}=150^0\) Suy ra: \(\widehat{t'Ot}=150^0-60^0=90^0\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
