Bài 29 trang 59 SBT Hình học 12 Nâng caoGiải bài 29 trang 59 sách bài tập Hình học 12 Nâng cao. Xét hình trụ nội tiếp một mặt cầu bán kính R ...
Lựa chọn câu để xem lời giải nhanh hơn
Xét hình trụ nội tiếp một mặt cầu bán kính R mà diện tích thiết diện qua trục hình trụ là lớn nhất. Tính : LG 1 Thể tích V và diện tích toàn phần \({S_{tp}}\) của hình trụ. Lời giải chi tiết:
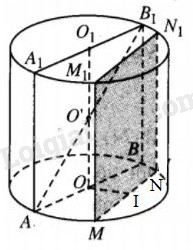
Gọi O’ là trung điểm của trục \({O_1}O\) của hình trụ thì O’ là tâm mặt cầu đã cho. Kí hiệu h và r lần lượt là chiều cao và bán kính đáy của hình trụ thì diện tích thiết diện qua trục là \({S_{td}} = 2r.h.\) Mặt khác \({R^2} = O'{A^2} = {r^2} + {{{h^2}} \over 4} \Rightarrow {r^2} = {R^2} - {{{h^2}} \over 4}.\) Từ đó \({S_{td}} = h\sqrt {4{R^2} - {h^2}} = \sqrt {{h^2}(4{R^2} - {h^2})} .\) Vậy \({S_{td}}\) lớn nhất khi và chỉ khi \(h = R\sqrt 2 .\) Khi đó \(r = \sqrt {{R^2} - {1 \over 4}.2{R^2}} = {{R\sqrt 2 } \over 2} = {h \over 2},\) tức là thiết diện qua trục là hình vuông. \(V = \pi {r^2}h = 2\pi {r^2}.r = 2\pi {r^3} = {{\pi {R^3}\sqrt 2 } \over 2}.\) \({S_{tp}} = 2\pi {r^2} + 2\pi rh = 3\pi {R^2}.\) LG 2 Thể tích hình lăng trụ n-giác đều nội tiếp hình trụ và thể tích hình lăng trụ n-giác đều ngoại tiếp hình trụ. Lời giải chi tiết: \( \bullet \) Dễ thấy diện tích đáy của hình lăng trụ n-giác đều nội tiếp hình trụ là \({n \over 2}{r^2}\sin {{2\pi } \over n}\). Vậy thể tích hình lăng trụ đó là: \(V_{\text{lăng trụ}}={n \over 2}{r^2}\sin {{2\pi } \over n}.2r = n{r^3}\sin {{2\pi } \over n} \) \(= {{n{R^3}} \over {2\sqrt 2 }}\sin {{2\pi } \over n}\) \( \bullet \) Xét đa giác đều n cạnh ngoại tiếp đường tròn đáy hình trụ thì độ dài cạnh của đa giác bằng \(2r\tan {\pi \over n},\) từ đó diện tích đáy hình trụ là \({S_{đáy}} = n.{1 \over 2}2r.\tan {\pi \over n}.r = n{r^2}\tan {\pi \over n}.\) Vậy thể tích hình lăng trụ n-giác đều ngoại tiếp hình trụ là \(n{r^2}\tan {\pi \over n} \cdot 2r = 2n{r^3}.\tan {\pi \over n} \) \(= {{n{R^3}} \over {\sqrt 2 }}\tan {\pi \over n}\) LG 3 Diện tích thiết diện của hình trụ khi cắt bởi một mặt phẳng song song với trục hình trụ và cách trục một khoảng \({R \over 2}.\) Lời giải chi tiết: Giả sử thiết diện là \(MN{N_1}{M_1}\) thì \(MN{N_1}{M_1}\) là hình chữ nhật. Gọi I là trung điểm của MN thì \(OI = {R \over 2}\) và \(IM = \sqrt {{r^2} - {{{R^2}} \over 4}} = \sqrt {{{{R^2}} \over 2} - {{{R^2}} \over 4}} = {R \over 2}.\) Vậy diện tích thiết diện \(MN{N_1}{M_1}\) là \(MN.N{N_1} = 2IM.h = R.R\sqrt 2 = {R^2}\sqrt 2 .\) HocTot.Nam.Name.Vn
|