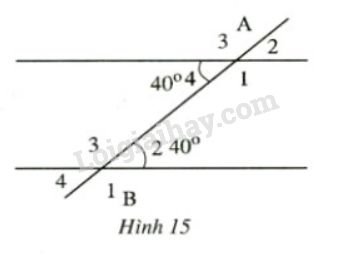
Bài 22 trang 89 SGK Toán 7 tập 1

Đề bài

a) Vẽ lại hình 15.

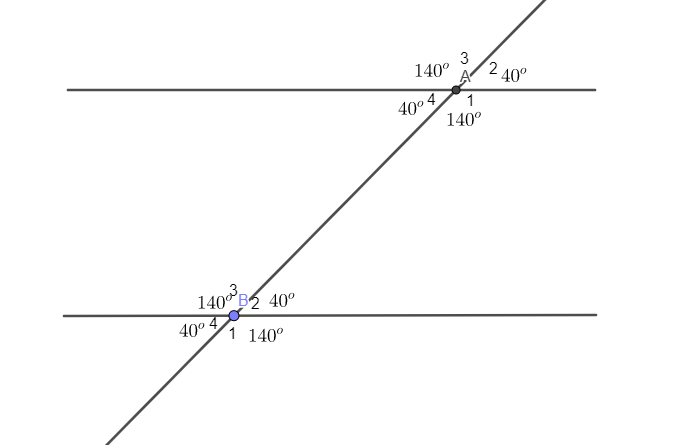
b) Ghi tiếp số đo ứng với các góc còn lại.

c) Cặp góc $A_{1},B_{2}$ và cặp góc $A_{4},B_{3}$ được gọi là hai cặp góc trong cùng phía.

Tính:

$\widehat{A_{1}}+\widehat{B_{2}}; \widehat{A_{4}}+\widehat{B_{3}}$.

Lời giải chi tiết

a) Vẽ lại hình.

b) $\widehat {{A_2}} = \widehat {{A_4}}$ (Hai góc đối đỉnh) 

$\Rightarrow \widehat {{A_2}} = {40^o}$

$\eqalign{ & \widehat {{A_1}} + \widehat {{A_4}} = {180^o}(\text{ hai góc kề bù }) \cr & \Rightarrow \widehat {{A_1}} = {180^0} - \widehat {{A_4}} \cr&\;\;\;\;\;\;\;\;\;\;= {180^o} - {40^o} = {140^o} \cr}$

$\eqalign{ & \widehat {{A_1}} = \widehat {{A_3}}(\text{ hai góc đối đỉnh }) \cr & \Rightarrow \widehat {{A_3}} = {140^o} \cr}$

$\eqalign{ & \widehat {{B_2}} = \widehat {{B_4}}(\text{ hai góc đối đỉnh }) \cr & \Rightarrow \widehat {{B_4}} = {40^o} \cr}$

$\eqalign{ & \widehat {{B_2}} + \widehat {{B_3}} = {180^o} (\text{ hai góc kề bù })\cr & \Rightarrow \widehat {{B_3}} = {180^o} - \widehat {{B_2}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^o} - {40^o} = {140^o} \cr}$

$\eqalign{ & \widehat {{B_3}} = \widehat {{B_1}}(\text{ hai góc đối đỉnh }) \cr  & \Rightarrow \widehat {{B_1}} = {140^o} \cr}$

Ghi số đo ứng với các góc còn lại ta được hình bên:

c) Ta có:

$\widehat{A_{1}}+\widehat{B_{2}}=140^{\circ}+40^{\circ}=180^{\circ}$

$\widehat{A_{4}}+\widehat{B_{3}}=40^{\circ}+140^{\circ}=180^{\circ}$.

HocTot.Nam.Name.Vn