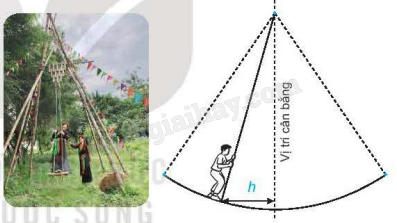
Bài 22 trang 107 SGK Toán 11 tập 2 - Kết nối tri thức

Đề bài

Mùa xuân ở hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún cây đu sẽ đưa người chơi dao động qua lại quanh vị tri cân bằng. Giả sử khoảng cách \(h\) (tính bằng mét) từ người chơi đu đến vị trí cân bằng được tính theo thời gian \(t(t \ge 0\) và được tính bằng giây) bởi hệ thức \(h = |d|\) với \(d = 3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right]\), trong đó ta quy ước rằng \(d > 0\) khi vị trí cân bằng ở về phía sau lưng người chơi đu và \(d < 0\) trong trường hợp ngược lại.

a) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất.

b) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu cách vị trí cân bằng 2 m (tính chính xác đến 0,01 giây).

 

Lời giải chi tiết

a) Ta có \(h = \left| d \right| = 3\left| {\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right| \le 3.\) Vậy người chơi đu ở xa vị trí cân bằng nhất khi \(\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] =  \pm 1 \Leftrightarrow \sin \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0 \Leftrightarrow \frac{\pi }{3}\left( {2t - 1} \right) = k\pi  \Leftrightarrow t = \frac{1}{2} + \frac{3}{2}k,k \in \mathbb{Z}.\)

Với \(t \in \left[ {0;2} \right]\) nên k = 0 và k = 1. Vậy trong vòng 2 giây đầu tiên, người chơi đu ở xa vị trí cân bằng nhất tại các thời điểm t = 0,5 giây và t = 2 giây.

b) Người chơi đu cách vị trí cân bằng 2 m khi

\(h = 2 \Leftrightarrow 3\left| {\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right| = 2 \Leftrightarrow {\cos ^2}\left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \frac{4}{9} \Leftrightarrow \cos \left[ {\frac{{2\pi }}{3}\left( {2t - 1} \right)} \right] = \frac{{ - 1}}{9}.\)

Suy ra \(t = \frac{1}{2} \pm \frac{3}{{4\pi }}\arccos \left( {\frac{{ - 1}}{9}} \right) + \frac{{3k}}{2},k \in \mathbb{Z}.\) Vì \(t \in \left[ {0;2} \right]\) nên \(t \approx 0,1\) giây; \(t \approx 0,9\) giây và \(t \approx 1,6\) giây.