Đề bài
Cho hình hộp ABCD.A′B′C′D′. Chứng minh rằng:
a) −−→AB + −−−→B′C′ + −−→DD′ = −−→AC′;
b) −−→BD - −−→D′D - −−−→B′D′ = −−→BB′;
c) −−→AC + −−→BA′ + −−→DB + −−→C′D = →0.
Video hướng dẫn giải
Dựa vào các vector bằng nhau và quy tắc ba điểm.
Lời giải chi tiết
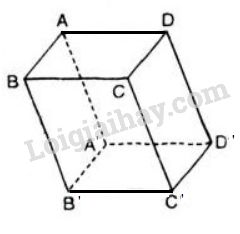
a) Ta có: −−−→B′C′=−−→BC;−−→DD′=−−→CC′
−−→AB + −−−→B′C′ + −−→DD′
= −−→AB + −−→BC + −−→CC′
=−−→AC+−−→CC′
= −−→AC′;
b) −−→BD - −−→D′D - −−−→B′D′
= −−→BD + −−→DD′ + −−−→D′B′
=−−→BD′+−−−→D′B′
= −−→BB′;
c) Ta có: BA′D′C là hình bình hành ⇒−−→BA′=−−→CD′
BDD′B′ là hình bình hành ⇒−−→DB=−−−→D′B′
AB′C′D là hình bình hành ⇒−−→C′D=−−→B′A
−−→AC + −−→BA′ + −−→DB + −−→C′D
= −−→AC + −−→CD′ + −−−→D′B′ + −−→B′A
=−−→AD′+−−−→D′B′+−−→B′A
=−−→AB′+−−→B′A
= →0.
HocTot.Nam.Name.Vn













