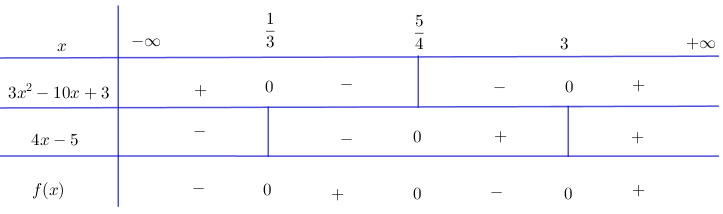
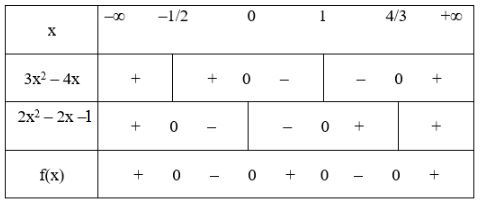
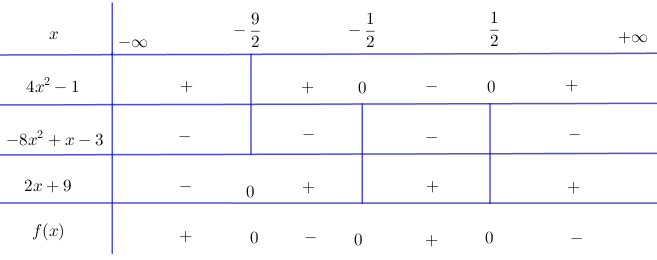
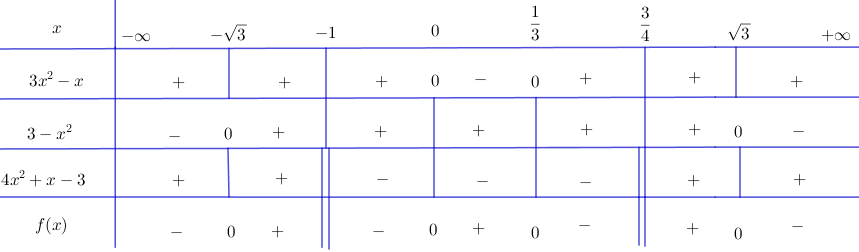
Bài 2 trang 105 SGK Đại số 10

LG a

\(f(x) =(3{x^2} - 10x + 3)(4x - 5)\);

Phương pháp giải:

Cho nhị thức: \(f(x)=a x+b\) ta có:

+) \(f(x)\) cùng dấu với hệ số \(a\) khi \(x \in\left( { - \frac{b}{a};\, + \infty } \right).\)

+) \(f(x)\) trái dấu với hệ số \(a\) khi \(x \in \left( { + \infty ; \, - \frac{b}{a}} \right)\)

Cho đa thức bậc hai: \(f\left( x \right) = a{x^2} + bx + c\;\;\left( {a \ne 0} \right),\;\;\)\(\Delta  = {b^2} - 4ac.\)

+) Nếu \(\Delta < 0\) thì \(f(x)\) luôn cùng dấu với hệ số \(a,\) với mọi \(x \in R.\)

+) Nếu \(\Delta = 0\) thì \(f(x)\) luôn cùng dấu với hệ số \(a,\) trừ khi \(x=-\frac{b}{2a}.\)

+) Nếu \(\Delta > 0\) thì \(f(x)\) luôn cùng dấu với hệ số \(a\) khi \(x < x_1\) hoặc \(x > x_2,\) trái dấu với hệ số \(a\) khi \(x_1 < x < x_2\) trong đó \(x_1, \, \, x_2 \, \, (x_1 < x_2)\) là hai nghiệm của \(f(x).\)

Lời giải chi tiết:

\(f(x) =(3{x^2} - 10x + 3)(4x - 5)\) 

Ta có:

\(4x - 5 = 0 \Leftrightarrow x = \dfrac{5}{4}\)

\(3{x^2} - 10x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \dfrac{1}{3}\end{array} \right.\)

Tam thức bậc hai \(3{x^2} - 10x + 3\) có hệ số \(a=3>0\) nên mang dấu "+" khi \(x > 3\) hoặc \(x < \dfrac{1}{3}\) và mang dấu “-“ nếu \(\dfrac{1}{3} < x < 3\).

Xét dấu nhị thức \(4x - 5\) và \(3{x^2} - 10x + 3\) ta được bảng xét dấu:

Kết luận:

\(f(x) < 0\) với \(x \in \left( { - \infty ;{1 \over 3}} \right) \cup \left( {{5 \over 4};3} \right)\)

\(f(x) > 0\) với \(x \in \left( {{1 \over 3};{5 \over 4}} \right) \cup \left( {3; + \infty } \right)\)

LG b

\(f(x) = (3{x^2} - 4x)(2{x^2} - x - 1)\);

Lời giải chi tiết:

+ Tam thức 3x² – 4x có hai nghiệm x = 0 và x = 4/3, hệ số a = 3 > 0.

Do đó 3x² – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3.

+ Tam thức 2x² – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số a = 2 > 0

Do đó 2x² – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang dấu – khi –1/2 < x < 1.

Ta có bảng xét dấu:

Vậy \(f\left( x \right) > 0\;\;khi\;\;x \in \left( { - \infty ;\; - \frac{1}{2}} \right)\)\( \cup \left( {0;\;1} \right) \cup \left( {\frac{4}{3}; + \infty } \right).\)

\(f\left( x \right) < 0\;\;khi\;\;x \in \left( { - \frac{1}{2};\;0} \right) \cup \left( {1;\;\frac{4}{3}} \right).\)

LG c

\(f(x) =\)\( (4{x^2} - 1)( - 8{x^2} + x - 3)(2x + 9)\);

Lời giải chi tiết:

+ Tam thức 4x² – 1 có hai nghiệm x = –1/2 và x = 1/2, hệ số a = 4 > 0

Do đó 4x² – 1 mang dấu + nếu x < –1/2 hoặc x > 1/2 và mang dấu – nếu –1/2 < x < 1/2

+ Tam thức –8x² + x – 3 có Δ = –95 < 0, hệ số a = –8 < 0 nên luôn mang dấu –.

+ Nhị thức 2x + 9 có nghiệm x = –9/2.

Ta có bảng xét dấu:

Vậy \(f\left( x \right) > 0\;\;khi\;\;x \in \left( { - \infty ; - \frac{9}{2}} \right) \)\(\cup \left( { - \frac{1}{2};\;\frac{1}{2}} \right).\)

\(f\left( x \right) < 0\;\;khi\;\;x \in \left( { - \frac{9}{2}; - \frac{1}{2}} \right)\)\( \cup \left( {\frac{1}{2}; + \infty } \right).\)

LG d

\(f(x) = \dfrac{(3x^{2}-x)(3-x^{2})}{4x^{2}+x-3}.\)

Lời giải chi tiết:

+ Tam thức 3x² – x có hai nghiệm x = 0 và x = 1/3, hệ số a = 3 > 0.

Do đó 3x² – x mang dấu + khi x < 0 hoặc x > 1/3 và mang dấu – khi 0 < x < 1/3.

+ Tam thức 3 – x² có hai nghiệm x = √3 và x = –√3, hệ số a = –1 < 0

Do đó 3 – x² mang dấu – khi x < –√3 hoặc x > √3 và mang dấu + khi –√3 < x < √3.

+ Tam thức 4x² + x – 3 có hai nghiệm x = –1 và x = 3/4, hệ số a = 4 > 0.

Do đó 4x² + x – 3 mang dấu + khi x < –1 hoặc x > 3/4 và mang dấu – khi –1 < x < 3/4.

Ta có bảng xét dấu:

Vậy \(f\left( x \right) > 0\) khi \(x \in \left( { - \sqrt 3 ;\; - 1} \right) \cup \left( {0;\frac{1}{3}} \right) \cup \left( {\frac{3}{4};\;\sqrt 3 } \right).\)

\(f\left( x \right) < 0\) khi \(x \in \left( { - \infty ;\; - \sqrt 3 } \right) \cup \left( { - 1;0} \right) \cup \left( {\frac{1}{3};\;\frac{3}{4}} \right)\)\( \cup \left( {\sqrt 3 ; + \infty } \right).\)

HocTot.Nam.Name.Vn