Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao

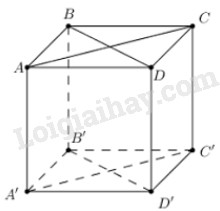
Bài 16

Hình hộp đứng ABCD.A’B’C’D’ có đáy là một hình thoi với diện tích S₁. Hai mặt chéo ACC’A’ và BDD’B’ có diện tích lần lượt bằng S₂ và S₃. Khi đó thể tích của hình hộp là

$\eqalign{  & (A)\;\sqrt {{{{S_1}{S_2}{S_3}} \over 2}} ;  \cr  & (B)\;{{\sqrt 2 } \over 3}\sqrt {{S_1}{S_2}{S_3}} ;  \cr  & (C)\;{{\sqrt 3 } \over 3}\sqrt {{S_1}{S_2}{S_3}} ;  \cr  & (D)\;{{{S_1}} \over 2}\sqrt {{S_2}{S_3}} . \cr}$

Lời giải chi tiết:

Chọn (A).

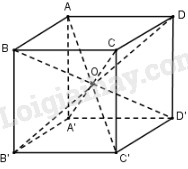
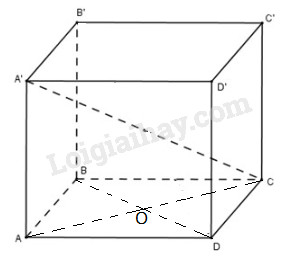
Các tứ giác ACC’A’ và BDD’B’ đều là hình chữ nhật nên:

$\begin{array}{l}{S_2} = AC.AA = AC.h\\{S_3} = BD.BB' = BD.h\\ \Rightarrow {S_2}{S_3} = AC.BD.{h^2} = 2{S_1}{h^2}\\ \Rightarrow h = \sqrt {\frac{{{S_2}{S_3}}}{{2{S_1}}}} \\ \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_1}h\\ = {S_1}.\sqrt {\frac{{{S_2}{S_3}}}{{2{S_1}}}}  = \sqrt {\frac{{{S_1}{S_2}{S_3}}}{2}} \end{array}$

Quảng cáo

Bài 17

Cho hình lập phương ABCD.A’B’C’D’  cạnh a, tâm O. Khi đó thể tích khối tứ diện AA’B’O là

$\eqalign{  & (A)\;{{{a^3}} \over 8};  \cr  & (B)\;{{{a^3}} \over {12}};  \cr  & (C)\;{{{a^3}} \over 9};  \cr  & (D)\;{{{a^3}\sqrt 2 } \over 3}. \cr}$

Lời giải chi tiết:

Chọn (B).

$\begin{array}{l} {V_{AA'B'O}} = {V_{O.AA'B}} = \frac{1}{2}{V_{O.ABB'A'}}\\ = \frac{1}{2}.\frac{1}{6}{V_{ABCD.A'B'C'D'}}\\ = \frac{1}{{12}}{a^3} \end{array}$

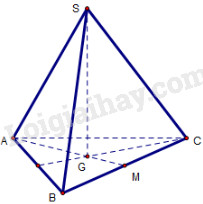
Bài 18

Cho biết thể tích của một hình hộp chữ nhật là V, đáy là hình vuông cạnh a. Khi đó diện tích toàn phần của hình hộp bằng

$\eqalign{  & (A)\;2\left( {{V \over a} + {a^2}} \right);  \cr  & (B)\;4{V \over a} + 2{a^2};\cr  & (C)\;2\left( {{V \over {{a^2}}} + a} \right);    \cr  & (D)\;4\left( {{V \over {{a^2}}} + a} \right). \cr}$

Lời giải chi tiết:

Chọn (B).

Diện tích đáy ${S_d} = {a^2}$

Chiều cao $h = \frac{V}{{{S_d}}} = \frac{V}{{{a^2}}}$

Diện tích xung quanh hình hộp: ${S_{xq}} = 4ah = 4a.\frac{V}{{{a^2}}} = \frac{{4V}}{a}$

Diện tích toàn phần: ${S_{tp}} = {S_{xq}} + 2{S_d} = \frac{{4V}}{a} + 2{a^2}$.

Bài 19

Cho một hình chóp tam giác có đường cao bằng 100cm và các cạnh đáy bằng 20cm, 21cm,29cm. Thể tích của hình chóp đó bằng

$\eqalign{  & (A)\;6000c{m^3};  \cr  & (B)\;6213c{m^3};  \cr  & (C)\;7000c{m^3};  \cr  & (D)\;7000\sqrt 2 c{m^3}  \cr}$

Lời giải chi tiết:

Chọn (C).

Nửa chu vi đáy: $p = \frac{{20 + 21 + 29}}{2} = 35$

Diện tích đáy:

$\begin{array}{l}{S_d} = \sqrt {35\left( {35 - 20} \right)\left( {35 - 21} \right)\left( {35 - 29} \right)} \\ = 210\\ \Rightarrow V = \frac{1}{3}Sh = \frac{1}{3}.210.100 = 7000\left( {c{m^3}} \right)\end{array}$

Bài 20

Cho hình chóp tam giác S.ABC với $SA \bot SB,SB \bot SC,SC \bot SA,$

$SA = a,SB = b,SC = c.$ Thể tích của hình chóp bằng

$\eqalign{  & (A)\;{1 \over 3}abc;  \cr  & (B)\;{1 \over 6}abc;  \cr  & (C)\;{1 \over 9}abc;  \cr  & (D)\;{2 \over 3}abc. \cr}$

Lời giải chi tiết:

Chọn (B).

Ta có:

$\left\{ \begin{array}{l}SA \bot SB\\SA \bot SC\end{array} \right. \Rightarrow SA \bot \left( {SBC} \right)$

$\begin{array}{l} \Rightarrow {V_{S.ABC}} = \frac{1}{3}SA.{S_{SBC}}\\ = \frac{1}{3}SA.\frac{1}{2}SB.SC = \frac{1}{6}abc\end{array}$

Bài 21

Một hình chóp tam giác đều có cạnh bên bằng b và chiều cao h. Khi đó, thể tích của hình chóp bằng

$\eqalign{  & (A){{\sqrt 3 } \over 4}\left( {{b^2} - {h^2}} \right)h;  \cr  & (B){{\sqrt 3 } \over {12}}\left( {{b^2} - {h^2}} \right)h;  \cr  & (C){{\sqrt 3 } \over 4}\left( {{b^2} - {h^2}} \right)b;  \cr  & (D){{\sqrt 3 } \over 8}\left( {{b^2} - {h^2}} \right)h; \cr}$

Lời giải chi tiết:

Chọn (A).

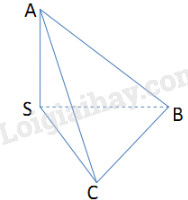
Xét hình chóp tam giác đều $S.ABC$ có chiều cao $SG = h$, cạnh bên $SA = b$.

Gọi M là trung điểm của BC ta có:

$AG = \sqrt {S{A^2} - S{G^2}}  = \sqrt {{b^2} - {h^2}}$

Tam giác ABC đều có $R = AG = \sqrt {{b^2} - {h^2}}$ nên:

$AB = 2R\sin C = 2\sqrt {{b^2} - {h^2}} \sin {60^0}$ $= \sqrt 3 .\sqrt {{b^2} - {h^2}}$

$\Rightarrow {S_{ABC}} = \frac{{A{B^2}\sqrt 3 }}{4}$

$= \frac{{3\left( {{b^2} - {h^2}} \right)\sqrt 3 }}{4}$

$\begin{array}{l} \Rightarrow {V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SG\\ = \frac{1}{3}.\frac{{3\left( {{b^2} - {h^2}} \right)\sqrt 3 }}{4}.h\\ = \frac{{\sqrt 3 \left( {{b^2} - {h^2}} \right)}}{4}.h\end{array}$

Bài 22

Cho hình chóp tam giác S.ABC có $SA \bot SB,SB \bot SC,SC \bot SA$ và AB=13cm, BC=15cm, CA=$\sqrt {106}$cm. Thể tích của hình chóp bằng

$\eqalign{  & (A)\;90c{m^3};  \cr  & (B)\;80c{m^3};  \cr  & (C)\;92c{m^3};  \cr  & (D)\;80\sqrt 2 c{m^3}. \cr}$

Lời giải chi tiết:

Chọn (A).

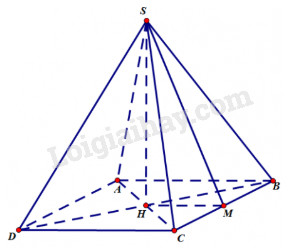
Các tam giác SAB, SBC, SCA đều vuông tại S nên ta có:

$\begin{array}{l}\left\{ \begin{array}{l}S{A^2} + S{B^2} = A{B^2}\\S{B^2} + S{C^2} = B{C^2}\\S{C^2} + S{A^2} = A{C^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}S{A^2} + S{B^2} = 169\\S{B^2} + S{C^2} = 225\\S{C^2} + S{A^2} = 106\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}S{A^2} = 25\\S{B^2} = 144\\S{C^2} = 81\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}SA = 5\\SB = 12\\SC = 9\end{array} \right.\\ \Rightarrow {V_{S.ABC}} = \frac{1}{6}SA.SB.SC\\ = \frac{1}{6}.5.12.9 = 90\end{array}$

Bài 23

Cho hình chóp tứ giác đều có cạnh đáy bằng a và mặt bên tạo với mặt đáy một góc 45⁰. Thể tích của hình chóp đó bằng

$\eqalign{  & (A){{{a^3}} \over 3};  \cr  & (B){{{a^3}} \over 6};  \cr  & (C){{2{a^3}} \over 3};  \cr  & (D){{{a^3}} \over 9}. \cr}$

Lời giải chi tiết:

Chọn (B).

Gọi H là tâm đáy, M là trung điểm của BC.

Khi đó $\widehat {SMH} = {45^0}$ nên tam giác SHM vuông cân tại H.

Ta có: $HM = \frac{1}{2}AB = \frac{a}{2}$

$\begin{array}{l} \Rightarrow SH = HM = \frac{a}{2}\\ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SH\\ = \frac{1}{3}{a^2}.\frac{a}{2} = \frac{{{a^3}}}{6}\end{array}$

Bài 24

Cho một hình chóp tứ giác đều có cạnh đáy bằng a và diện tích xung quanh gấp đôi diện tích đáy. Khi đó, thể tích của hình chóp bằng

$\eqalign{  & (A){{{a^3}\sqrt 3 } \over 6};  \cr  & (B){{{a^3}\sqrt 3 } \over 3};  \cr  & (C){{{a^3}\sqrt 3 } \over 2};  \cr  & (D){{{a^3}\sqrt 3 } \over {12}}. \cr}$

Lời giải chi tiết:

Chọn (A).

Diện tích đáy ${S_{ABCD}} = {a^2}$

Diện tích xung quanh ${S_{xq}} = 2{S_{ABCD}} = 2{a^2}$

$\begin{array}{l} \Rightarrow {S_{SBC}} = \frac{1}{4}{S_{xq}} = \frac{1}{4}.2{a^2} = \frac{{{a^2}}}{2}\\ \Rightarrow SM = \frac{{2{S_{SBC}}}}{{BC}} = \frac{{2.\frac{{{a^2}}}{2}}}{{{a^2}}} = a\\ \Rightarrow SH = \sqrt {S{M^2} - H{M^2}} \\ = \sqrt {{a^2} - \frac{{{a^2}}}{4}}  = \frac{{a\sqrt 3 }}{2}\\ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SH\\ = \frac{1}{3}.{a^2}.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{6}\end{array}$

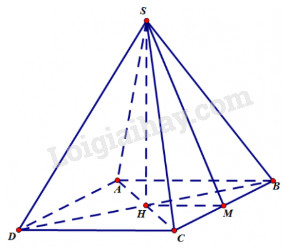
Bài 25

Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên tạo với mặt phẳng đáy một góc 60⁰. Thể tích của hình chóp đó bằng

$\eqalign{  & (A){{{a^3}\sqrt 6 } \over 2};  \cr  & (B){{{a^3}\sqrt 6 } \over 3};  \cr  & (C){{{a^3}\sqrt 3 } \over 2};  \cr  & (D){{{a^3}\sqrt 6 } \over 6}.  \cr}$

Lời giải chi tiết:

Chọn (D).

Gọi O là tâm đáy, khi đó $\widehat {SAO} = {60^0}$.

ABCD là hình vuông cạnh a nên $AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}$

Tam giác SAO vuông tại O nên $SO = AO\tan \widehat {SAO}$ $= \frac{{a\sqrt 2 }}{2}.\tan {60^0} = \frac{{a\sqrt 6 }}{2}$

Thể tích khối chóp ${V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SO$ $= \frac{1}{3}{a^2}.\frac{{a\sqrt 6 }}{2} = \frac{{{a^3}\sqrt 6 }}{6}$

Bài 26

Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng b. Khi đó thể tích của hình chóp bằng

$\eqalign{  & (A){1 \over 3}{a^2}\sqrt {{b^2} - 2{a^2}} ;  \cr  & (B){1 \over 6}{a^2}\sqrt {{b^2} - 2{a^2}} ;  \cr  & (C){1 \over 6}{a^2}\sqrt {4{b^2} - 2{a^2}} ;  \cr  & (D){2 \over 3}{a^2}\sqrt {2{b^2} - {a^2}} . \cr}$

Lời giải chi tiết:

Chọn (C ).

ABCD là hình vuông cạnh a nên $AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}$

Tam giác SAO vuông tại O nên $SO = \sqrt {S{A^2} - A{O^2}}$  $= \sqrt {{b^2} - \frac{{{a^2}}}{2}}  = \frac{1}{2}\sqrt {4{b^2} - 2{a^2}}$

Thể tích khối chóp: ${V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SO$ $= \frac{1}{3}{a^2}.\frac{1}{2}\sqrt {4{b^2} - 2{a^2}}$ $= \frac{1}{6}{a^2}\sqrt {4{b^2} - 2{a^2}}$

Bài 27

Một hình chóp tam giác đều có cạnh đáy bằng a và các mặt bên tạo với mặt phẳng đáy một góc 60⁰. Thể tích của hình chóp đó bằng

$\eqalign{  & (A){{{a^3}\sqrt 3 } \over {24}};  \cr  & (B){{{a^3}\sqrt 3 } \over 8};  \cr  & (C){{{a^3}\sqrt 3 } \over 4};  \cr  & (D){{{a^3}\sqrt 2 } \over 6}. \cr}$

Lời giải chi tiết:

Chọn (A).

Gọi H là tâm đáy, M là trung điểm của BC.

Khi đó $\widehat {SMH} = {60^0}$.

Tam giác ABC đều cạnh a nên $AM = \frac{{a\sqrt 3 }}{2}$

$MH = \frac{1}{3}AM = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}$

Tam giác SMH vuông có $\widehat {SMH} = {60^0}$ nên

$SH = MH\tan {60^0}$ $= \frac{{a\sqrt 3 }}{6}.\sqrt 3  = \frac{a}{2}$

Thể tích khối chóp ${V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SH$ $= \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.\frac{a}{2} = \frac{{{a^3}\sqrt 3 }}{{24}}$

Bài 28

Đường chéo của một hình hộp chữ nhật bằng d, góc giữa đường chéo và mặt đáy là $\alpha$, góc nhọn giữa hai đường chéo của đáy bằng $\beta$. Thể tích của hình hộp đó bằng

$\eqalign{  & (A)\;{1 \over 2}{d^3}{\cos ^2}\alpha \sin \alpha \sin \beta ;  \cr  & (B)\;{1 \over 3}{d^3}{\cos ^2}\alpha \sin \alpha \sin \beta ;  \cr  & (C)\;{d^3}{\sin ^2}\alpha \cos \alpha \sin \beta ;  \cr  & (D)\;{1 \over 2}{d^3}{\sin ^2}\alpha \cos \alpha \sin \beta . \cr}$

Lời giải chi tiết:

Chọn (A).

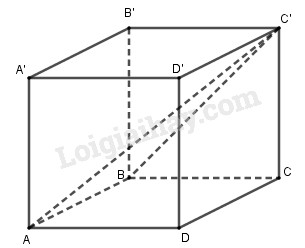
Gọi O là tâm đáy $ABCD$, giả sử $\widehat {AOB}$ nhọn thì $\widehat {AOB} = \beta$.

Ta có: $A'C = d,\widehat {A'CA} = \alpha$

Tam giác A’AC vuông tại A nên $A'A = A'C\sin \alpha  = d\sin \alpha$

$AC = A'C\cos \alpha  = d\cos \alpha$

$\Rightarrow AO = BO = CO = DO$ $= \frac{1}{2}AC = \frac{{d\cos \alpha }}{2}$

$\begin{array}{l}{S_{ABCD}} = 4{S_{AOB}}\\ = 4.\frac{1}{2}AO.BO.\sin \widehat {AOB}\\ = 2A{O^2}\sin \widehat {AOB}\\ = 2.{\left( {\frac{{d\cos \alpha }}{2}} \right)^2}\sin \beta \\ = \frac{{{d^2}{{\cos }^2}\alpha \sin \beta }}{2}\\ \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABCD}}.AA'\\ = \frac{{{d^2}{{\cos }^2}\alpha \sin \beta }}{2}.d\sin \alpha \\ = \frac{1}{2}{d^3}{\cos ^2}\alpha \sin \alpha \sin \beta \end{array}$

Bài 29

Cho lăng trụ tứ giác đều ABCD.A’B’C’D’  có cạnh đáy bằng a, đường chéo AC’ tạo với mặt bên (BCC’B’) một góc $\alpha \left( {0 < \alpha  < {{45}^0}} \right)$. Khi đó, thể tích của khối lăng trụ bằng

$\eqalign{  & (A)\;{a^3}\sqrt {{{\cot }^3}\alpha  + 1} ;  \cr  & (B)\;{a^3}\sqrt {{{\cot }^3}\alpha  - 1} ;  \cr  & (C)\;{a^3}\sqrt {\cos 2\alpha } ;  \cr  & (D)\;{a^3}\sqrt {{{\tan }^2}\alpha  - 1} . \cr}$

Lời giải chi tiết:

Chọn (B).

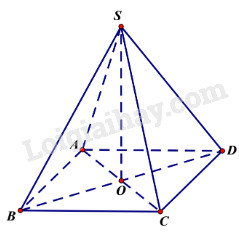
Ta có: $AB \bot \left( {BCC'B'} \right)$ nên $\left( {AC',\left( {BCC'B'} \right)} \right) = \widehat {AC'B} = \alpha$

Tam giác $ABC'$ vuông tại B nên $BC' = AB\cot \alpha  = a\cot \alpha$

Tam giác BCC’ vuông tại B nên $CC' = \sqrt {BC{'^2} - B{C^2}}$ $= \sqrt {{{\left( {a\cot \alpha } \right)}^2} - {a^2}}$$= a\sqrt {{{\cot }^2}\alpha  - 1}$

Thể tích: ${V_{ABCD.A'B'C'D'}} = {S_{ABCD}}.CC'$ $= {a^2}.a\sqrt {{{\cot }^2}\alpha  - 1}$ $= {a^3}\sqrt {{{\cot }^2}\alpha  - 1}$.

Bài 30

Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy và có độ dài bằng a. Thể tích khối tứ diện SBCD bằng

$\eqalign{  & (A)\;{{{a^3}} \over 3};  \cr  & (B)\;{{{a^3}} \over 4};  \cr  & (C)\;{{{a^3}} \over 6};  \cr  & (D)\;{{{a^3}} \over 8}. \cr}$

Lời giải chi tiết:

Chọn (C).

$\begin{array}{l} {V_{S.BCD}} = \frac{1}{3}{S_{BCD}}.SA\\ = \frac{1}{3}.\frac{1}{2}{S_{ABCD}}.SA\\ = \frac{1}{6}{a^2}.a = \frac{{{a^3}}}{6} \end{array}$

Bài 31

Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, còn cạnh bên SC tạo với mặt phẳng (SAB) một góc 30⁰. Thể tích của khối chóp đó bằng

$\eqalign{  & (A){{{a^3}\sqrt 3 } \over 3};  \cr  & (B){{{a^3}\sqrt 2 } \over 4};  \cr  & (C){{{a^3}\sqrt 2 } \over 2};  \cr  & (D){{{a^3}\sqrt 2 } \over 3}. \cr}$

Lời giải chi tiết:

Chọn (D).

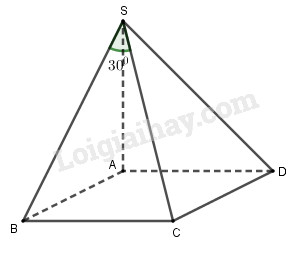
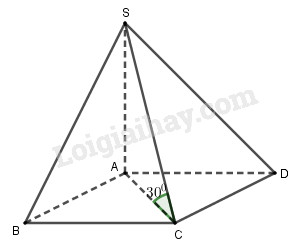
Ta có: $\left\{ \begin{array}{l}CB \bot AB\\CB \bot SA\end{array} \right. \Rightarrow CB \bot \left( {SAB} \right)$

Do đó góc $\left( {SC,\left( {SAB} \right)} \right) = \widehat {CSB} = {30^0}$.

Tam giác SBC vuông tại B nên $SB = \frac{{BC}}{{\tan {{30}^0}}} = \frac{a}{{\frac{{\sqrt 3 }}{3}}} = a\sqrt 3$

Tam giác SAB vuông tại A nên $SA = \sqrt {S{B^2} - A{B^2}}$ $= \sqrt {3{a^2} - {a^2}}  = a\sqrt 2$

Thể tích khối chóp ${V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SA$ $= \frac{1}{3}{a^2}.a\sqrt 2  = \frac{{{a^3}\sqrt 2 }}{3}$

Bài 32

Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a. Các mặt phẳng (SAB), (SAD) cùng vuông góc với mặt phẳng đáy , còn cạnh bên SC tạo với mặt phẳng đáy một góc 30⁰. Thể tích của hình chóp đã cho bằng

$\eqalign{  & (A){{{a^3}\sqrt 6 } \over 9};  \cr  & (B){{{a^3}\sqrt 6 } \over 3};  \cr  & (C){{{a^3}\sqrt 6 } \over 4};  \cr  & (D){{{a^3}\sqrt 3 } \over 9}. \cr}$

Lời giải chi tiết:

Chọn (A).

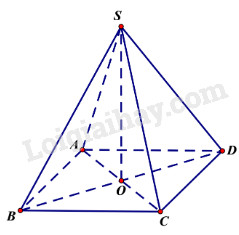
Ta có: $\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {SAD} \right) = SA\end{array} \right.$

$\Rightarrow SA \bot \left( {ABCD} \right)$

$\Rightarrow$ góc giữa $SC$ và $\left( {ABCD} \right)$ bằng $\widehat {SCA} = {30^0}$.

ABCD là hình vuông cạnh $a$ nên $AC = a\sqrt 2$

Tam giác SAC vuông tại A nên:

$SA = AC\tan \widehat {SCA}$ $= a\sqrt 2 .\tan {30^0} = \frac{{a\sqrt 6 }}{3}$

Thể tích khối chóp ${V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SA$ $= \frac{1}{3}{a^2}.\frac{{a\sqrt 6 }}{3} = \frac{{{a^3}\sqrt 6 }}{9}$

HocTot.Nam.Name.Vn