Bài 15 trang 63 SGK Toán 7 tập 2Dựa vào bất đẳng thức tam giác, Đề bài Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác. Trong các trường hợp còn lại, hãy thử dựng tam giác có độ dài ba cạnh như thế: a) 2cm,3cm,6cm.2cm,3cm,6cm. b) 2cm,4cm,6cm.2cm,4cm,6cm. c) 3cm,4cm,6cm.3cm,4cm,6cm. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Khi xét độ dài ba đoạn thẳng có thỏa mãn bất đẳng thức tam giác hay không ta chỉ cần so sánh độ dài lớn nhất với tổng hai độ dài còn lại hoặc so sánh độ dài nhỏ nhất với hiệu hai độ dài còn lại. + Định lí: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại + Hệ quả: Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại. Lời giải chi tiết a) Ta có 6−3=3>26−3=3>2, do đó ba độ dài 2cm,3cm,6cm2cm,3cm,6cm không là ba cạnh của tam giác. b) Vì 6=2+46=2+4 nên ba độ dài là 2cm,4cm,6cm2cm,4cm,6cm không là ba cạnh của một tam giác. c) Ta có: 4−3<6<4+34−3<6<4+3, do đó ba độ dài 3cm,4cm,6cm3cm,4cm,6cm là ba cạnh của một tam giác.
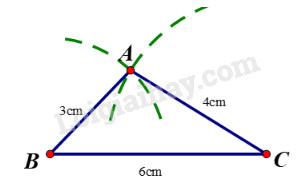
Cách dựng tam giác có ba độ dài 3cm, 4cm, 6cm - Vẽ BC = 6cm - Dựng đường tròn tâm B bán kính 3cm; đường tròn tâm C bán kính 4cm. Hai đường tròn cắt nhau tại A. - Nối AB, AC ta được tam giác cần dựng. HocTot.Nam.Name.Vn
|