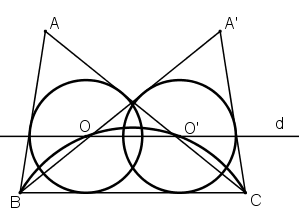
Bài 14 trang 135 SGK Toán 9 tập 2Dựng tam giác ABC, biết BC = 4cm, góc A = 60o, bán kính đường tròn nội tiếp tam giác bằng 1cm. Đề bài Dựng tam giác \(ABC\), biết \(BC = 4cm\), góc \(\widehat {A} = 60^0\), bán kính đường tròn nội tiếp tam giác bằng \(1cm\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Góc có đỉnh ở ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn. Lời giải chi tiết Phân tích: Giả sử dựng được ΔABC thỏa mãn điều kiện. Gọi O là tâm đường tròn nội tiếp tam giác. \(\widehat {BOC} = 180^\circ - \left( {\widehat {OBC} + \widehat {OCB}} \right) \\= 180^\circ - \dfrac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\) \( = 180^\circ - \dfrac{1}{2}\left( {180^\circ - \widehat A} \right) \\= 180^\circ - \dfrac{1}{2}\left( {180^\circ - 60^\circ } \right) = 120^\circ \) ⇒ O thuộc cung chứa góc 120º dựng trên đoạn BC. + Bán kính đường tròn nội tiếp ΔABC bằng 1 ⇒ O cách BC 1cm ⇒ O thuộc d // BC và cách BC 1cm. Vậy O là giao của cung chứa góc 120º dựng trên đoạn BC và đường thẳng d. Cách dựng: Dựng \(BC = 4cm\) và đường thẳng \((d)\) song song với \(BC\) và cách \(BC\) một khoảng là \(1cm.\) Tâm \(O\) của đường tròn nội tiếp \(∆ABC\) là giao điểm của đường thẳng \((d)\) với cung chứa góc \({120^0}\) dựng trên đoạn \(BC\) cố định. Qua \(B\) và \(C\) vẽ các tiếp tuyến với \((O;1cm)\), chúng cắt nhau tại \(A.\) Tam giác \(ABC\) là tam giác phải dựng. Chứng minh: + Theo cách dựng có BC = 4cm . + O thuộc cung 120º dựng trên đoạn BC \( \Rightarrow \widehat {BOC} = {120^0}\) + A là giao của 2 tiếp tuyến ⇒ (O; 1cm) tiếp xúc với AB và AC Mà khoảng cách từ O đến BC = 1cm ⇒ (O; 1cm) cũng tiếp xúc với BC ⇒ (O; 1cm) là đường tròn nội tiếp ΔABC \( \Rightarrow \widehat {BAC} = \dfrac{1}{2}\widehat {BOC} \)\(= \dfrac{{{{120}^0}}}{2} = {60^0}\) (số đo góc nội tiếp bằng nửa số đo góc ở tâm) Vậy ΔABC có BC = 4cm, \( \widehat {BAC} = {60^0}\) đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu. Biện luận: Vì d cắt m tại hai điểm nên bài toán có hai nghiệm hình \(ΔABC\) và \(ΔA’BC\) như hình vẽ. HocTot.Nam.Name.Vn
|