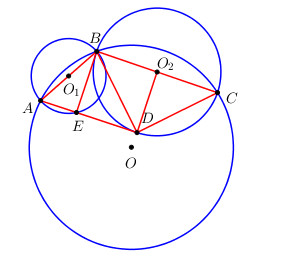
Bài 12 trang 94 Tài liệu dạy – học Toán 9 tập 2

Đề bài

Gọi A, B, C là ba điểm theo thứ tự trên một đường thẳng. Vẽ hai đường tròn đường kính AB và BC. Từ A vẽ các đường thẳng tiếp xúc với đường tròn đường kính BC tại D và cắt đường tròn đường kính AB tại E. Chứng minh BD là phân giác góc $\widehat {EBC}$.

Lời giải chi tiết

 

Gọi O₁ và O₂ lần lượt là tâm đường tròn đường kính AB và đường tròn đường kính BC.

Xét đường tròn đường kính AB có $\widehat {AEB} = {90^0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow AE \bot BE$

Vì AD là tiếp tuyến của đường tròn đường kính BC tại D nên ${O_2}D \bot AD$ hay ${O_2}D \bot AE$

Từ đó suy ra ${O_2}D//BE$ (cùng vuông góc với AE) $\Rightarrow \widehat {EBD} = \widehat {{O_2}DB}$ (1) (so le trong)

Mà ${O_2}B = {O_2}D \Rightarrow \Delta {O_2}BD$ cân tại O₂$\Rightarrow \widehat {{O_2}DB} = \widehat {{O_2}BD}$ (2).

Từ (1) và (2) $\Rightarrow \widehat {EBD} = \widehat {{O_2}BD} \Rightarrow BD$ là phân giác của góc $\widehat {EBC}$ (đpcm).

 HocTot.Nam.Name.Vn