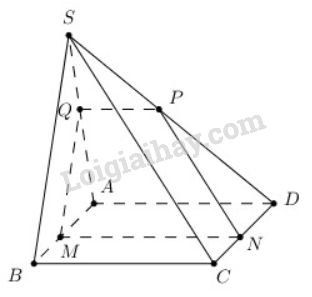
Bài 11 trang 80 SGK Hình học 11Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Đề bài Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng (α) song song với (SBC) Thiết diện tạo bởi (α) và hình chóp S.ABCD là hình gì? (A) Tam giác (B) Hình bình hành (C) Hình thang (D) Hình vuông Video hướng dẫn giải Phương pháp giải - Xem chi tiết Xác định thiết diện, sử dụng tính chất: Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau. Quảng cáo  Lời giải chi tiết
Trong (ABCD) qua M kẻ MN//BC Trong (SAB) qua M kẻ MQ//SB Trong (SCD) qua N kẻ NP//SC. Từ đó ta có thiết diện của hình chóp khi cắt bởi mặt phẳng (α) là tứ giác MNPQ. Ta có {(MNPQ)∩(SAD)=PQ(MNPQ)∩(ABCD)=MN(ABCD)∩(SAD)=AD ⇒PQ//MN//AD Vậy MNPQ là hình thang. Chọn đáp án C. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|
