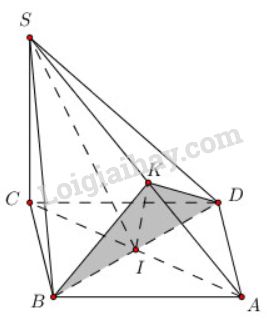
Bài 11 trang 114 SGK Hình học 11

Đề bài

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một hình thoi tâm \(I\) cạnh \(a\) và có góc \(A\) bằng \(60^{0},\) cạnh \(SC=\dfrac{a\sqrt{6}}{2}\) và \(SC\) vuông góc với mặt phẳng \((ABCD)\).

a) Chứng minh mặt phẳng \((SBD)\) vuông góc với mặt phẳng \((SAC)\). 

b) Trong tam giác \(SCA\) kẻ \(IK\) vuông góc với \(SA\) tại \(K\). Hãy tính độ dài \(IK\)

c) Chứng minh \(\widehat{BKD}=90^{0}\) và từ đó suy ra mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((SAD)\).

Lời giải chi tiết

a) \(SC \bot \left( {ABCD} \right) \Rightarrow SC \bot BD\,\,\,\,\,\,\,\,\,\left( 1 \right)\)

\(ABCD\) là hình thoi nên \(AC\bot BD\,\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra \(BD ⊥ (SAC)\).

Mà \(BD\subset (SBD)\Rightarrow (SBD) ⊥ (SAC)\).

b) Xét tam giác \(ABD\) có \(AB=AD\) và góc \(A=60^0\) nên là tam giác đều.

Do đó \(AI=\dfrac {a\sqrt 3 }  2\Rightarrow AC = 2AI = a\sqrt 3 \)

\(SC \bot \left( {ABCD} \right) \Rightarrow SC \bot CA\) nên tam giác \(SAC\) vuông tại \(C\).

Xét tam giác vuông \(SAC\) có: \(SA=\sqrt {A{C^2} + S{C^2}}  = \sqrt {3{a^2} + \dfrac {6{a^2}}  4} \) \(=\dfrac{3a}{\sqrt{2}}.\) 

Xét \(\Delta SCA\) và \(\Delta IKA\) có:

\(\left\{ \begin{array}{l}
A\, \text {chung}\\
\widehat {SCA} = \widehat {IKA} = {90^0}
\end{array} \right.\)

\( \Rightarrow \) \(\Delta SCA \backsim \Delta IKA\,\,\left( {g.g} \right)\)

\(\Rightarrow \dfrac{IK}{SC}=\dfrac{AI}{AS}\) \(\Rightarrow IK=\dfrac{AI.SC}{AS}=\dfrac{a}{2}.\)

c) Dễ thấy \(\Delta ABD\) đều nên \(BD = a \) \(\Rightarrow IK = \dfrac{1}{2}BD\) nên \(\Delta BKD\) vuông tại \(K\).

Vậy \(\widehat{BKD}=90^{0}.\)

Ta có: \(BD \bot \left( {SAC} \right)\,\,\left( {cmt} \right) \Rightarrow BD \bot SA\)

\(\left\{ \begin{array}{l}BD \bot SA\\IK \bot SA\end{array} \right. \Rightarrow SA \bot \left( {BKD} \right) \Rightarrow \left\{ \begin{array}{l}SA \bot BK\\SA \bot DK\end{array} \right.\)

Ta có: 

\(\begin{array}{l}
\left\{ \begin{array}{l}
\left( {SAB} \right) \cap \left( {SAD} \right) = SA\\
\left( {SAB} \right) \supset BK \bot SA\\
\left( {SAD} \right) \supset DK \bot SA
\end{array} \right.\\
\end{array}\)

Suy ra góc giữa hai mặt phẳng \((SAB)\) và \((SAD)\) bằng góc giữa hai đường thẳng \(BK\) và \(DK\) là góc \(\widehat{BKD}=90^{0}.\) (đpcm)

HocTot.Nam.Name.Vn