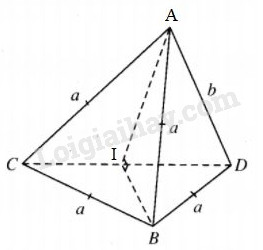
Bài 1 trang 54 SBT Hình học 12 Nâng cao

LG a

Chứng minh rằng tam giác ACD vuông.

Lời giải chi tiết:

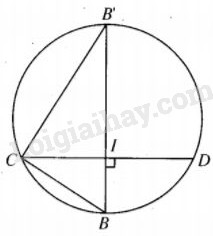
Gọi $I$ là trung điểm của CD, do BC = BD = a nên $BI \bot CD.$

Mặt khác $mp\left( {BCD} \right) \bot mp\left( {ACD} \right)$ nên $BI \bot mp(ACD).$

Xét các tam giác vuông AIB và DIB có cạnh góc vuông BI chung, BA = BD, từ đó AI = ID.

Vậy ACD là tam giác vuông tại A.

LG b

Tính diện tích mặt cầu ngoại tiếp tứ diện ABCD.

Lời giải chi tiết:

Từ chứng minh trên, ta thấy tâm của mặt cầu ngoại tiếp tứ diện ABCD thuộc BI, do đó, bán kính mặt cầu phải tìm chính là bán kính R của đường tròn ngoại tiếp tam giác BCD.

Dễ thấy CB²=BI.BB’=2R.BI, tức là $R = {{{a^2}} \over {2BI}}.$

Mặt khác

$\eqalign{  & B{I^2} = B{C^2} - {{C{D^2}} \over 4} = {a^2} - {{{a^2} + {b^2}} \over 4} = {{3{a^2} - {b^2}} \over 4}  \cr  &  \Rightarrow BI = {1 \over 2}\sqrt {3{a^2} - {b^2}} ,0 < b < a\sqrt 3 . \cr}$

Như vậy $R = {{{a^2}} \over {\sqrt {3{a^2} - {b^2}} }}$

Do đó diện tích mặt cầu phải tìm bằng ${{4\pi {a^4}} \over {3{a^2} - {b^2}}}$ với $0 < b < a\sqrt 3$.

HocTot.Nam.Name.Vn