Lý thuyết tổng ba góc của một tam giác

I. Các kiến thức cần nhớ 

1. Tổng ba góc của một tam giác

Định lý: Tổng ba góc của một tam giác bằng ${180^0}$.

Ví dụ: Với $\Delta ABC$ ta có $\widehat A + \widehat B + \widehat C = {180^0}$

2. Áp dụng vào tam giác vuông

Định nghĩa: Tam giác vuông là tam giác có một góc vuông.

Tính chất: Trong tam giác vuông, hai góc nhọn phụ nhau

Ví dụ: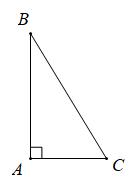 

$\left\{ \begin{array}{l}\Delta ABC\\\widehat A = {90^0}\end{array} \right. \Rightarrow \widehat B + \widehat C = {90^0}$

3. Góc ngoài của tam giác

+ Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc của tam giác.

+ Tính chất:

Mỗi góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.

Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó.

Ví dụ: Cho hình vẽ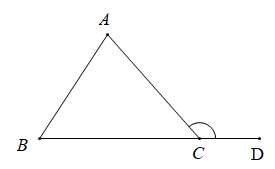

Ta có: : $\widehat {ACD} = \widehat A + \widehat B$, $\widehat {ACD} > \widehat A,\widehat {ACD} > \widehat B.$

II. Các dạng toán thường gặp

Dạng 1: Tính số đo góc của một tam giác

Phương pháp:

Lập các đẳng thức thể hiện:

+ Tổng ba góc của một tam giác bằng $180^\circ$

+ Trong tam giác vuông, hai góc nhọn phụ nhau

+ Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó

Từ đó tính số đo góc cần tìm.

Dạng 2: Nhận biết tam giác vuông

Phương pháp:

Đề nhận biết tam giác vuông ta chỉ ra tam giác đó có một góc bằng $90^\circ$. Trong tam giác vuông chú ý rằng hai góc nhọn phụ nhau.

Dạng 3: So sánh các góc dựa vào tính chất góc ngoài của tam giác

Phương pháp:

Dùng tính chất: “Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó”.