Lí thuyết từ vuông góc đến song song1. Quan hệ giữa tính vuông góc và tính song song của ba đường thẳng Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn I. Các kiến thức cần nhớ 1. Quan hệ giữa tính vuông góc và tính song song của ba đường thẳng  Nếu hai đường thẳng (phân biệt) cùng vuông góc với một đường thẳng thứ ba thì song song với nhau. \(\left. \begin{array}{l}a \bot c\\b \bot c\end{array} \right\} \Rightarrow a//b\) 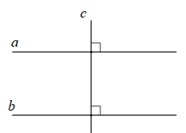  Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia. \(\left. \begin{array}{l}a//b\\c \bot a\end{array} \right\} \Rightarrow c \bot b\) 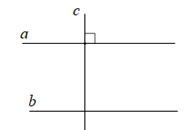 2. Ba đường thẳng song song  Hai đường thẳng (phân biệt) cùng song song với một đường thẳng thứ ba thì chúng song song với nhau. \(\left. \begin{array}{l}a//c\\b//c\end{array} \right\} \Rightarrow a//b\) II. Các dạng toán thường gặp Dạng 1: Nhận biết hai đường thẳng song song, vuông góc Phương pháp: Xét tính vuông góc và tính song song của hai đường thẳng với đường thẳng thứ ba: + Nếu hai đường thẳng (phân biệt) cùng vuông góc với một đường thẳng thứ ba thì song song với nhau. + Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cùng vuông góc với đường thẳng kia. + Hai đường thẳng (phân biệt) cùng song song với một đường thẳng thứ ba thì chúng song song với nhau. Dạng 2: Tính số đo góc Phương pháp: Bước 1: Vẽ thêm đường thẳng (nếu cần thiết) Bước 2: Sử dụng tính chất của hai đường thẳng song song, hai góc kề bù… Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì: + Hai góc so le trong còn lại bằng nhau + Hai góc đồng vị bằng nhau + Hai góc trong cùng phía bù nhau
|













