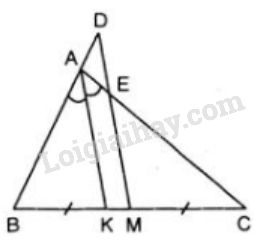
Bài 5 trang 156 Vở bài tập toán 8 tập 2Giải bài 5 trang 156 VBT toán 8 tập 2. Cho tam giác ABC; AB < AC). Tia phân giác của góc A cắt BC ở K. Qua trung điểm M của BC kẻ một tia song song với KA... Đề bài Cho tam giác \(ABC\; (AB < AC)\). Tia phân giác của góc \(A\) cắt \(BC\) ở \(K\). Qua trung điểm \(M\) của \(BC\) kẻ một tia song song với \(KA\) cắt đường thẳng \(AB\) ở \(D\), cắt \(AC\) ở \(E\). Chứng minh \(BD = CE\). Phương pháp giải - Xem chi tiết Áp dụng: Tính chất đường phân giác, tính chất hai tam giác đồng dạng. Lời giải chi tiết (h.116)
\(AK\) là đường phân giác của góc \(A\) (h.116) nên \(\dfrac{{BK}}{{BA}} = \dfrac{{CK}}{{CA}}\) (1) Vì \(MD//KA\) nên theo định lý Ta-lét ta có: \(\dfrac{{BK}}{{BA}} = \dfrac{{BM}}{{BD}},\dfrac{{CK}}{{CA}} = \dfrac{{CM}}{{CE}}\) (2) Từ (1) và (2) suy ra: \(\dfrac{{BM}}{{BD}} = \dfrac{{CM}}{{CE}}\) Do \(BM = CM\) nên \(BD = CE\). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
