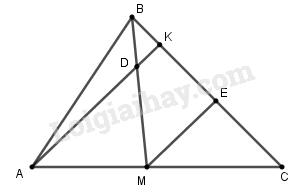
Bài 4 trang 156 Vở bài tập toán 8 tập 2Giải bài 4 trang 156 VBT toán 8 tập 2. Cho tam giác ABC và đường trung tuyến BM. Trên đoạn thẳng BM lấy điểm D sao cho . Tia AD cắt BC ở K. Tìm tỉ số diện tích của tam giác ABK và tam giác ABC. Đề bài Cho tam giác \(ABC\) và đường trung tuyến \(BM\). Trên đoạn thẳng \(BM\) lấy điểm \(D\) sao cho \(\dfrac{{B{\rm{D}}}}{{DM}} = \dfrac{1}{2}\) . Tia \(AD\) cắt \(BC\) ở \(K\). Tìm tỉ số diện tích của tam giác \(ABK\) và tam giác \(ABC.\) Phương pháp giải - Xem chi tiết Áp dụng: - Định lí: trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ 3. - Công thức tính diện tích tam giác. Lời giải chi tiết (h.115)
Kẻ \(ME//AK\left( {E \in BC} \right)\) (h.115) Theo định lý Ta-lét, trong tam giác \(BME\), ta có: \(\dfrac{{BK}}{{KE}} = \dfrac{{BD}}{{DM}} = \dfrac{1}{2}\) Suy ra \(KE = 2BK.\) \(M\) là trung điểm của \(AC\) và \(ME//AK\) nên \(E\) là trung điểm của \(KC\). Ta có: \(EC = KE = 2BK\) Do đó \(BC = BK + KE + EC = 5BK,\) suy ra \(\dfrac{{BK}}{{BC}} = \dfrac{1}{5}\) Vậy \(\dfrac{{{S_{ABK}}}}{{{S_{ABC}}}} = \dfrac{{BK}}{{BC}} = \dfrac{1}{5}\) (Hai tam giác \(ABK\) và \(ABC\) có chung đường cao hạ từ \(A\)) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
