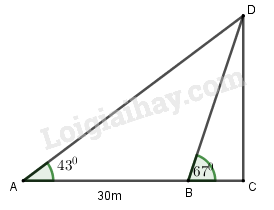
Bài 2.43 trang 103 SBT hình học 10Giải bài 2.43 trang 103 sách bài tập hình học 10. Giả sử chúng ta cần đo chiều cao CD của một cái tháp với C là chân tháp... Đề bài Giả sử chúng ta cần đo chiều cao CD của một cái tháp với C là chân tháp, D là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm A, B có khoảng cách AB = 30 m sao cho ba điểm A, B, C thẳng hàng người ta đo được các góc \(\widehat {CAD} = {43^0},\widehat {CBD} = {67^0}\). Hãy tính chiều cao CD của tháp.
Phương pháp giải - Xem chi tiết - Tính \(\widehat {ADB}\). Sử dụng định lý sin trong tam giác \(ABD\) tính \(BD\). - Tính \(CD\) dựa vào hệ thức lượng trong tam giác vuông. Lời giải chi tiết Ta có: \(\widehat {ADB} = {67^0} - {43^0} = {24^0}\) Theo định lí sin đối với tam giác ABD ta có: \(\dfrac{{BD}}{{\sin {{43}^0}}} = \dfrac{{AB}}{{\sin {{24}^0}}}\)\( \Rightarrow BD = \dfrac{{30.\sin {{43}^0}}}{{\sin {{24}^0}}} \approx 50,30(m)\) Trong tam giác vuông BCD ta có: \(\sin {67^0} = \dfrac{{CD}}{{BD}}\)\( \Rightarrow CD = BD.\sin {67^0} \approx 50,30.\sin {67^0}\) Hay \(CD \approx 46,30(m)\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
2k8 Tham gia ngay group chia sẻ, trao đổi tài liệu học tập miễn phí
|
