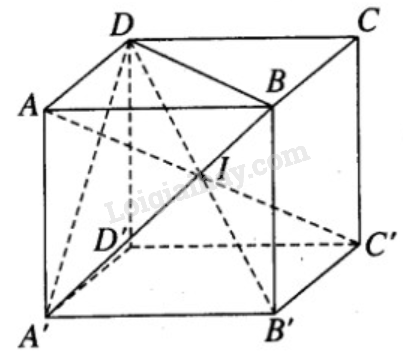
Bài 2.31 trang 63 SBT hình học 12

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ cạnh a.

a) Tính diện tích xung quanh của hình trụ có đường tròn hai đáy ngoại tiếp các hình vuông ABC.D và A’B’C’D’.

b) Tính diện tích mặt cầu đi qua tất cả các đỉnh  của hình lập phương.

c) Tính diện tích xung quanh của hình nón tròn xoay nhận đường thẳng  AC’ làm trục và sinh ra bởi cạnh AB.

Lời giải chi tiết

a) Hình trụ có chiều cao h = a và bán kính đáy \(\displaystyle r = {{a\sqrt 2 } \over 2}\)

Do đó ta có: \(\displaystyle {S_{xq}} = 2\pi rh = \pi {a^2}\sqrt 2 \).

b) Gọi I là tâm của hình lập phương.

Tất cả các đỉnh của hình lập phương đều có khoảng cách đến I bằng \(\displaystyle {{a\sqrt 3 } \over 2}\) nên chúng nằm trên mặt cầu tâm I bán kính \(\displaystyle r = {{a\sqrt 3 } \over 2}\).

Ta có diện tích mặt cầu đó là \(\displaystyle S = 4\pi {r^2} = 3\pi {a^2}\).

c) Đường tròn đáy của hình nón tròn xoay đỉnh A tạo nên bởi cạnh AB là đường tròn ngoại tiếp tam giác đều A’BD, tam giác này có cạnh bằng \(\displaystyle a\sqrt 2 \) và có đường cao bằng \(\displaystyle {{a\sqrt 6 } \over 2}\)

Do đó đường tròn đáy hình nón có bán kính \(\displaystyle r' = {{a\sqrt 6 } \over 3}\).

Vậy hình nón tròn xoay này có đường sinh \(\displaystyle l=a\) và có diện tích xung quanh là \(\displaystyle {S_{xq}} = \pi r'l = \pi .{{a\sqrt 6 } \over 3}.a = {{\pi {a^2}\sqrt 6 } \over 3}\).

HocTot.Nam.Name.Vn