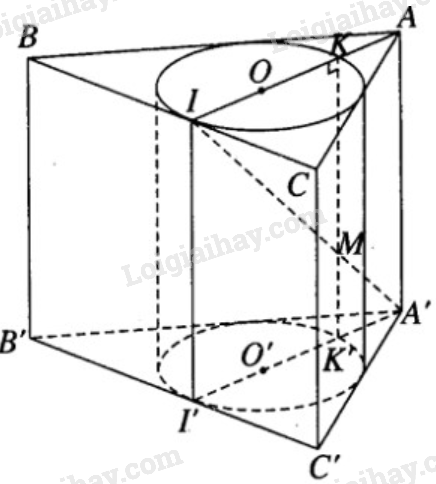
Bài 2.25 trang 62 SBT hình học 12

Đề bài

Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và có đường cao h. 

a) Một hình trụ có các đường tròn đáy tiếp xúc với các cạnh của tam giác đáy được gọi là hình trụ nội tiếp trong lăng trụ. Hãy tính diện tích xung quanh của hình trụ nội tiếp đó.

b) Gọi I là trung điểm của cạnh BC. Đường thẳng A’I cắt hình trụ nội tiếp nói trên theo một đoạn thẳng. Tính độ dài đoạn thẳng đó.

Lời giải chi tiết

a) Hình trụ nội tiếp trong lăng trụ tam giác đều có đường tròn đáy tiếp xúc tại trung điểm các cạnh của tam giác đáy. Gọi I là trung điểm của cạnh BC, r là bán kính đáy của hình trụ  nội tiếp trong lăng trụ, ta có: \(\displaystyle AI = {{a\sqrt 3 } \over 2}\).

Do đó, \(\displaystyle r = {{a\sqrt 3 } \over 6}\).

Ta có diện tích xung quanh của hình trụ nội tiếp lăng trụ là:

\(\displaystyle {S_{xq}} = 2\pi rl = 2\pi {{a\sqrt 3 } \over 6}.h \) \(\displaystyle = {{\sqrt 3 \pi ah} \over 3}\)

b) Ta có mặt phẳng (AA’I) là mặt phẳng qua trục hình trụ.

Mặt phẳng này cắt hình trụ theo thiết diện là hình chữ nhật IKK’I’.

Đoạn A’I cắt KK’ tại M nên cắt hình trụ theo đoạn IM.

Ta có: \(\displaystyle {{KM} \over {AA'}} = {{IK} \over {IA}} = {2 \over 3}\) \(\displaystyle \Rightarrow  KM = {2 \over 3}h\)

Xét tam giác vuông IKM ta có: \(\displaystyle I{M^2} = I{K^2} + K{M^2} \) \(\displaystyle = {{3{a^2}} \over 9} + {{4{h^2}} \over 9} = {{3{a^2} + 4{h^2}} \over 9}\)

Vậy \(\displaystyle IM = {{\sqrt {3{a^2} + 4{h^2}} } \over 3}\).

HocTot.Nam.Name.Vn