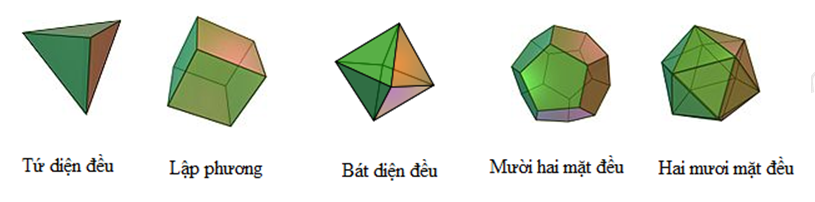50 bài tập trắc nghiệm khái niệm về khối đa diện mức độ nhận biết, thông hiểuLàm bàiCâu hỏi 1 : Trong các mệnh đề sau, mệnh đề nào sai?
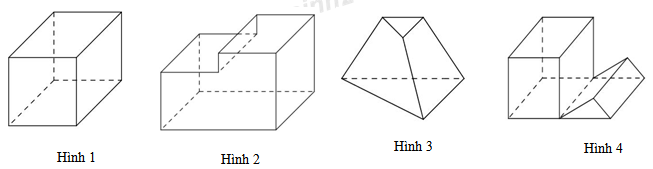
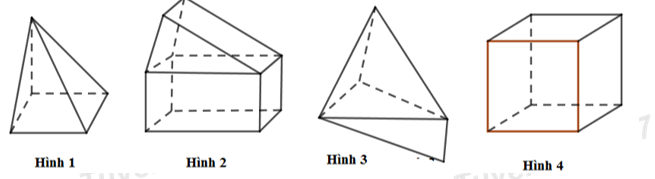
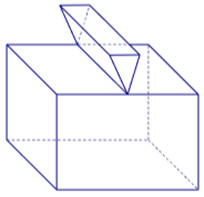
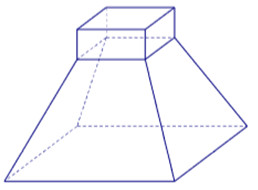
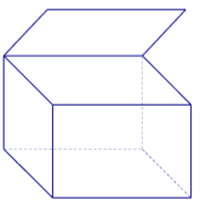
Đáp án: B Lời giải chi tiết: B Câu hỏi 2 : Vật thể nào trong các vật thể sau không phải là khối đa diện?
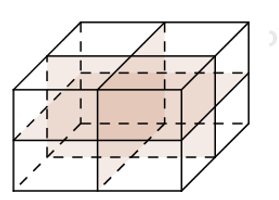
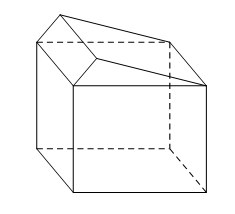
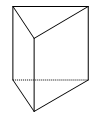
Đáp án: C Phương pháp giải: Lời giải chi tiết: Khái niệm khối đa diện đều: Khối đa diện là hình được tạo bởi hữu hạn các đa giác thỏa mãn hai điều kiện: - Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có đúng một đỉnh chung, hoặc chỉ có đúng 1 cạnh chung. - Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác. Quan sát 4 hình vẽ, hình C có cạnh trên cùng là cạnh chung của 4 đa giác, vậy hình này không phải là khối đa diện. Chọn C. Câu hỏi 3 : Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
Đáp án: A Lời giải chi tiết: Phương pháp + Cách giải: Hình lăng trụ tam giác đều có 1 mặt phẳng đối xứng đi qua trung điểm của các cạnh bên (song song với đáy) và 3 mặt phẳng đối xứng vuông góc với đáy (giao với 2 đáy theo các đường trung tuyến của tam giác đáy) Tất cả có 4 mặt phẳng Chọn A Câu hỏi 4 : Chọn khẳng định đúng trong các khẳng định sau.
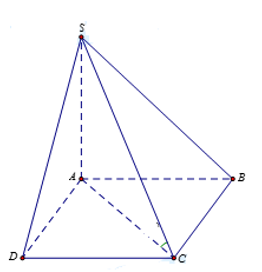
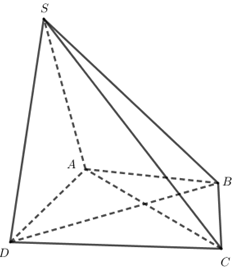
Đáp án: C Phương pháp giải: Vẽ hình và quan sát, chọn đáp án. Lời giải chi tiết: Quan sát hình vẽ bên ta thấy khối chóp \(S.ABCD\) được chia thành hai khối tứ diện \(S.ABC\) và \(S.ADC\) hay hai khối tứ diện \(C.SAB\) và \(C.SAD\).
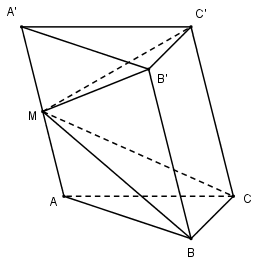
Câu hỏi 5 : Cho khối lăng trụ tam giác ABC.A'B'C', M là trung điểm của AA'.Cắt khối lăng trụ trên bằng hai mặt phẳng (MBC) và (MB'C')ta được:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Phương pháp: Phân chia khối đa diện. Cách giải Cắt khối lăng trụ bởi hai mặt phẳng (MBC) và (MB’C’) ta được ba khối chóp M.ABC ; M.A’B’C’ ; M.BCC’B’. Chọn B. Câu hỏi 6 : Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?
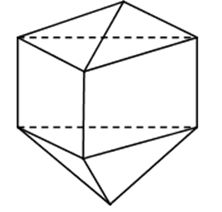
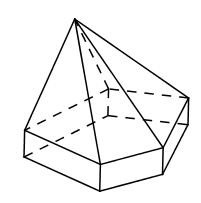
Đáp án: C Phương pháp giải: Lời giải chi tiết: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất 3 mặt. Chọn C. Câu hỏi 7 : Tìm số mặt của hình đa diện ở hình vẽ bên:
Đáp án: D Phương pháp giải: Phương pháp:
Quan sát hình vẽ và đếm. Lời giải chi tiết: Cách giải: Hình đa diện trên có 9 mặt. Chọn D. Câu hỏi 8 : Số cạnh của các hình đa diện luôn luôn:
Đáp án: A Phương pháp giải: Lấy tứ diện làm đại diện để xét. Lời giải chi tiết:
Dễ thấy số cạnh của hình đa diện luôn luôn lớn hơn hoặc bằng 6. Đáp án A Câu hỏi 9 : Mỗi hình sau gồm một số hữu hạn đa giác phẳng, tìm hình không là hình đa diện.
Đáp án: B Phương pháp giải: Khái niệm: Hình đa diện gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện: a) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung. b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác. Hình đa diện chia không gian thành hai phần (phần bên trong và phần bên ngoài). Hình đa diện cùng với phần bên trong của nó gọi là khối đa diện.
Lời giải chi tiết: Theo khái niệm hình đa diện ta chỉ thấy hình 4 không là hình đa diện. Câu hỏi 10 : Hình đa diện sau có bao nhiêu mặt ?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 11 : Hình đa diện trong hình bên có bao nhiêu mặt và bao nhiêu cạnh?
Đáp án: A Phương pháp giải: Quan sát hình vẽ. Lời giải chi tiết: Hình vẽ trên có 11 mặt và 20 canh. Chọn A. Câu hỏi 12 : Có bao nhiêu khối đa diện đều có các mặt là tam giác đều?
Đáp án: A Phương pháp giải: Sử dụng định nghĩa các khối đa diện đều. Lời giải chi tiết: Có 3 khối đa diện đều mà các mặt của nó là tam giác đều: tứ diện đều, bát diện đều và khối hai mươi mặt đều. Chọn A. Câu hỏi 13 : Cho hình chóp \(S.ABCD\) có đáy ABCDlà hình vuông. Biết hai mặt phẳng \(\left( SAB \right)\) và \(\left( SAD \right)\) cùng vuông góc với đáy. Hình chóp này có bao nhiêu mặt phẳng đối xứng ?
Đáp án: B Phương pháp giải: Mặt phẳng \(\left( \alpha \right)\) là mặt phẳng đối xứng của hình H khi mọi điểm thuộc hình H lấy đối xứng qua mặt phẳng \(\left( \alpha \right)\) đề thuộc hình H. Lời giải chi tiết: Biết hai mặt phẳng \(\left( SAB \right)\) và \(\left( SAD \right)\) cùng vuông góc với đáy nên\(SA\bot \left( ABCD \right)\) Ta thấy khối chóp \(S.ABCD\) có một mặt phẳng đối xứng là \(\left( SAC \right)\) Chọn B. Câu hỏi 14 : Hình đa diện bên có bao nhiêu cạnh ?
Đáp án: C Phương pháp giải: Quan sát hình vẽ và đếm số cạnh của hình. Lời giải chi tiết: Từ hình vẽ ta thấy hình đa diện bên có 15 cạnh. Chọn: C. Câu hỏi 15 : Hình nào dưới đây không phải hình đa diện?
Đáp án: C Phương pháp giải: Khái niệm: Hình đa diện (gọi tắt là đa diện) (H) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai điều kiện: 1) Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung. 2) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác. Lời giải chi tiết: Hình 3 vi phạm điều kiện 2) : Do trong Hình 3, tồn tại 1 cạnh là cạnh chung của 3 đa giáC. Chọn: C. Câu hỏi 16 : Hình đa diện nào dưới đây không có tâm đối xứng ?
Đáp án: C Phương pháp giải: Vẽ hình xác định tâm đối xứng. Lời giải chi tiết: Hình tứ diện đều không có tâm đối xứng. Chọn C Câu hỏi 17 : Trong các mệnh đề sau, mệnh đề nào đúng ?
Đáp án: D Phương pháp giải: Xét một vài hình đa diện thường gặp để thấy tính đúng sai Lời giải chi tiết: Hình lập phương có số mặt là 6 và số đỉnh là 4. Tứ diện có số đỉnh và số mặt bằng nhau, và bằng 4. Chọn D
Câu hỏi 18 : Khối lăng trụ ngũ giác có tất cả bao nhiêu cạnh ?
Đáp án: D Phương pháp giải: Vẽ khối lăng trụ ngũ giác, đếm số cạnh. Lời giải chi tiết: Một mặt đáy là 5 cạnh; số cạnh bên là 5 cạnh. Khối lăng trụ ngũ giác có tất cả \(2.5+5=15\) cạnh. Chọn D Câu hỏi 19 : Trong các mệnh đề sau, mệnh đề nào đúng ? Số các cạnh của hình đa diện luôn luôn …
Đáp án: A Phương pháp giải: Xét một khối đa diện bất kỳ để thấy tính đúng – sai của mệnh đề Lời giải chi tiết: Xét hình tứ diện có 6 cạnh nên số các cạnh của hình đa diện luôn luôn lớn hơn hoặc bằng 6 Chọn A Câu hỏi 20 : Hình tứ diện có bao nhiêu cạnh?
Đáp án: D Phương pháp giải: Sử dụng định nghĩa hình tứ diện. Lời giải chi tiết: Hình tứ diện có \(6\) cạnh. Chọn D. Câu hỏi 21 : Tìm số cạnh ít nhất của hình đa diện có 5 mặt.
Đáp án: D Phương pháp giải: Dựa vào lý thuyết về khối đa diện. Lời giải chi tiết: Mỗi mặt của đa diện có ít nhất 3 cạnh (khi mặt là tam giác) và mỗi cạnh của đa diện là cạnh chung của 2 mặt. Khi đó, một đa diện \(n\) mặt có ít nhất \(\frac{3n}{2}\) cạnh. Với \(n=5\) \(\Rightarrow \) Số cạnh \(\ge \,\,\frac{15}{3}=7,5.\) Vậy khối đa diện cần tìm có ít nhất 8 cạnh. Chọn D Câu hỏi 22 : Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng ?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hình hộp chữ nhật có ba kích thước khác nhau có 3 mặt phẳng đối xứng. Chọn B. Câu hỏi 23 : Khối đa diện sau có bao nhiêu mặt ?
Đáp án: A Phương pháp giải: Đếm các mặt của khối đa diện Lời giải chi tiết: Khối đa diện trên hình vẽ có tất cả 9 mặt. Chọn A Câu hỏi 24 : Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?
Đáp án: C Phương pháp giải: Dựa vào lý thuyết khối đa diện. Lời giải chi tiết: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất 3 mặt. Chọn: C Câu hỏi 25 : Một hình đa diện có các mặt là các tam giác thì số mặt \(M\) và số cạnh \(C\) của đa diện đó thỏa mãn hệ thức nào dưới đây?
Đáp án: C Phương pháp giải: Chọn một khối đa diện bất kì để tìm số mặt M, số cạnh C Lời giải chi tiết: Chọn tứ diện ABCD\(\Rightarrow \) \(\left\{ \begin{array}{l}M = 4\\C = 6\end{array} \right.3M = 2C.\) Chọn C Câu hỏi 26 : Trong các hình dưới đây, hình nào không phải là hình đa diện ?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 27 : Hình đa diện bên có bao nhiêu mặt?
Đáp án: C Phương pháp giải: Lời giải chi tiết: Câu hỏi 28 : Khối lăng trụ tam giác có bao nhiêu đỉnh?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Khối lăng trụ tam giác có 6 đỉnh. Chọn: A Câu hỏi 29 : Khối chóp ngũ giác có số cạnh là:
Đáp án: D Phương pháp giải: Lời giải chi tiết: Khối chóp ngũ giác có 10 cạnh. Chọn: D Câu hỏi 30 : Số hình đa diện lồi trong các hình dưới đây là:
Đáp án: C Phương pháp giải: Khối đa diện \(\left( H \right)\) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của \(\left( H \right)\) luôn thuộc \(\left( H \right)\). Khi đó đa diện giới hạn \(\left( H \right)\) được gọi là đa diện lồi. Một khối đa diện là đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó. Lời giải chi tiết:
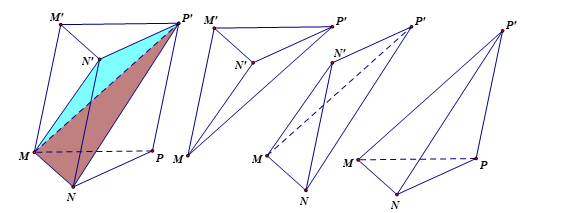
Chỉ có khối đa diện cuối cùng là đa diện lồi. Chọn đáp án C. Câu hỏi 31 : Cắt khối lăng trụ \(MNP.M'N'P'\) bởi các mặt phẳng \(\left( {MN'P'} \right)\) và \(\left( {MNP'} \right)\) ta được những khối đa diện nào?
Đáp án: A Phương pháp giải: Phân chia và lắp ghép các khối đa diện. Lời giải chi tiết:
Dựa vào hình vẽ ta chọn đáp án \({\bf{A}}\). Chọn A. Câu hỏi 32 : Cho hình chóp có 20 cạnh. Tính số mặt của hình chóp đó.
Đáp án: B Phương pháp giải: +) Hình chóp có đáy là đa giác đáy n cạnh thì có \(n+1\) đỉnh, có \(n+1\) mặt và có \(2n\) cạnh. +) Theo hệ thức Ơ-le ta có: Số đỉnh + Số mặt = Số cạnh +2. Lời giải chi tiết: Giả sử hình chóp có đa giác đáy n cạnh \(\Rightarrow \) hình chóp có \(n+1\) đỉnh, \(n+1\) mặt và \(2n\) cạnh. Theo hệ thức Ơ-le ta có: Số đỉnh + Số mặt = Số cạnh + 2. \(\begin{align} & \Rightarrow n+1+n+1=20+2 \\ & \Leftrightarrow 2n=20 \\ & \Leftrightarrow n=10. \\ \end{align}\) Vậy hình chóp có 11 mặt. Chọn B. Câu hỏi 33 : Một hình lăng trụ có 2018 mặt. Hỏi hình lăng trụ đó có tất cả bao nhiêu cạnh?
Đáp án: C Phương pháp giải: Áp dụng Hệ thức Euleur có: \(D+M=C+2\) Lời giải chi tiết: Gọi số cạnh của 1 đáy của hình lăng trụ là n cạnh, nên số cạnh đáy của hình lăng trụ (2 mặt đáy) là 2n cạnh. Số cạnh bên là n cạnh. Tổng số cạnh của lăng trụ là 3n cạnh. Lại có Đ + M = C + 2 Nên:2n + 2018 = 3n + 2 n= 2016 Vây số cạnh của hình lăng trụ là 3.2016 = 6048 (cạnh) Chọn C Câu hỏi 34 : Cho lăng trụ đứng \(ABCD.{A}'{B}'{C}'{D}'\) có đáy là hình thoi (không phải hình vuông). Phát biểu nào sau đây sai ?
Đáp án: C Phương pháp giải: Dựng hình, xác định tâm và các mặt phẳng đối xứng của hình lăng trụ đứng Lời giải chi tiết: Dựa vào đáp án, ta thấy rằng: Bốn mặt bên của hình lăng trụ đã cho là các hình chữ nhật bằng nhau \(\Rightarrow \) A đúng. Trung điểm của đường chéo \(A{C}'\) là tâm đối xứng của hình lăng trụ \(\Rightarrow \) B đúng. Hình lăng trụ đã cho có 3 mặt phẳng đối xứng \(\Rightarrow \) C sai. Thể tích khối lăng trụ đã cho là \({{V}_{ABCD.{A}'{B}'{C}'{D}'}}=B{B}'.{{S}_{{A}'{B}'{C}'{D}'}}\) \(\Rightarrow \) D đúng. Chọn C. Câu hỏi 35 : Khối đa diện bên dưới có bao nhiêu đỉnh?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Câu hỏi 36 : Số mặt phẳng đối xứng của hình lăng trụ đứng có đáy là hình vuông là:
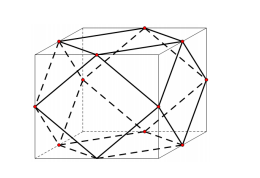
Đáp án: C Phương pháp giải: Dựa vào khái niệm mặt phẳng đối xứng. Lời giải chi tiết: Hình lăng trụ đứng có đáy là hình vuông có 4 mặt phẳng đối xứng cắt theo chiều dọc và 1 mặt phẳng cắt theo chiều ngang. Chọn đáp án C. Câu hỏi 37 : Người ta nối trung điểm các cạnh của hình hộp chữ nhật rồi cắt bỏ các hình chóp tam giác ở các góc của hình hộp như hình vẽ bên. Hình còn lại là một đa diện có số đỉnh và số cạnh là:
Đáp án: A Phương pháp giải: Tính số cạnh và số đỉnh nằm trên một mặt của hình hộp chữ nhật. Lời giải chi tiết:
Hình hộp chữ nhật có tất cả 12 cạnh \( \Rightarrow \) Số đỉnh của hình cần biết là 12 đỉnh \( \Rightarrow \) Loại B, C. Mỗi mặt của hình hộp chữ nhật chứa 4 cạnh của hình cần biết mà hình hộp chữ nhật có 6 mặt \( \Rightarrow \) Số cạnh của hình cần biết là 24 cạnh. Chọn A. Câu hỏi 38 : Số mặt phẳng đối xứng của khối lăng trụ tam giác đều là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Ta có các mặt đối xứng của khối lăng trụ tam giác đều là các mặt phẳng trung trực của các đoạn thẳng \(AB,BC,CA,AA'\). Chọn: B Câu hỏi 39 : Tổng diện tích tất cả các mặt của hình tứ diện đều cạnh a bằng:
Đáp án: C Phương pháp giải: Tứ diện đều có 4 mặt đều là tam giác đều. Lời giải chi tiết: Tổng diện tích tất cả các mặt của hình tứ diện đều cạnh a bằng: \(4.\dfrac{{{a^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \). Chọn: C Câu hỏi 40 : Cho một hình đa diện. Khẳng định nào sau đây sai ?
Đáp án: D Phương pháp giải: Sử dụng khái niệm: Khối đa diện là hình gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện: +) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có 1 cạnh chung. +) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác. Lời giải chi tiết: Sử dụng khái niệm: Khối đa diện là hình gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện: +) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có 1 cạnh chung. +) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác. Vậy đáp án sai là D. Chọn D. Câu hỏi 41 : Tính tổng số đo các góc ở tất cả các mặt của hình chóp ngũ giác?
Đáp án: D Phương pháp giải: Tính tổng số đo của các góc ở từng mặt sau đó cộng tổng lại ta được tổng số đo của tất cả các góc trong hình chóp ngũ giác. Đa giác có \(n\) đỉnh thì có tổng số đo các góc là \(\left( {n - 2} \right)\pi .\) Lời giải chi tiết: Hình chóp ngũ giác có mặt đáy là hình ngũ giác, có tổng số đo các góc là \(\left( {5 - 2} \right)\pi = 3\pi \)và 5 mặt bên, mỗi mặt bên là một tam giác có số đo các góc là \(\pi .\) Do đó tổng số đo tất cả các góc của hình chóp ngũ giác là \(3\pi + 5\pi = 8\pi .\) Chọn D. Câu hỏi 42 : Hình nào dưới đây có nhiều mặt phẳng đối xứng nhất?
Đáp án: C Phương pháp giải: Tìm số mặt phẳng đối xứng của từng hình để so sánh. Lời giải chi tiết: Mặt phẳng đối xứng của tứ diện đều là mặt phẳng đi qua 1 đỉnh và trung tuyến của mặt đối diện. Như vậy tứ diện đều có 6 mặt phẳng đối xứng - Lăng trụ tam giác đều có 3 mặt phẳng đối xứng đi qua trung tuyến của tam giác đáy và vuông góc với đáy và 1 mặt phẳng đối xứng đi qua các trung điểm cạnh bên - Hình lập phương \(ABCD.A'B'C'D'\) có \(M,N,P,Q,M',N',P',Q'\) lần lượt là trung điểm các cạnh \(AB,BC,CD,DA,A'B',B'C',C'D',D'A'\) có 9 mặt phẳng đối xứng là \(\left( {ABC'D'} \right),\left( {BCD'A'} \right),\left( {CDA'B'} \right),\left( {DAB'C'} \right),\left( {ACC'A'} \right),\left( {BDD'B'} \right),\left( {MPP'M'} \right),\left( {NQQ'N} \right)\) và 1 mặt phẳng đi qua trung điểm các cạnh bên. - Hình chóp tứ giác đều có 4 mặt phẳng đối xứng. Vậy hình lập phương có nhiều mặt phẳng đối xứng nhất. Chọn C. Câu hỏi 43 : Hình chóp có 22 cạnh thì có bao nhiêu mặt ?
Đáp án: B Phương pháp giải: - Tính số cạnh đáy. - Tổng số mặt bằng số mặt bên cộng mặt đáy. Lời giải chi tiết: Gọi số cạnh của đáy là \(n\,\,\left( {n \in {\mathbb{N}^*}} \right)\)\( \Rightarrow \) Đáy của chóp là \(n - \) giác. Ứng với mỗi đỉnh của đáy của 1 cạnh nối đỉnh của hình chóp với đỉnh của chóp. Suy ra hình chóp có tổng số cạnh là \(2n\). Theo bài ra ta có: \(2n = 22 \Rightarrow n = 11\,\,\,\left( {tm} \right).\) Do đó hình chóp đáy là 11 – giác. Do đó chóp có 11 mặt bên + 1 đáy. Vậy hình chóp có tổng 12 mặt. Chọn B. Câu hỏi 44 : Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng ?
Đáp án: A Phương pháp giải: Dựng hình và đếm số mặt phẳng đối xứng. Lời giải chi tiết: Hình chóp tứ giác đều có \(4\) mặt phẳng đối xứng. Chọn A. Câu hỏi 45 : Lăng trụ đứng có đáy là ngũ giác đều có số mặt phẳng đối xứng bằng
Đáp án: B Phương pháp giải: Sử dụng lý thuyết khối đa diện để làm bài. Lời giải chi tiết: Lăng trụ đứng ngũ giác đều có 1 mặt phẳng đối xứng ngang (đi qua trung điểm các cạnh bên) và 5 mặt phẳng đối xứng đứng (ứng với 5 trục đối xứng của đáy). Chọn B. Câu hỏi 46 : Hình lăng trụ có thể có số cạnh nào sau đây ?
Đáp án: A Phương pháp giải: Số cạnh của lăng trụ có đáy là \(n - \) giác là \(3n\). Lời giải chi tiết: Giả sử hình lăng trụ có đáy là \(n - \)giác. Khi đó, số cạnh của lăng trụ là: \(3n\) Suy ra, trong các đáp án trên, số cạnh của hình lăng trụ chỉ có thể là 2019 (Vì \(2019\,\, \vdots \,\,3\)). Chọn A. Câu hỏi 47 : Trong các mệnh đề sau, mệnh đề nào đúng ?
Đáp án: D Phương pháp giải: Xét một vài hình đa diện thường gặp để thấy tính đúng sai Lời giải chi tiết: Hình lập phương có số mặt là 6 và số đỉnh là 4. Tứ diện có số đỉnh và số mặt bằng nhau, và bằng 4. Chọn D
Câu hỏi 48 : Trong các lăng trụ sau, lăng trụ nào không nội tiếp được trong một mặt cầu?
Đáp án: C Phương pháp giải: Các tứ giác có thể nội tiếp đường tròn là: hình chữ nhật, hình vuông, hình thang cân. Lời giải chi tiết: Các tứ giác có thể nội tiếp đường tròn là: hình chữ nhật, hình vuông, hình thang cân. Chọn C. Câu hỏi 49 : Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất
Đáp án: D Phương pháp giải: Sử dụng khái niệm hình đa diện. Lời giải chi tiết: Mỗi đỉnh của 1 hình đa diện là đỉnh chung của ít nhất 3 cạnh. Chọn D. Câu hỏi 50 : Biết các hình dưới đây tạo thành từ hữu hạn các đa giác. Hình nào là hình đa diện.
Đáp án: B Phương pháp giải: Lời giải chi tiết: Chọn B. |














 Chọn C.
Chọn C.