Phương pháp giải:

- Bất đẳng thức Cauchy cho 2 số x, y không âm: \(\frac{{x + y}}{2} \ge \sqrt {xy} \,\,\forall x,y \ge 0.\)

Dấu “=” xảy ra khi và chỉ khi x = y.

Lời giải chi tiết:

Ta có: \(x + \frac{5}{{x - 2}} = x - 2 + \frac{5}{{x - 2}} + 2\)

Vì x > 2 nên x – 2 > 0 và \(\frac{5}{{x - 2}} > 0\) Áp dụng bất đẳng thức Cauchy cho 2 số x – 2 và \(\frac{5}{{x - 2}}\) ta có: 

\(\begin{array}{l}x - 2 + \frac{5}{{x - 2}} \ge 2\sqrt {\left( {x - 2} \right)\frac{5}{{x - 2}}} = 2\sqrt 5 \\ \Rightarrow x + \frac{5}{{x - 2}} = x - 2 + \frac{5}{{x - 2}} + 2 \ge 2\sqrt 5 + 2\end{array}\) 

Vậy \(\min f\left( x \right) = 2\sqrt 5  + 2\). Dấu “=” xảy ra khi 

\(x - 2 = \frac{5}{{x - 2}} \Leftrightarrow {\left( {x - 2} \right)^2} = 5 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 5 \\x = 2 - \sqrt 5 \end{array} \right.\)

Chọn C.

Phương pháp giải:

Suy luận, kết hợp sử dụng định nghĩa và tính chất của bất đẳng thức.

Lời giải chi tiết:

A.\(a + c > b + d\) đúng. Vì cộng vế với vế hai bất đẳng thức cùng chiều ta được bất đẳng thức cùng chiều.

D. \(ac > bd\) đúng. Vì sử dụng tính chất cơ bản\(a > b > 0;\,c > d > 0 \Rightarrow ac > bd\(.

C. \({a \over b} > {d \over c}\) đúng. Vì từ \(ac > bd \Rightarrow {{ac} \over {bc}} > {{bd} \over {bc}} \Rightarrow {a \over b} > {d \over c}\).

B.  \({a \over c} > {b \over d}\) sai. Vì giả sử chọn \(a = c > 0\) và \(b = d > 0\) thỏa mãn giả thiết, nhưng \({a \over c} = {b \over d} = 1\).

Chọn B.

Phương pháp giải:

Sử dụng phương pháp loại trừ.

Lời giải chi tiết:

Đáp án A: \(\left\{ \matrix{  a < 1 \hfill \cr   b < 1 \hfill \cr}  \right. \Rightarrow ab < 1\), suy luận không đúng. Ví dụ \(\left\{ \matrix{   - 3 < 1 \hfill \cr   - 2 < 1 \hfill \cr}  \right. \Rightarrow \left( { - 3} \right)\left( { - 2} \right) = 6 > 1\)

Đáp án B: \(\left\{ \matrix{  a < 1 \hfill \cr   b < 1 \hfill \cr}  \right. \Rightarrow a - b < 1\), suy luận không đúng. Ví dụ \(\left\{ \matrix{  0 < 1 \hfill \cr    - 2 < 1 \hfill \cr}  \right. \Rightarrow 0 - \left( { - 2} \right) = 2 > 1\)

Đáp án C: \(\left\{ \matrix{  a < 1 \hfill \cr   b < 1 \hfill \cr}  \right. \Rightarrow {a \over b} < 1\), suy luận không đúng. Ví dụ \(\left\{ \matrix{   - 3 < 1 \hfill \cr   - 2 < 1 \hfill \cr}  \right. \Rightarrow {{ - 3} \over { - 2}} = {3 \over 2} > 1\)

Đáp án D: \(\left\{ \matrix{  0 < a < 1 \hfill \cr   b < 1 \hfill \cr}  \right. \Rightarrow ab < 1\), là suy luận đúng. Vì, ta xét hai trường hợp:

Nếu \(b \le 0\) thì \(ab \le 0\), hiển nhiên \(ab < 1\)

Nếu \(b > 0\) ta có \(\left\{ \matrix{  0 < a < 1 \hfill \cr   0 < b < 1 \hfill \cr}  \right. \Rightarrow ab < 1\) suy luận đúng. (tính chất cơ bản)

Chọn D.

Phương pháp giải:

Sử dụng các tính chất cơ bản của bất đẳng thức để đánh giá biểu thức P.

Lời giải chi tiết:

Ta có: \(P = {a \over {a + b}} + {b \over {b + c}} + {c \over {c + a}}>{a \over {a + b + c}} + {b \over {a + b + c}} + {c \over {a + b + c}} = {{a + b + c} \over {a + b + c}} = 1\) (1)

Mặt khác, ta có

\(0 < {a \over {a + b}} < 1 \Rightarrow {a \over {a + b}} < {{a + c} \over {a + b + c}}\)

Tương tự, ta có:

\(0 < {b \over {b + c}} < 1 \Rightarrow {b \over {b + c}} < {{a + b} \over {a + b + c}}\)

\(0 < {c \over {c + a}} < 1 \Rightarrow {c \over {c + a}} < {{b + c} \over {b + c + a}}\)

Cộng vế với vế ba bất đẳng thức trên ta có:

\(P < {{a + c} \over {a + b + c}} + {{a + b} \over {a + b + c}} + {{b + c} \over {b + c + a}} = {{2\left( {a + b + c} \right)} \over {a + b + c}} = 2\,\,\,\,\left( 2 \right)\)

Kết hợp (1) và (2) có \(1 < P < 2\)

Chọn A.

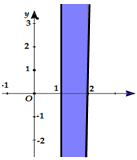
Phương pháp giải:

Sử dụng phương pháp biến đổi tương đương để biến đổi bất đẳng thức.

Lời giải chi tiết:

\(\begin{array}{l}\frac{{{a^2} + {b^2}}}{2} \le {\left( {\frac{{a + b}}{2}} \right)^2} \Leftrightarrow \frac{{{a^2} + {b^2}}}{2} \le \frac{{{a^2} + {b^2} + 2ab}}{4} \Leftrightarrow \frac{{2{a^2} + 2{b^2}}}{4} - \frac{{{a^2} + {b^2} + 2ab}}{4} \le 0\\ \Leftrightarrow \frac{{{a^2} + {b^2} - 2ab}}{4} \le 0 \Leftrightarrow {\left( {a - b} \right)^2} \le 0 \Leftrightarrow a - b = 0 \Leftrightarrow a = b\end{array}\)

Chọn C.

Phương pháp giải:

Nhìn hình vẽ để xác định bất phương trình.

Lời giải chi tiết:

Phần tô đậm trong hình vẽ dưới đây (có chứa biên), biểu diễn tập nghiệm của bất phương trình \(1 \le x \le 2\)

Chọn C.

Phương pháp giải:

Áp dụng BĐT Cô-si đánh giá mẫu thức.

Lời giải chi tiết:

Áp dụng BĐT Cô-si ta có \({x^2} + 4 \ge 2\sqrt {{x^2}.4}  = 4x\) (Do \(x > 0\))

\( \Rightarrow f\left( x \right) \le \dfrac{x}{{4x}} = \dfrac{1}{4}\).

Dấu "=" xảy ra \( \Leftrightarrow {x^2} = 4 \Leftrightarrow x = 2\).

Vậy \(\max f\left( x \right) = \dfrac{1}{4} \Leftrightarrow x = 2 \Rightarrow M = \dfrac{1}{4}\).

Chọn A.

Phương pháp giải:

Sử dụng BĐT Cô-si cho hai số \(x,y \ge 0:\,\,x + y \ge 2\sqrt {xy} \). Dấu "=" xảy ra \( \Leftrightarrow x = y\).

Lời giải chi tiết:

Ta có: \(f\left( x \right) = \dfrac{{{x^2} + 5}}{{\sqrt {{x^2} + 4} }} = \dfrac{{{x^2} + 4 + 1}}{{\sqrt {{x^2} + 4} }} = \sqrt {{x^2} + 4}  + \dfrac{1}{{\sqrt {{x^2} + 4} }}\)

Áp dụng BĐT Cô-si cho 2 số dương \(\sqrt {{x^2} + 4} ,\,\,\dfrac{1}{{\sqrt {{x^2} + 4} }}\) ta có:

\(\sqrt {{x^2} + 4}  + \dfrac{1}{{\sqrt {{x^2} + 4} }} \ge 2\sqrt {\sqrt {{x^2} + 4} .\dfrac{1}{{\sqrt {{x^2} + 4} }}}  = 2 \Rightarrow f\left( x \right) \ge 2\).

Dấu “=” xảy ra \( \Leftrightarrow \sqrt {{x^2} + 4}  = \dfrac{1}{{\sqrt {{x^2} + 4} }} \Leftrightarrow {x^2} + 4 = 1 \Leftrightarrow {x^2} =  - 3\) (Vô lí)

Vậy hàm số đã cho không có giá trị nhỏ nhất.

Chọn D.

Phương pháp giải:

Nhóm hạng tử, áp dụng bất đẳng thức hệ quả của bất đẳng thức Cosi để tìm min

Lời giải chi tiết:

Từ giả thiết \(x+y+xy\ge 7\Leftrightarrow 2\left( x+1 \right)\left( y+1 \right)\ge 16.\)

Ta có \(16\le 2\left( x+1 \right)\left( y+1 \right)=\left( x+1 \right)\left( 2y+2 \right)\le {{\left( \frac{1+x+2y+2}{2} \right)}^{2}}\)

\(\Leftrightarrow {{\left( x+2y+3 \right)}^{2}}\ge 64\Leftrightarrow \left[ \begin{align}  x+2y\ge 5 \\  x+2y\le -11 \\ \end{align} \right.\Leftrightarrow x+2y\ge 5\) (do \(x,y>0\)).

Chọn B

Phương pháp giải:

Áp dụng hệ quả của bất đẳng thức Cosi cho 2 số dương \(ab\le \frac{{{a}^{2}}+{{b}^{2}}}{4}\)

Lời giải chi tiết:

Áp dụng bất đẳng thức hệ quả của Côsi \(ab\le \frac{{{\left( a+b \right)}^{2}}}{4},\) ta được

\(f\left( x \right)=3\left( 2x+1 \right)\left( 5-2x \right)\le 3.\frac{{{\left( 2x+1+5-2x \right)}^{2}}}{4}=27\Rightarrow f\left( x \right)\le 27.\)

Dấu \(''\,\,=\,\,''\) xảy ra \(\Leftrightarrow \left\{ \begin{align}  -\frac{1}{2}\le x\le \frac{5}{2} \\  2x+1=5-2x \\ \end{align} \right.\Leftrightarrow x=1.\) Vậy \(M=27.\)

Chọn C

Phương pháp giải:

Sử dụng bất đẳng thức chuyển từ “trung bình nhân” sang “trung bình cộng”:  \(abc\le {{\left( \dfrac{a+b+c}{3} \right)}^{3}}\)

Để làm triệt tiêu được biến thì ta cần nhân thêm hệ số thích hợp.

Lời giải chi tiết:

\(\begin{array}{l}A = \left( {x - 5} \right)\left( {3y - 6} \right)\left( {x + 3y} \right)\\\,\,\,\,\, = \left( {5 - x} \right)\left( {6 - 3y} \right)\left( {x + 3y} \right) \le {\left[ {\dfrac{{\left( {5 - x} \right) + \left( {6 - 3y} \right) + \left( {x + 3y} \right)}}{3}} \right]^3}\\3A \le {\left( {\dfrac{{11}}{3}} \right)^3} \Leftrightarrow 3A \le \dfrac{{1331}}{{27}} \Rightarrow \,Max\,A = \dfrac{{1331}}{{81}}\\ \Leftrightarrow 5 - x = 6 - 3y = x + 3y\\ \Leftrightarrow \left\{ \begin{array}{l}5 - x = 6 - 3y\\5 - x = x + 3y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - x + 3y = 1\\ - 2x - 3y =  - 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 3x =  - 4\\ - x + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{4}{3}\\y = \dfrac{7}{9}\end{array} \right.\end{array}\)

Chọn A.

Phương pháp giải:

Áp dụng bất đẳng thức Bunhia-cốp-ski:

Với 2 bộ số \((a,b)\)và \(\left( x,y \right)\)ta có: \({{\left( a\,x+b\,y \right)}^{2}}\le \left( {{a}^{2}}+{{b}^{2}} \right)\left( {{x}^{2}}+{{y}^{2}} \right)\)

Lời giải chi tiết:

Ta có:

+) \({{a}^{2}}+{{b}^{2}}=\frac{1}{2}\left( {{1}^{2}}+{{1}^{2}} \right)\left( {{a}^{2}}+{{b}^{2}} \right)\ge \frac{1}{2}{{\left( a+b \right)}^{2}}=\frac{1}{2}{{.2}^{2}}=2\). Suy ra mệnh đề đáp án B đúng

 +) \({{a}^{4}}+{{b}^{4}}=\frac{1}{2}\left( {{1}^{2}}+{{1}^{2}} \right)\left[ {{\left( {{a}^{2}} \right)}^{2}}+{{\left( {{b}^{2}} \right)}^{2}} \right]\ge \frac{1}{2}{{\left( {{a}^{2}}+{{b}^{2}} \right)}^{2}}\ge \frac{1}{2}{{.2}^{2}}=2\). Suy ra mệnh đề đáp án A đúng và mệnh đề đáp án C sai.

Chọn C

Hiển nhiên mệnh đề D đúng theo bất đẳng thức Cauchy.

Phương pháp giải:

Áp dụng bất đẳng thức Bunhia-cốp-ski:

Với 2 bộ số \((a,b,c)\)và \(\left( x,y,z \right)\)ta có: \({{\left( a\,x+b\,y+cz \right)}^{2}}\le \left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)\left( {{x}^{2}}+{{y}^{2}}+{{z}^{2}} \right)\)

Lời giải chi tiết:

Áp dụng bất đẳng thức Bunhia-cốp-ski:

Với 2 bộ số \((x,y,z)\)và \(\left( y,z,x \right)\)ta có: \({{\left( x.y+y.z+z.x \right)}^{2}}\le \left( {{x}^{2}}+{{y}^{2}}+{{z}^{2}} \right)\left( {{y}^{2}}+{{z}^{2}}+{{x}^{2}} \right)\)

\(\Leftrightarrow {{\left( x.y+y.z+z.x \right)}^{2}}\le {{\left( {{x}^{2}}+{{y}^{2}}+{{z}^{2}} \right)}^{2}}\)

Theo giả thiết \(xy+yz+zx=4\) nên ta có \({{\left( {{x}^{2}}+{{y}^{2}}+{{z}^{2}} \right)}^{2}}\ge 16\) hay \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}\ge 4\)(*)

Với 2 bộ số \((1,1,1)\)và \(\left( {{x}^{2}},{{y}^{2}},{{z}^{2}} \right)\)ta có: \({{\left( 1.{{x}^{2}}+1.{{y}^{2}}+1.{{z}^{2}} \right)}^{2}}\le \left( {{1}^{2}}+{{1}^{2}}+{{1}^{2}} \right)\left( {{x}^{4}}+{{y}^{4}}+{{z}^{4}} \right)\)

Suy ra: \({{x}^{4}}+{{y}^{4}}+{{z}^{4}}\ge \frac{{{\left( {{x}^{2}}+{{y}^{2}}+{{z}^{2}} \right)}^{2}}}{3}\)

Từ (*), suy ra \({{x}^{4}}+{{y}^{4}}+{{z}^{4}}\ge \frac{16}{3}\)

Chọn B.

Phương pháp giải:

Với \(a,b\)là hai số dương ta có bất đẳng thức: \(\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}\) hay \(\frac{1}{a+b}\le \frac{1}{4}\left( \frac{1}{a}+\frac{1}{b} \right)\)(*)

Lời giải chi tiết:

Áp dụng bất đẳng thức (*) ta có : \(\frac{1}{a+b}\le \frac{1}{4}\left( \frac{1}{a}+\frac{1}{b} \right)\)

Tương tự ta có : \(\frac{1}{b+c}\le \frac{1}{4}\left( \frac{1}{b}+\frac{1}{c} \right);\,\,\frac{1}{a+c}\le \frac{1}{4}\left( \frac{1}{a}+\frac{1}{c} \right)\)

Cộng vế với vế ta có : \(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}\le \frac{1}{2}\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\)

Chọn A.

Phương pháp giải:

Suy luận, kết hợp sử dụng định nghĩa và tính chất của bất đẳng thức.

Lời giải chi tiết:

Từ giả thiết \(m > 0\)  và \(n < 0\) suy ra \(m > 0\)  và \( - n > 0\). Cộng vế với vế của hai bất đẳng thức cùng dấu ta có: \(m - n > 0\)  hay \(n - m < 0\).

Chọn B.

Phương pháp giải:

Suy luận, kết hợp sử dụng định nghĩa và tính chất của bất đẳng thức.

Lời giải chi tiết:

Đáp án A: \(10x > 3x\) chỉ đúng khi \(x > 0\). Loại A

Đáp án B: \(10{x^2} > 3{x^2}\) chỉ đúng khi \(x \ne 0\). Loại B

Đáp án C: Xuất phát từ bất đẳng thức đúng \(10 > 3\), cộng hai vế với cùng một số \( - x\) ta được một bất đẳng thức đúng (tính chất cơ bản). Chọn C

Đáp án D: \(3 + x > 10 - x \Leftrightarrow 2x > 7 \Leftrightarrow x > {7 \over 2}\). Loại D

Chọn C.

Phương pháp giải:

Suy luận, kết hợp sử dụng định nghĩa và tính chất của bất đẳng thức.

Lời giải chi tiết:

A. \(a - c > b - d\). Không có tính chất trừ vế với vế của hai bất đẳng thức cùng chiều ta được một bất đẳng thức mới cùng chiều.

B. \({a \over c} > {b \over d}\) sai trong một số trường hợp. Ví dụ \(a = 4,b = 2,c = 3,d = 1\).

C. \(ac > bd\) chỉ đúng khi có \(a > b > 0\) và \(c > d > 0\)

D. \(a + c > b + d\) đúng. Vì cộng vế với vế của hai bất đẳng thức cùng chiều ta được một bất đẳng thức mới cùng chiều. (tính chất cơ bản)

Chọn D.

Phương pháp giải:

Áp dụng bất đẳng thức Cauchy cho hai số dương 

Lời giải chi tiết:

Áp dụng bất đẳng thức Cauchy cho hai số dương \(x,y\) ta có : \(x + y \ge 2\sqrt {xy}  = 2.\sqrt {36}  = 12\)

Áp dụng bất đẳng thức Cauchy cho hai số dương \({x^2},{y^2}\) ta có : \({x^2} + {y^2} \ge 2\sqrt {{x^2}.{y^2}}  = 2|xy| = 2xy = 72\)

Chọn A.

Phương pháp giải:

Áp dụng bất đẳng thức Cauchy cho hai số dương \(2x;{1 \over x}\)

Lời giải chi tiết:

Áp dụng bất đẳng thức Cauchy cho hai số dương ta có: \(f(x) = 2x + {1 \over x} \ge 2\sqrt {2x.{1 \over x}}  = 2\sqrt 2 \).

Chọn A.

Phương pháp giải:

Biến đổi tương đương bất đẳng thức đã cho.

Lời giải chi tiết:

\(\eqalign{ & {\left( {m + n} \right)^2} \ge 4mn \Leftrightarrow {m^2} + 2mn + {n^2} \ge 4mn \Leftrightarrow {m^2} + 2mn + {n^2} - 4mn \ge 0  \cr   &  \Leftrightarrow {m^2} - 2mn + {n^2} \ge 0 \Leftrightarrow {m^2} + {n^2} \ge 2mn \cr} \)

Chọn B.

Phương pháp giải:

Sử dụng biến đổi tương đương và sử dụng bất đẳng thức Cauchy cho hai số không âm.

Lời giải chi tiết:

Ta có: \(\left( {{\rm{ax}} + by} \right)\left( {bx + ay} \right) = ab{x^2} + {a^2}xy + {b^2}xy + ab{y^2} = \left( {{x^2} + {y^2}} \right)ab + {a^2}xy + {b^2}xy\).

Áp dụng bất đẳng thức Cauchy cho hai số không âm \({x^2},{y^2}\) ta có: \({x^2} + {y^2} \ge 2xy\).

Mặt khác, \(a;b\) là các số không âm nên \(ab \ge 0\). Do đó, ta có

 \(\left( {{x^2} + {y^2}} \right)ab + {a^2}xy + {b^2}xy \ge 2xy.ab + {a^2}xy + {b^2}xy = {\left( {a + b} \right)^2}xy\)

Suy ra ta có: \(\left( {{\rm{ax}} + by} \right)\left( {bx + ay} \right) \ge {\left( {a + b} \right)^2}xy\).

Chọn A.

Phương pháp giải:

Áp dụng bất đẳng thức Cauchy cho 3 số dương \(a,b,c\) và áp dụng bất đẳng thức Cauchy cho 3 số dương \(a + b,b + c,c + a\).

Lời giải chi tiết:

Áp dụng bất đẳng thức Cauchy cho 3 số dương \(a,b,c\) ta có : \(abc \le {\left( {{{a + b + c} \over 3}} \right)^3}\).

Áp dụng bất đẳng thức Cauchy cho 3 số dương \(a + b,b + c,c + a\) ta có : \(\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) \le {\left( {{{2a + 2b + 2c} \over 3}} \right)^3}\).

Nhân vế với vế ta có

\(S = abc\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) \le {\left( {{{a + b + c} \over 3}} \right)^3}.{\left( {{{2a + 2b + 2c} \over 3}} \right)^3} = {\left( {{1 \over 3}} \right)^3}.{\left( {{2 \over 3}} \right)^3} = {{{{1.2}^3}} \over {{3^3}{{.3}^3}}} = {8 \over {729}}\)

Chọn A.

Phương pháp giải:

Áp dụng bất đẳng thức Cauchy cho hai số dương 

Lời giải chi tiết:

Áp dụng bất đẳng thức Cauchy cho hai số dương \(x,y\) ta có: \(x + y \ge 2\sqrt {xy}  \Leftrightarrow 12 \ge 2.\sqrt {xy}  \Leftrightarrow 6 \ge \sqrt {xy} \)

Suy ra \(\sqrt {xy}  \le 6\), suy ra \(xy \le 36\)

Chọn A.

Phương pháp giải:

Suy luận, kết hợp sử dụng định nghĩa và tính chất của bất đẳng thức.

Lời giải chi tiết:

A. \(ac > bc\) chỉ đúng khi có \(c > 0\)

B. \({a^2} < {b^2}\) chỉ đúng khi \(0 > a > b\)

C. \(a + c > b + c\) đúng. Vì cộng hai vế của bất đẳng thức với cùng một số hạng ta được một bất đẳng thức mới cùng chiều (tính chất cơ bản)

D. \(c - a > c - b\) sai. Vì \(a > b\) suy ra \( - a <  - b\). Suy ra \(c - a < c - b\).

Chọn C.

Phương pháp giải:

Áp dụng bất đẳng thức Bunhia-cốp-ski:

Với 2 bộ số \((a,b)\)và \(\left( x,y \right)\)ta có: \({{\left( a\,x+b\,y \right)}^{2}}\le \left( {{a}^{2}}+{{b}^{2}} \right)\left( {{x}^{2}}+{{y}^{2}} \right)\)

Lời giải chi tiết:

Áp dụng bất đẳng thức Bunhia-cốp-ski:

Với 2 bộ số \((1,1)\)và \(\left( \sqrt{x-2},\sqrt{4-x} \right)\)ta có: \({{\left( 1.\sqrt{x-2}+1.\sqrt{4-x} \right)}^{2}}\le \left( {{1}^{2}}+{{1}^{2}} \right)\left[ {{\left( \sqrt{x-2} \right)}^{2}}\text{+}{{\left( \sqrt{4-x} \right)}^{2}} \right]\)

Hay \({{A}^{2}}\le 2\left( x-2+4-x \right)=2.2=4\). Suy ra \(A\le 2\)

Dấu “=” xảy ra khi \(x=3\)

Mặt khác ta có \({{A}^{2}}=2+2\sqrt{\left( x-2 \right)\left( 4-x \right)}\ge 2\Rightarrow A\ge \sqrt{2}\)

Dấu “=” xảy ra khi \(x=4\) hoặc \(x=2\)

Chọn C.

Phương pháp giải:

Sử dụng bất đẳng thức: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge \frac{9}{a+b+c}\)với \(a,b\)\(,c\)   là hai số dương.

Lời giải chi tiết:

Với 3 số dương \(a,b,c\) có tổng bằng 1.

Áp dụng bất đẳng thức: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge \frac{9}{a+b+c}\)

Ta có: \(T=\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\ge \frac{9}{\left( a+b \right)+\left( b+c \right)+\left( c+a \right)}=\frac{9}{2\left( a+b+c \right)}\)

Vì \(a+b+c=1\)nên \(\frac{9}{2(a+b+c)}=\frac{9}{2}\). Suy ra \(T\ge \frac{9}{2}\)

Chọn D.

Phương pháp giải:

Sử dụng bất đẳng thức: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge \frac{9}{a+b+c}\)với \(a,b\)\(,c\)   là hai số dương.

Lời giải chi tiết:

Với \(a,b,c\) là 3 số thực không âm thỏa mãn điều kiện \(a+b+c\le 1\)

Áp dụng bất đẳng thức: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge \frac{9}{a+b+c}\)

Ta có: \(\frac{1}{{{a}^{2}}+2bc}+\frac{1}{{{b}^{2}}+2ca}+\frac{1}{{{c}^{2}}+2ab}\ge \frac{9}{{{a}^{2}}+2bc+{{b}^{2}}+2ca+{{c}^{2}}+2ab}=\frac{9}{{{\left( a+b+c \right)}^{2}}}\)

Vì \(a+b+c\le 1\)nên \(\frac{9}{{{\left( a+b+c \right)}^{2}}}\ge 9\Rightarrow S\ge 9\)

Chọn A.

Phương pháp giải:

Sử dụng bất đẳng thức: \(\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}\)với \(a,b\)là hai số dương.

Lời giải chi tiết:

Với hai số thực dương \(a,b\)thỏa mãn \(a+b=1.\)Ta có: \(\frac{1}{a+1}+\frac{1}{b+1}\ge \frac{4}{a+1+b+1}=\frac{4}{3}\)

Chọn A.

Phương pháp giải:

Xác định dấu của \(a\) và \(b\) từ đó chọn đáp án đúng.

Lời giải chi tiết:

Ta có \(\left\{ \begin{array}{l}a + b < a\\b - a > b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b < 0\\ - a > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b < 0\\a < 0\end{array} \right. \Leftrightarrow ab > 0\).

Chọn A.

Phương pháp giải:

Sử dụng hằng đẳng thức.

Lời giải chi tiết:

\({a^2} + {b^2} + ab < 0\,\,\forall a;b \in R\) là sai vì \({a^2} + ab + {b^2} = {a^2} + 2a\frac{1}{2}b + \frac{{{b^2}}}{4} + \frac{{3{b^2}}}{4} = {\left( {a + \frac{b}{2}} \right)^2} + \frac{{3{b^2}}}{4} \ge 0\).

Chọn: C

Phương pháp giải:

Tách hạng tử, áp dụng bất đẳng thức Cosi cho hai số không âm.

Lời giải:

Lời giải chi tiết:

Ta có \(f\left( x \right)=x+\frac{2}{x-1}=x-1+\frac{2}{x-1}+1\ge 2\sqrt{\left( x-1 \right).\frac{2}{x-1}}+1=2\sqrt{2}+1.\)

Dấu \(''\,\,=''\) xảy ra \(\Leftrightarrow \left\{ \begin{align}  x>1 \\  x-1=\frac{2}{x-1} \\ \end{align} \right.\Leftrightarrow x=1+\sqrt{2}.\) Vậy \(m=2\sqrt{2}+1.\)

Chọn B

Phương pháp giải:

\(\left\{ \begin{array}{l}a > b\\c > 0\end{array} \right. \Leftrightarrow ac > bc\).

Lời giải chi tiết:

Theo bài ra ta có \(a + 2c > b + 2c \Leftrightarrow a > b\).

\(a > b \Leftrightarrow 2a > 2b \Rightarrow \) Đáp án C đúng.

Chọn C.

Phương pháp giải:

\(\left\{ \begin{array}{l}
a < b\\
c > 0
\end{array} \right. \Leftrightarrow ac < bc;\,\,\left\{ \begin{array}{l}
a < b\\
c < 0
\end{array} \right. \Leftrightarrow ac > bc\)

Lời giải chi tiết:

Đáp án đúng là \(\left\{ \begin{array}{l}a < b\\c > 0\end{array} \right. \Leftrightarrow ac < bc\) do \(c > 0\) nên không làm thay đổi chiều bất đẳng thức.

Chọn D.

Phương pháp giải:

Suy luận, kết hợp sử dụng định nghĩa và tính chất của bất đẳng thức.

Lời giải chi tiết:

A. \(ac > bd\) chỉ đúng khi \(a > b > 0\) và \(c > d > 0\).

B. \(a - c > b - d\). Không có tính chất trừ vế với vế hai bất đẳng thức cùng dấu thì được một bất đẳng thức cùng dấu.

C. \(a - d > b - c\) đúng. Vì sử dụng tính chất cơ bản \(a > b;\,c > d \Rightarrow a + c > b + d\) kết hợp với biến đổi tương đương ta có: \(a - d > b - c\).

D. \( - ac >  - bd\) chỉ đúng khi \(0 > a > b\) và \(0 > c > d\)

Chọn C.

Phương pháp giải:

Thêm, bớt để xuất hiện các số dương.

Áp dụng bất đẳng thức Cauchy cho hai số dương \(x - 1\) và \({4 \over {x - 1}}\)

Lời giải chi tiết:

Ta có: \(f(x) = x - 1 + {4 \over {x - 1}} + 1\)

Trên \((1, + \infty )\) ta có hai số dương \(x - 1\) và \({4 \over {x - 1}}\).

Áp dụng bất đẳng thức Cauchy cho hai số dương ta có: \(\left( {x - 1} \right) + {4 \over {x - 1}} \ge 2\sqrt {\left( {x - 1} \right).{4 \over {x - 1}}}  = 4\).

Suy ra \(f\left( x \right) \ge 4 + 1 = 5\).

Chọn B.

Phương pháp giải:

Áp dụng BĐT  \(\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}\) và phương pháp ghép đối xứng.

Lời giải chi tiết:

Áp dụng BĐT  \(\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}\) ta có: \(\frac{1}{p-a}+\frac{1}{p-b}\ge \frac{4}{\left( p-a \right)+\left( p-b \right)}\Leftrightarrow \frac{1}{p-a}+\frac{1}{p-b}\ge \frac{4}{c}\,\,\,\,\,\,\,\,\,\,(1)\)

Tương tự:

\(\frac{1}{p-b}+\frac{1}{p-c}\ge \frac{4}{a}\,\,\,\,\,\,\,\,\,(2)\)                    

\(\frac{1}{p-c}+\frac{1}{p-a}\ge \frac{4}{b}\,\,\,\,\,\,\,\,\,(3)\)

\(\left( 1 \right)+\left( 2 \right)+\left( 3 \right)\Leftrightarrow 2\left( \frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c} \right)\ge 4\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\Leftrightarrow \frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c}\ge 2\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\)

Chọn D.

Phương pháp giải:

Áp dụng BĐT  \(\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}\) và phương pháp ghép đối xứng.

Lời giải chi tiết:

Với \(a,b,c\)là các số dương. Ta có : \(\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}\) ;  \(\frac{1}{b}+\frac{1}{c}\ge \frac{4}{b+c}\) ;  \(\frac{1}{c}+\frac{1}{a}\ge \frac{4}{c+a}\)

Cộng vế với vế ta được : \(2\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\ge \frac{4}{a+b}+\frac{4}{b+c}+\frac{4}{c+a}\)

Điều này tương đương với \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge 2\left( \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a} \right)\)

Chọn B.

Phương pháp giải:

Áp dụng các công thức tính diện tích: \(S=\frac{1}{2}a.{{h}_{a}}=\frac{1}{2}b.{{h}_{b}}=\frac{1}{2}c.{{h}_{c}}\) và \(S=p.r\)

Áp dụng bất đẳng thức \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge \frac{9}{a+b+c}\) với a, b, c là độ dài các cạnh

Lời giải chi tiết:

Áp dụng các công thức tính diện tích: \(S=\frac{1}{2}a.{{h}_{a}}=\frac{1}{2}b.{{h}_{b}}=\frac{1}{2}c.{{h}_{c}}\)ta có:

\({{h}_{a}}+{{h}_{b}}+{{h}_{c}}=\frac{2S}{a}+\frac{2S}{b}+\frac{2S}{c}=2S\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\)

Áp dụng bất đẳng thức \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge \frac{9}{a+b+c}\), suy ra : \({{h}_{a}}+{{h}_{b}}+{{h}_{c}}\ge 2S.\frac{9}{a+b+c}=2S.\frac{9}{2p}=\frac{9S}{p}\)

Áp dụng công thức \(S=p.r\), suy ra \({{h}_{a}}+{{h}_{b}}+{{h}_{c}}\ge 9r\)

Chọn A.

Phương pháp giải:

Để sử dụng được giả thiết a + b + c = 3, ta cần đánh giá làm mất từng dấu căn thức trong biểu thức S. Ta sử dụng bất đẳng thức \(\sqrt {ab}  \le {{a + b} \over 2}\) như sau: \(\sqrt {3a + b}  = {1 \over {\sqrt \alpha  }}\sqrt {\left( {3a + b} \right).\alpha }  = {1 \over {\sqrt \alpha  }}.{{3a + b + \alpha } \over 2}\).

Dấu \('' = ''\) xảy ra khi \(3a + b = \alpha \)

Tương tự với \(\sqrt {3b + c} \) và \(\sqrt {3c + a} \)

Vấn đề đặt ra là làm thế nào ta tìm được hệ số \(\alpha \) ?

Dựa vào giả thiết \(a + b + c = 3\) và nhận xét biểu thức S có tính chất đối xứng đối với các biến \(a,b,c\) nên ta dự đoán dấu = xảy ra khi \(a = b = c = 1\).

Suy ra \(3a + b = 4\). Do đó \(\alpha  = 4\).  

Lời giải chi tiết:

\(\sqrt {3a + b}  = {1 \over 2}.\sqrt {\left( {3a + b} \right).4}  \le {1 \over 2}.{{\left( {3a + b} \right) + 4} \over 2} = {1 \over 4}.(3a + b + 4)\)

Tương tự:  \(\sqrt {3b + c}  \le {1 \over 4}.(3b + c + 4)\) và \(\sqrt {3c + a}  \le {1 \over 4}.(3c + a + 4)\)

\( \Rightarrow S = \sqrt {3a + b}  + \sqrt {3b + c}  + \sqrt {3c + a}  \le {1 \over 4}\left[ {4\left( {a + b + c} \right) + 12} \right]\)

Vì a + b + c = 3 nên ta có \(S \le 6\)

\(\,Max\,S = 6 \Leftrightarrow \left\{ \matrix{  3a + b = 4  \cr   3b + c = 4 \hfill \cr   3c + a = 4  \cr   a + b + c = 3  \cr}  \right. \Leftrightarrow a = b = c = 1\)

Chọn C.

Phương pháp giải:

Sử dụng phương pháp tách \(\dfrac{{a + b}}{c} = \dfrac{a}{c} + \dfrac{b}{c}\) sau đó sử dụng BĐT Cô-si cho ba số \(x,y,z \ge 0:\,\,x + y + z \ge 3\sqrt[3]{{xyz}}\). Dấu "=" xảy ra \( \Leftrightarrow x = y = z\).

Lời giải chi tiết:

Ta có: \(f\left( x \right) = \dfrac{{2{x^3} + 4}}{x} = 2{x^2} + \dfrac{4}{x} = 2{x^2} + \dfrac{2}{x} + \dfrac{2}{x}\).

Do \(x > 0 \Rightarrow \) Áp dụng BĐT Cô-si cho 3 số dương \(2{x^2},\,\,\dfrac{2}{x},\,\,\dfrac{2}{x}\) ta có:

\(f\left( x \right) \ge 3\sqrt[3]{{2{x^2}.\dfrac{2}{x}.\dfrac{2}{x}}} = 3.2 = 6\).

Dấu "=" xảy ra \(2{x^2} = \dfrac{2}{x} \Leftrightarrow {x^3} = 1 \Leftrightarrow x = 1\) (tm).

\( \Rightarrow \min f\left( x \right) = 6 \Leftrightarrow x = 1\).

Vậy \(m = 6\).

Chọn C.

Phương pháp giải:

Áp dụng bất đẳng thức hệ quả của BĐT Cô-si : \(ab \le \dfrac{{{{\left( {a + b} \right)}^2}}}{4}\).

Lời giải chi tiết:

Ta có: \(f\left( x \right) = \left( {6x + 3} \right)\left( {5 - 2x} \right) = 3\left( {2x + 1} \right)\left( {5 - 2x} \right) \le 3.\dfrac{{{{\left( {2x + 1 + 5 - 2x} \right)}^2}}}{4} = 27\).

Dấu "=" xảy ra \( \Leftrightarrow 2x + 1 = 5 - 2x \Leftrightarrow 4x = 4 \Leftrightarrow x = 1\,\,\left( {tm} \right)\).

\( \Rightarrow f\left( x \right) \le 27 \Rightarrow \max f\left( x \right) = 27 \Leftrightarrow x = 1\).

Vậy \(M = 27\).

Chọn C.

Phương pháp giải:

Áp dụng bất đẳng thức Cô- si cho 3 số không âm \(a,b,c:\,\,\,\,a + b + c \ge 3\sqrt[3]{{abc}}\), dấu “=” xảy ra khi và chỉ khi \(a = b = c\).

Lời giải chi tiết:

Ta có: \(B = a{b^2} = \frac{1}{2}.\left( {2a.b.b} \right)\mathop  \le \limits^{Co\,si} \frac{1}{2}.{\left( {\frac{{2a + b + b}}{3}} \right)^3} = \frac{1}{2}.{\left( {\frac{{2.1}}{3}} \right)^3} = \frac{4}{{27}}\) (với \(a + b = 1\))

\( \Rightarrow \) Giá trị lớn nhất của B là \(\frac{4}{{27}}\)khi \(2a = b,\,\,a + b = 1 \Leftrightarrow a = \frac{1}{3},\,b = \frac{2}{3}\).

Chọn: C

Phương pháp giải:

Sử dụng bất đẳng thức với \(a,b\)là hai số dương ta có \(\frac{4}{a+b}\le \frac{1}{a}+\frac{1}{b}\) (*)

Lời giải chi tiết:

Ta có

\(4T=4\left( \frac{3}{a+b}+\frac{2}{b+c}+\frac{1}{c+a} \right)\text{ }=3\frac{4}{a+b}+2\frac{4}{b+c}+\frac{4}{c+a}\le \text{ }3\left( \frac{1}{a}+\frac{1}{b} \right)+2\left( \frac{1}{b}+\frac{1}{c} \right)+\left( \frac{1}{a}+\frac{1}{c} \right)=\frac{4}{a}+\frac{5}{b}+\frac{3}{c}\)

Suy ra \(T\le \frac{1}{a}+\frac{5}{4b}+\frac{3}{4c}.\)

Chọn C.

Phương pháp giải:

Với \(a,b\)là hai số dương ta có bất đẳng thức: \(\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}\) hay \(\frac{1}{a+b}\le \frac{1}{4}\left( \frac{1}{a}+\frac{1}{b} \right)\)(*)

Lời giải chi tiết:

Áp dụng bất đẳng thức (*) ta có: \(\frac{1}{2a+b+c}=\frac{1}{2a+\left( b+c \right)}\le \text{ }\frac{1}{4}\left( \frac{1}{2a}+\frac{1}{b+c} \right)=\frac{1}{8a}+\frac{1}{4}.\frac{1}{b+c}\) 

 Tiếp tục áp dụng bất đẳng thức (*) ta có: \(\frac{1}{b+c}\le \frac{1}{4}\left( \frac{1}{b}+\frac{1}{c} \right)\)

Từ đó, suy ra \(\frac{1}{2a+b+c}\le \frac{1}{8a}+\frac{1}{16}\left( \frac{1}{b}+\frac{1}{c} \right)\)

Tương tự ta có: \(\frac{1}{a+2b+c}\le \frac{1}{8b}+\frac{1}{16}\left( \frac{1}{a}+\frac{1}{c} \right);\,\,\frac{1}{a+b+2c}\le \frac{1}{8c}+\frac{1}{16}\left( \frac{1}{b}+\frac{1}{a} \right)\)

Cộng vế với vế ta có \(P=\frac{1}{2a+b+c}+\frac{1}{a+2b+c}+\frac{1}{a+b+2c}\le \frac{1}{4}\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\)

Theo giả thiết \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=4\) nên ta có \(P\le 1\).

Chọn A.

Phương pháp giải:

Biến đổi biểu thức để khi áp dụng BĐT Cô-si triệt tiêu hết \(x\)

Lời giải chi tiết:

Ta có: \(f\left( x \right) = \frac{4}{x} + \frac{x}{{1 - x}} - 1 = \frac{{4 - x}}{x} + \frac{x}{{1 - x}} = \frac{{4 - 4x + 3x}}{x} + \frac{x}{{1 - x}} = \frac{{4\left( {1 - x} \right)}}{x} + \frac{x}{{1 - x}} + 3\)

Vì  \(0 < x < 1 \Rightarrow \frac{{1 - x}}{x} > 0;\,\,\,\,\frac{x}{{1 - x}} > 0\)

Áp dụng BĐT Cô-si ta được: \(f\left( x \right) \ge 2\sqrt 4  + 3 = 7\)

Dấu “=” xảy ra \( \Leftrightarrow \frac{{x - 1}}{x} = \frac{x}{{x - 1}} \Leftrightarrow {\left( {x - 1} \right)^2} = {x^2} \Leftrightarrow x = \frac{1}{2}\,\,\,\left( {tm} \right).\)

Vậy \(\mathop {Min}\limits_{\left( {0;\,\,1} \right)} \,\,f\left( x \right) = 7\,\,\,\,khi\,\,\,\,x = \frac{1}{2}.\)

Chọn B.

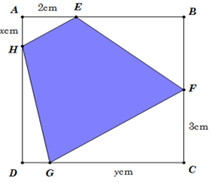
Phương pháp giải:

- Sử dụng phương pháp phần bù: \({S_{EFGH}}\) nhỏ nhất \( \Leftrightarrow S = {S_{\Delta AEH}} + {S_{\Delta CGF}} + {S_{\Delta DGH}}\) lớn nhất.

- Lập biểu thức tính \(S\) theo \(x,y\) rồi đánh giá GTLN của \(S\).

Lời giải chi tiết:

Ta có \({S_{EFGH}} = {S_{ABCD}} - {S_{AEH}} - {S_{BEF}} - {S_{CFG}} - {S_{DGH}}\)

Mà \({S_{ABCD}} = 6.6 = 36;{S_{BEF}} = \dfrac{1}{2}BE.BF = \dfrac{1}{2}.4.3 = 6\) nên \({S_{EFGH}} = 30 - \left( {{S_{\Delta AEH}} + {S_{\Delta CGF}} + {S_{\Delta DGH}}} \right)\)

Do đó \({S_{EFGH}}\) nhỏ nhất \( \Leftrightarrow S = {S_{\Delta AEH}} + {S_{\Delta CGF}} + {S_{\Delta DGH}}\) lớn nhất.

Ta có: \(S = \dfrac{1}{2}AE.AH + \dfrac{1}{2}CF.CG + \dfrac{1}{2}DG.DH\)     \( = x + \dfrac{{3y}}{2} + \dfrac{{\left( {6 - x} \right)\left( {6 - y} \right)}}{2}\)

\( \Rightarrow 2S = 2x + 3y + \left( {6 - x} \right)\left( {6 - y} \right)\) \( = xy - 4x - 3y + 36\) \(\left( 1 \right)\)

Ta có \(EFGH\) là hình thang \( \to \) \(\widehat {AEH} = \widehat {CGF}\)

\( \Rightarrow \Delta AEH~\Delta CGF\)\( \Rightarrow \dfrac{{AE}}{{CG}} = \dfrac{{AH}}{{CF}}\) \( \Rightarrow \dfrac{2}{y} = \dfrac{x}{3} \Rightarrow xy = 6\) \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(2S = 42 - \left( {4x + \dfrac{{18}}{x}} \right)\).

Để \(2S\) lớn nhất khi và chỉ khi \(4x + \dfrac{{18}}{x}\) nhỏ nhất.

Mà \(4x + \dfrac{{18}}{x} \ge 2\sqrt {4x.\dfrac{{18}}{x}}  = 12\sqrt 2 .\)

Dấu \('' = ''\) xảy ra \( \Leftrightarrow 4x = \dfrac{{18}}{x} \Leftrightarrow x = \dfrac{{3\sqrt 2 }}{2} \to y = 2\sqrt 2 \).

Chọn  C.

Phương pháp giải:

Lời giải chi tiết:

Ta có \(\frac{1}{x}+\frac{1}{y}\ge \frac{4}{x+y}\)

Do đó \(A\ge (x+y)+\frac{4}{x+y}\) (1)

Ta có \(\left( x+y \right)+\frac{4}{x+y}=\left( x+y \right)+\frac{1}{x+y}+\frac{3}{x+y}\)

Áp dụng bất đẳng thức Cauchy cho hai số dương ta có \(\left( x+y \right)+\frac{1}{x+y}\ge 2\)

Mặt khác, do \(x+y\le 1\)nên ta có \(\frac{3}{x+y}\ge 3\)

Suy ra \(\left( x+y \right)+\frac{4}{x+y}\ge 5\) (2)

Từ (1) và (2) có \(A\ge 5\)

Dấu “=” xảy ra khi và chỉ khi x + y = 1.

Chọn B.

Phương pháp giải:

Biến đổi tương đương.

Lời giải chi tiết:

Ta có:

\(\eqalign{  & P = {a^3} + {b^3} + {c^3} - 3abc = {\left( {a + b + c} \right)^3} - 3\left( {a + b + c} \right)\left( {ab + bc + ca} \right)  \cr   &  = \left( {a + b + c} \right)\left[ {{{\left( {a + b + c} \right)}^2} - 3\left( {ab + bc + ca} \right)} \right]  \cr   &  = \left( {a + b + c} \right)\left[ {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right] \cr} \)

Ta có:

\(\eqalign{  & {a^2} + {b^2} + {c^2} - ab - bc - ca = {1 \over 2}\left[ {\left( {{a^2} - 2ab + {b^2}} \right) + \left( {{b^2} - 2bc + {c^2}} \right) + \left( {{c^2} - 2ca + {a^2}} \right)} \right]  \cr   &  = {1 \over 2}\left[ {{{\left( {a - b} \right)}^2} + {{\left( {b - c} \right)}^2} + {{\left( {c - a} \right)}^2}} \right] > 0 \cr} \)

(vì \(a,b,c\) đôi một khác nhau)

Mặt khác theo giả thiết \(a + b + c < 0\). Do đó \(P < 0\)

Chọn B.

Phương pháp giải:

Áp dụng công thức \(\cos \left( {\alpha  \pm \beta } \right) = \cos \alpha \cos \beta  \mp \sin \alpha \sin \beta \) để tìm giá trị nhỏ nhất của \(3a + 4b\) từ đó tìm giá trị lớn nhất của \(P\)

Lời giải chi tiết:

Ta có: \({a^2} + {b^2} = 2 \Rightarrow {\left( {\frac{a}{{\sqrt 2 }}} \right)^2} + {\left( {\frac{b}{{\sqrt 2 }}} \right)^2} = 1 \Rightarrow \) Gọi \(\alpha \) là góc có \(\sin \alpha  = \frac{a}{{\sqrt 2 }};\cos \alpha  = \frac{b}{{\sqrt 2 }}\)

Lại có: \({\left( {\frac{3}{5}} \right)^2} + {\left( {\frac{4}{5}} \right)^2} = 1 \Rightarrow \) Gọi \(\beta \) là góc có \(\sin \beta  = \frac{3}{5};\cos \beta  = \frac{4}{5}\)

\(\begin{array}{l} \Rightarrow \frac{a}{{\sqrt 2 }}.\frac{3}{5} + \frac{b}{{\sqrt 2 }}.\frac{4}{5} = \sin \alpha \sin \beta  + \cos \alpha \cos \beta  = \cos \left( {\alpha  - \beta } \right) \ge  - 1\\ \Rightarrow 3a + 4b \ge  - 5\sqrt 2 .\end{array}\) 

Ta có: \({c^2} + {d^2} + 25 = 6c + 8d \Leftrightarrow \left( {{c^2} - 6c + 9} \right) + \left( {{d^2} - 8d + 16} \right) = 0 \Leftrightarrow {\left( {c - 3} \right)^2} + {\left( {d - 4} \right)^2} = 0\,\,\left( * \right)\)

Mà \(\left\{ \begin{array}{l}{\left( {c - 3} \right)^2} \ge 0\,\,\,\,\,\forall c\\{\left( {d - 4} \right)^2} \ge 0\,\,\,\,\,\forall d\end{array} \right. \Rightarrow \left( * \right) \Leftrightarrow c - 3 = d - 4 = 0 \Rightarrow \left\{ \begin{array}{l}c = 3\\d = 4\end{array} \right.\)

Khi đó \(P = 9 + 16 - \left( {3a + 4b} \right) = 25 - \left( {3a + 4b} \right) \le 25 - \left( { - 5\sqrt 2 } \right) = 25 + 5\sqrt 2 \)

Chọn B.

Phương pháp giải:

+) Tìm ĐKXĐ của hàm số.

+) Sử dụng phương pháp bình phương 2 vế.

+) Đánh giá, sử dụng BĐT Cô-si, chứng minh \(m \le f\left( x \right) \le M\).

Lời giải chi tiết:

ĐKXĐ: \(\left\{ \begin{array}{l}x - 4 \ge 0\\8 - x \ge 0\end{array} \right. \Leftrightarrow 4 \le x \le 8\).

+) Ta có \({f^2}\left( x \right) = 4\left( {x - 4} \right) + 8 - x + 4\sqrt {\left( {x - 4} \right)\left( {8 - x} \right)}  = 3x - 8 + 4\sqrt {\left( {x - 4} \right)\left( {8 - x} \right)} \).

         \( \Leftrightarrow {f^2}\left( x \right) = 3\left( {x - 4} \right) + 4\sqrt {\left( {x - 4} \right)\left( {8 - x} \right)}  + 4\).

    Ta có \(\left\{ \begin{array}{l}x - 4 \ge 0\\\sqrt {\left( {x - 4} \right)\left( {8 - x} \right)}  \ge 0\end{array} \right. \Leftrightarrow {f^2}\left( x \right) \ge 4 \Leftrightarrow f\left( x \right) \ge 2\)

    Dấu "=" xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x - 4 = 0\\\left( {x - 4} \right)\left( {8 - x} \right) = 0\end{array} \right. \Leftrightarrow x = 4\). Vậy \(m = 2\).

+) Với \(x \in \left[ {4;8} \right]\), áp dụng BĐT Cô-si ta có:

    \(\begin{array}{l}x - \dfrac{4}{5} = x - 4 + \dfrac{{16}}{5} \ge 2\sqrt {\left( {x - 4} \right).\dfrac{{16}}{5}}  = \dfrac{{8\sqrt {x - 4} }}{{\sqrt 5 }}\,\,\,\,\left( 1 \right)\\\dfrac{{44}}{5} - x = 8 - x + \dfrac{4}{5} \ge 2\sqrt {\left( {8 - x} \right)\dfrac{4}{x}}  = \dfrac{{4\sqrt {8 - x} }}{{\sqrt 5 }}\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)

Cộng vế (1) với (2) ta có: \(\dfrac{{8\sqrt {x - 4}  + 4\sqrt {8 - x} }}{{\sqrt 5 }} \le x - \dfrac{4}{5} + \dfrac{{44}}{5} - x = 8\).

\( \Rightarrow \pi 8\sqrt {x - 4}  + 4\sqrt {8 - x\sqrt 5 }  \le 8 \Leftrightarrow \dfrac{{4f\left( x \right)}}{{\sqrt 5 }} \le 8 \Leftrightarrow f\left( x \right) \le 2\sqrt 5 \).

Dấu "=" xảy ra \( \Leftrightarrow x = \dfrac{{36}}{5}\). Vậy \(M = 2\sqrt 5 \).

Chọn C.