50 bài tập Ôn tập chương 2: Sóng cơ và sóng âm (Phần 1)Làm bàiCâu hỏi 1 : Chọn phát biểu SAIkhi nói về môi trường truyền âm và vận tốc âm:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Câu hỏi 2 : Khi sóng âm truyền từ môi trường không khí vào môi trường nước thì
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B + Khi sóng cơ lan truyền qua các môi trường thì tần số của nó là không đổi. Câu hỏi 3 : Khi nói về sóng cơ, phát biểu nào sau đây sai?
Đáp án: C Phương pháp giải: Môi trường truyền sóng của sóng cơ Lời giải chi tiết: Đáp án D + Sóng cơ lan truyền được trong môi trường rắn, lỏng và khí tuy nhiên không lan truyền được trong chân không Câu hỏi 4 : Cho các chất sau: không khí ở 00C, không khí ở 250C, nước và sắt. Sóng âm truyền chậm nhất trong
Đáp án: D Phương pháp giải: Sử dụng kiến thức về tốc độ truyền âm Lời giải chi tiết: Tốc độ truyền âm trong không khí ở 00C là 331m/s; ở không khí 250C là 346m/s; ở nước là 1500 m/s và ở sắt là 5850 m/s. Vậy âm truyền chậm nhất trong không khí ở 00C Câu hỏi 5 : Chọn phát biểu sai khi nói về sóng âm.
Đáp án: C Phương pháp giải: Độ to của âm là một đặc trưng sinh lý gắn liền với mức cường độ âm. Mức cường độ âm được đo bằng đơn vị Ben, đề xi Ben. Lời giải chi tiết: Độ to của âm là một đặc trưng sinh lý gắn liền với mức cường độ âm. Mức cường độ âm được đo bằng đơn vị Ben, đề xi Ben. Câu hỏi 6 : Một lá thép mỏng, một đầu cố định, đầu còn lại được kích thích để dao động với chu kì không đổi và bằng 0,008 s, cường độ âm đủ lớn. Âm do lá thép phát ra là
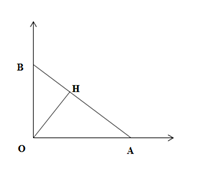
Đáp án: C Phương pháp giải: Âm nghe được có tần số nằm trong khoảng 16Hz đến 20000Hz Lời giải chi tiết: T = 0,08s Tần số âm: f = 1/T = 125Hz là âm nghe được Câu hỏi 7 : Trên mặt thoáng của một chất lỏng, một mũi nhọn O chạm vào mặt thoáng dao động điều hòa với tần số f tạo thành sóng trên mặt thoáng với bước sóng λ. Xét trên hai phương truyền sóng Ox và Oy vuông góc với nhau. Gọi A là điểm thuộc Ox cách O một đoạn 16λ và B thuộc Oy cách O là 12λ. Tìm số điểm dao động ngược pha với nguồn trên đoạn AB
Đáp án: A Phương pháp giải: Tại M ngược pha với nguồn thì d = kλ với k là số bán nguyên Lời giải chi tiết: OA = 16λ; OB = 12λ nên AB = 20λ M ngược pha với nguồn nên d = kλ với k là số bán nguyên Đường cao OH=OA.OBAB=9,6λ + Xét điểm M nằm trong đoạn AH ngược pha với nguồn: OH≤d≤OA⇒k=10,5;11,5;12,5;13,5;14,5;15,5 Vậy có 6 giá trị k + Xét điểm M nằm trong đoạn BH ngược pha với nguồn: OH≤d≤OB⇒10≤k≤12⇒k=10,5;11,5 Vậy có 2 giá trị k Như vậy tổng hợp trên AB có 8 giá trị k Câu hỏi 8 : Cho các kết luận sau về sóng âm (1) Sóng âm có tần số từ 16 Hz đến 20000 Hz gọi là âm nghe được (âm thanh) (2)Trong mỗi môi trường đồng tính, âm truyền với tốc độ xác định. Sóng âm truyền lần lượt trong các môi trường rắn, lỏng, khí với tốc độ tăng dần. Sóng âm không truyền được trong chân không. (3) Tần số, cường độ âm, mức cường độ âm, đồ thị dao động là các đặt trưng vật lí của âm. Độ cao, độ to, âm sắc là đặc trưng sinh lý của âm. (4) Độ cao của âm gắn liền với tần số âm; độ to của âm gắn liền với mức cường độ âm; âm sắc có liên quan mật thiết với đồ thị dao động âm. (5) Tần số dao động của nguồn âm cũng là tần số của sóng âm. Sóng âm không mang theo năng lượng. Số kết luận đúng là
Đáp án: A Phương pháp giải: Sử dụng lí thuyết về sóng âm Lời giải chi tiết: Các phát biểu đúng là (1) Sóng âm có tần số từ 16 Hz đến 20000 Hz gọi là âm nghe được (âm thanh) (3) Tần số, cường độ âm, mức cường độ âm, đồ thị dao động là các đặt trưng vật lí của âm. Độ cao, độ to, âm sắc là đặc trưng sinh lý của âm. (4) Độ cao của âm gắn liền với tần số âm; độ to của âm gắn liền với mức cường độ âm; âm sắc có liên quan mật thiết với đồ thị dao động âm. Như vậy số phát biểu đúng là 3 Chọn đáp án A Câu hỏi 9 : Chọn ý sai? Hộp đàn có tác dụng
Đáp án: A Phương pháp giải: Hộp đàn không làm thay đổi tần số của âm Độ cao của âm phụ thuộc vào tần số âm Lời giải chi tiết: Hộp đàn không làm thay đổi tần số của âm nên nói hộp đàn làm âm phát ra cao hơn là sai. Chọn A Câu hỏi 10 : Khi mộ sóng âm truyền từ nước ra không khí thì
Đáp án: B Phương pháp giải: Khi sóng âm truyền qua các môi trường khác nhau thì tần số sóng không đổi Lời giải chi tiết: Khi sóng âm truyền từ nước ra không khí thì tần số của sóng là không đổi, vận tốc truyền sóng giảm nên bước sóng sẽ giảm. Đáp án B Câu hỏi 11 : Để tăng gấp đôi tần số của âm do một dây đàn phát ra, ta phải
Đáp án: B Phương pháp giải: Tần số sóng liên hệ với lực căng dây: f=vλ=1λ√Fm Lời giải chi tiết: Tần số sóng liên hệ với lực căng dây: f=vλ=1λ√Fm Vậy để tăng tần số 2 lần thì lực căng dây phải tăng 4 lần Chọn B Câu hỏi 12 : Để đo độ sâu vực sâu nhất thế giới Mariana ở Thái Bình Dương, người ta dùng phương pháp định vị hồi âm bằng sóng siêu âm. Sau khi phát ra siêu âm hướng xuống biển thì sau 14,53s người ta mới nhận được tín hiệu phản xạ của nó từ đáy biển. Vận tốc truyền của siêu âm trong nước biển là 1500m/s, trong không khí là 340m/s. Độ sâu vực Mariana là
Đáp án: D Phương pháp giải: Quãng đường sóng siêu âm đi được cho tới khi thu được tín hiệu bằng 2 lần độ sâu của rãnh Quãng đường đi được trong chuyển đông thẳng đều: s = vt Lời giải chi tiết: Quãng đường sóng siêu âm đi được cho tới khi thu được tín hiệu bằng 2 lần độ sâu của rãnh 2d = vt = 1500.14,53 => d = 10897,5m Chọn D Câu hỏi 13 : Đặc điểm nào sau đây không phải của sóng cơ?
Đáp án: B Phương pháp giải: Vận tốc truyền sóng cơ trong chất rắn lớn hơn trong chất lỏng, và lớn hơn trong chất khí.. Lời giải chi tiết: Vận tốc truyền sóng cơ trong chất rắn lớn hơn trong chất lỏng, và lớn hơn trong chất khí.. Chọn B Câu hỏi 14 : Tiến hành thí nghiệm đo tốc độ truyền âm trong không khí, một học sinh đo được bước sóng của sóng âm là 75 ± 1 cm, tần số dao động của âm thoa là 440 ± 10 Hz. Tốc độ truyền âm tại nơi làm thí nghiệm là
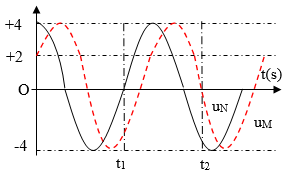
Đáp án: C Phương pháp giải: Áp dụng công thức tính tốc độ truyền sóng âm: v=λ.f Công thức tính sai số tuyệt đối của phép đo : Δv=(Δλˉλ+Δfˉf).ˉv Lời giải chi tiết: Tốc độ truyền sóng âm: v=λ.f⇒ˉv=ˉλ.ˉf=0,75.440=330(m/s) Sai số tuyệt đối của phép đo: Δv=(Δλˉλ+Δfˉf).ˉv=(0,010,75+10440).330=11,9(m/s) Tốc độ truyền âm tại nơi làm thí nghiệm là: 330,0 ± 11,9 m/s. Chọn C Câu hỏi 15 : Sóng ngang có tần số f truyền trên một sợi dây đàn hồi rất dài, với tốc độ 4,5m/s. Xét hai điểm M và N trên cùng một phương truyền sóng, cách nhau một khoảng x nhỏ hơn một bước sóng, sóng truyền từ N đến M. Đồ thị biểu diễn li độ sóng của M và N cùng theo thời gian như hình vẽ. Biết t1=0,05s. Tại t2, khoảng cách giữa phần tử chất lỏng tại M và N có giá trị gần giá trị nào nhất sau đây?
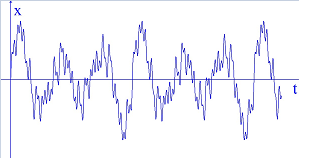
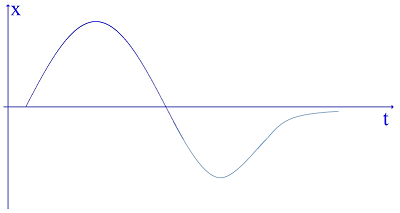
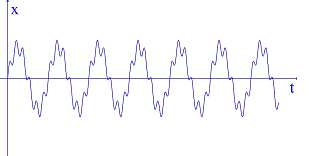
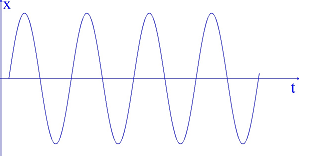
Đáp án: B Phương pháp giải: Lời giải chi tiết: Từ đồ thị ta thấy N sớm pha hơn M một góc π3; 2πMNλ=π3→MN=λ6; xác định được T4+T2=0,05s→T=115s→λ=v.T=30cm→MN=5cm; uM=4cos(ωt−π3)cm; uN=4cosωtcm; với t2=t1+T2+T6ta xác định được |uM−uN|t=t2=2√3cm→MNt=t2=√52+22.3=√37=6,082cm Chọn B Câu hỏi 16 : Trong thí nghiệm khảo sát đồ thị dao động của âm, đồ thị nào sau đây mô tả sự phụ thuộc của li độ x theo thời gian t của một âm do âm thoa phát ra?
Đáp án: D Phương pháp giải: Âm do âm thoa phát ra có một tần số xác định nên đồ thị dao động âm có dạng hình sin Lời giải chi tiết: Âm do âm thoa phát ra có một tần số xác định nên đồ thị dao động âm có dạng hình sin Chọn D Câu hỏi 17 : Trong giờ thực hành hiện tượng sóng dừng trên dây, một học sinh thực hiện như sau: tăng dần tần số của máy phát dao động thì thấy rằng khi sóng dừng xuất hiện trên dây tương ứng với 1 bó sóng và 9 bó sóng thì tần số thu được thỏa mãn f9−f1=200(Hz). Khi trên dây xuất hiện sóng dừng với 6 nút sóng thì máy phát tần số hiện giá trị là
Đáp án: B Phương pháp giải: Điều kiện để có sóng dừng khi 2 đầu là nút: ℓ=kλ2=k.v2fk Lời giải chi tiết: Từ điều kiện để có sóng dừng 2 đầu là nút, ta có: ℓ=1.v2f1=9v2f9=8v2(f9−f1)→f1=25(Hz); ℓ=1.v2f1=(6−1)v2f6→f6=5f1=125(Hz) Chọn B Câu hỏi 18 : Hình dưới đây mô tả một sóng dừng trên sợi dây MN. Gọi H là một điểm trên dây nằm giữa nút M và nút P, K là một điểm nằm giữa nút Q và nút N. Kết luận nào sau đây là đúng?
Đáp án: A Phương pháp giải: Sử dụng lý thuyết về pha dao động của các điểm trên sóng dừng. Lời giải chi tiết: Nhận xét: Hai điểm trên hai bó sóng liên tiếp thì ngược pha nhau. Giữa hai điểm H và K có 3 bó sóng, vậy hai điểm H và K dao động cùng pha với nhau. Chọn A. Câu hỏi 19 : Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, A là một điểm nút, B là một điểm bụng gần A nhất, C là trung điểm của AB, với AB = 10 cm. Biết khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại B bằng biên độ đao động của phần tử tại C là 0,2 s. Tốc độ truyền sóng trên dây là
Đáp án: B Phương pháp giải: Phương trình li độ của một điểm cách nút một khoảng x là: u=2A.sin(2πxλ).cos(ωt+π2)(cm) với AB=λ4=10cm⇒λ=4.10=40cm Tại C thì x=λ8=5cm từ đó tìm biên độ của C. Sử dụng giản đồ vecto quay để tìm chu kì T. Áp dụng công thức tính vận tốc truyền sóng v=λT Lời giải chi tiết: Phương trình li độ của một điểm cách nút một khoảng x là: u=2A.sin(2πxλ).cos(ωt+π2)(cm) với AB=λ4=10cm⇒λ=4.10=40cm Tại C thì x=λ8=5cm → Biên độ của C là : AC=2.A.sin(2π.λ8λ)=A.√2 Biên độ của B là 2A. Ta có giản đồ vecto quay như sau:
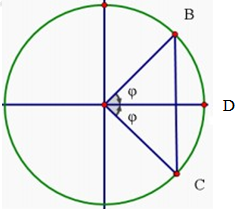
Ta có độ lớn góc α là α=arcosA√22A=450 Vậy thời gian liên tiếp hai lần liên tiếp B có li độ bằng biên độ của C là : t=2.4503600.T=T4 Vậy chu kì dao động là : T=4.t=4.0,2=0,8s Vận tốc truyền sóng là : v=λT=400,8=50(cm/s) Chọn B. Câu hỏi 20 : Một sóng cơ làn truyền trên một sợi dây dài. Ở thời điểm t0, tốc độ dao động của các phần tử tại B và C đều bằng v0, còn phần tử tại trung điểm D của BC đang ở vị trí biên. Ở thời điểm t1, vận tốc của các phần tử tại B và C đều có giá trị bằng v0 thì phần tử D lúc đó có tốc độ bằng
Đáp án: D Phương pháp giải: + Sử dụng vòng tròn lượng giác xác định vị trí của các điểm + Sử dụng hệ thức trên vòng tròn lượng giác. Lời giải chi tiết: Ta có: + Ở thời điểm t0, tốc độ dao động của các phần tử tại B và C đều bằng v0, còn phần tử tại trung điểm BC đang ở biên, biểu diễn trên vòng tròn lượng giác ta được + Ở thời điểm t1, vận tốc của các phần tử tại B và C có giá trị đều bằng v0 và biểu diễn trên vòng tròn lượng giác ta có Từ vòng tròn lượng giác tại hai thời điểm t0 và t1 ta có ^COB=const và vận tốc tại t0 và t1 bằng nhau nên φ=φ1=π4 Tại t1 vận tốc tại D đạt giá trị cực đại nên {cosφ=v1vmax=v0vmaxsinφ=v2vmax=v0vmax⇒vmax=√2v0 Chọn D Câu hỏi 21 : Tốc độ truyền âm của một âm trong không khí và trong nước lần lượt là 330 m/s và 1450 m/s. Khi âm truyền từ trong không khí vào trong nước thì bước sóng của nó tăng lên bao nhiều lần?
Đáp án: D Phương pháp giải: Công thức tính bước sóng : λ=v.T=vf Khi sóng truyền từ môi trường này sang môi trường khác thì tần số không đổi, vận tốc thay đổi. Lời giải chi tiết: Công thức tính bước sóng : λ=v.T=vf Khi sóng truyền từ môi trường này sang môi trường khác thì tần số không đổi, vận tốc thay đổi. Do đó khi sóng truyền từ không khí vào nước thì bước sóng của nó tăng lên số lần là : λ′λ=v′v=1450330≈4,4 Chọn D. Câu hỏi 22 : Để đo tốc độ âm trong gang, nhà vật lí Pháp Bi–ô đã dùng một ống gang dài 951,25 m. Một người đập một nhát búa vào một đầu ống gang, một người ở đầu kia nghe thấy hai tiếng gõ, một tiếng truyền qua gang và một truyền qua không khí trong ống gang, hai tiếng ấy cách nhau 2,5 s. Biết tốc độ âm trong không khí là 340 m/s. Tốc độ âm trong gang là bao nhiêu
Đáp án: B Phương pháp giải: Thời gian âm truyền trong môi trường: t=lv Lời giải chi tiết: Hai tiếng gõ cách nhau 2,5 s, ta có: lvkk−lvgang=2,5⇒951,25340−951,25vgang=2,5⇒vgang=3194(m/s) Chọn B. Câu hỏi 23 : Tai người không thể phân biệt được hai âm giống nhau nếu chúng tới tai chênh nhau về thời gian một lượng nhỏ hơn hoặc bằng 0,1 s. Một người đứng cách một bức tường một khoảng L bắn một phát súng. Cho biết tốc độ truyền âm trong không khí là 340 m/s. Người ấy chỉ nghe thấy một tiếng nổ khi L thỏa mãn điều kiện nào dưới đây?
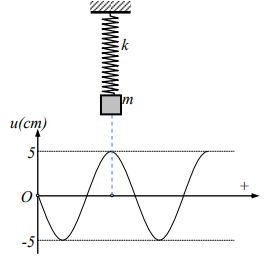
Đáp án: B Phương pháp giải: Thời gian truyền âm: t=sv Lời giải chi tiết: Quãng đường âm truyền đi rồi phản xạ trở lại là: s = 2L Thời gian âm truyền đi rồi phản xạ trở lại là: t=sv=2Lv Để không nghe được tiếng nổ, ta có: t≤0,1⇒2Lv≤0,1⇒L≤0,1v2=0,1.3402=17(m) Chọn B. Câu hỏi 24 : Một sợi dây đàn hồi rất dài được căng ngang và một con lắc lò xo treo trong cùng một mặt phẳng thẳng đứng. Con lắc lò xo có độ cứng k =10 N/m, vật nhỏ có khối lượng m = 25g dao động theo phương thẳng đứng. Khi vật cân bằng và sợi dây chưa có sóng truyền, vật cách sợi dây một đoạn bằng 5cm. Đầu O của dây được gắn với nguồn dao động điều hòa theo phương thẳng đứng tạo ra sóng ngang lan truyền trên dây với tần số góc w = 20 rad/s. Tại thời điểm t = 0, sợi dây có dạng như hình vẽ, còn vật nhỏ được giữ ở vị trí lò xo nén 2,5 cm. Tại thời điểm t =∆t, thả nhẹ để vật dao động tự do. Vật không chạm vào sợi dây trong quá trình dao động nếu ∆t nhận giá trị
Đáp án: A Phương pháp giải: Viết phương trình dao động, tìm điều kiện khoảng cách Lời giải chi tiết: Chọn trục Ox trùng với trục của lò xo, điểm O trùng với vị trí cân bằng của sợi dây. Ta viết được phương trình dao động của sợi dây là: u=U0.cos(20t)=5cos20t Tại thời điểm ∆t thì phương trình dao động của sợi dây là: u=5.cos(20t+20Δt)cm Tần số góc của con lắc lò xo là: ω=√km=√100,025=20rad/s Độ giãn của lò xo ở vị trí cân bằng là: m.g=k.Δl⇒Δl=mgk=0,025m=2,5cm Ban đầu lò xo bị nén 2,5cm, vậy biên độ dao động của lò xo là 5cm. Phương trình dao động của con lắc lò xo là: x=5cos(20t)+5 Vậy khoảng cách giữa vật nặng và sợi dây là: Δd=x−u=5+5cos20t−5cos(20t−20Δt)=5+A.cos(20t+φ) Với : A=√52+52−2.5.5.cosφ Điều kiện để vật dao động và sợi dây không chạm nhau là ∆d > 0 ⇒5−A>0⇒A<5⇒cosφ>12⇔cos20t>12 Dùng phép thử các đáp án, ta chọn đáp án A Câu hỏi 25 : Trong các kết luận sau, tìm kết luận sai:
Đáp án: D Phương pháp giải: + Nhạc âm là những âm có tần số xác định. Tạp âm là những âm không có tần số xác định. + Độ cao là một đặc tính sinh lí của âm gắn liền với tần số âm. + Độ to là một đặc trưng sinh lí của phụ thuộc vào mức cường độ âm và tần số âm. + Âm sắc là một đặc trưng sinh lí của âm, giúp ta phân biệt được âm do các nguồn khác nhau phát ra. Âm sắc có liên quan mật thiết với đồ thị dao động âm (tần số và biên độ). Lời giải chi tiết: Độ cao là một đặc tính sinh lí của âm gắn liền với tần số âm → Phát biểu sai là: Độ cao là một đặc tính sinh lí của âm phụ thuộc vào các đặc tính vật lí là tần số và năng lượng âm. Chọn D. Câu hỏi 26 : Một máy phát âm được dùng để gọi cá có thể phát ra âm trong nước có bước sóng là 6,8 cm. Biết vận tốc của sóng này trong nước là 1480 m/s. Âm do máy này phát ra là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Tần số của âm
siêu âm Câu hỏi 27 : Trong thí nghiệm đo tốc độ truyền âm trong không khí, một học sinh đo được bước sóng của sóng âm là (82,5±1,0) (cm), tần số dao động của âm thoa là (400 ± 10) ( Hz). Tốc độ truyền âm trong không khí tại nơi làm thí nghiệm là
Đáp án: C Phương pháp giải: áp dụng phương pháp tính sai số Lời giải chi tiết: ta có f=400±10Hzλ=82,5±1,0cmv=λ.f=>¯v=¯λ.¯f=82,5.400=33000cm/s=330m/s δv=δλ+δf ⇒Δvv=Δff+Δλλ=182,5+10400=0,037=>Δv=0,037.330=12m/s=>v=330±12m/s Câu hỏi 28 : Tốc độ truyền âm có giá trị lớn nhất trong môi trường nào sau đây?
Đáp án: A Phương pháp giải: Tốc độ truyền âm trong các môi trường: vR>vL>vK Lời giải chi tiết: Tốc độ truyền âm có giá trị lớn nhất trong nhôm. Chọn A. Câu hỏi 29 : Tiến hành thí nghiệm đo tốc độ truyền âm trong không khí. Một học sinh đo được bước sóng của sóng âm là 75 ±1 cm , tần số dao động của âm là 440 ± 10 Hz . Sai số của phép đo tốc độ truyền âm là
Đáp án: C Phương pháp giải: Phương pháp tính sai số và giá trị trung bình Lời giải chi tiết: Đáp án C Theo bài ra ta có ¯v=λf=75.440=33000cm/s=330m/sΔv=¯v(Δff+Δλλ)=330(10440+175)=11,9cm/s Câu hỏi 30 : Một nguồn âm điểm truyền sóng âm đẳng hướng vào trong không khí với tốc độ truyền âm là v. Khoảng cách giữa hai điểm gần nhau nhất trên cùng hướng truyền sóng âm dao động ngược pha nhau là d. Tần số của âm là
Đáp án: B Phương pháp giải: Độ lệch pha giữa hai điểm cách nhau khoảng d: φ=2πdλ Tần số âm: f=vλ Lời giải chi tiết: Hai điểm gần nhau nhất dao động ngược pha có: φ=π⇒π=2πdλ⇒λ=2d Tần số của âm là: f=vλ=v2d Chọn B. Câu hỏi 31 : Tại O có một nguồn phát sóng cơ với tần số f = 20 Hz, tốc độ truyền sóng là 60 cm/s. Ba điểm thẳng hàng A, B, C nằm trên cùng phương truyền sóng và cùng phía so với O. Biết OA = 8 cm; OB = 25,5 cm; OC = 40,5 cm. Số điểm dao động cùng pha với A trên đoạn BC là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Chọn B + Bước sóng của sóng λ=vf=3cm. Để điểm M là một điểm nằm giữa BC cùng pha với A thì dM−dA=kλ→dM=8+3kcm. + Với khoảng giá trị của dM:25,5cm≤dM≤40,5cm, kết hợp với chức năng Shift → Solve của casio ta tìm được 5 vị trí cùng pha. Câu hỏi 32 : Tiến hành thí nghiệm đo tốc độ truyền âm trong không khí, một học sinh đo được bước sóng của sóng âm là (75 ± 1) (cm), tần số dao động của âm thoa là (440 ± 10) (Hz). Tốc độ truyền âm tại nơi làm thí nghiệm là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Chọn C + Ta có v=λf⇒→v=→λf=330m/s. → Sai số tuyệt đối của phép đo Δv=→v(Δλ→λ+Δf→f)=11,9m/s. → Viết kết quả v=330,0±11,9cm/s. Câu hỏi 33 : Từ hiện tượng tán sắc ánh và giao thoa ánh sáng, kết luận nào sau đây là đúng khi nói về chiết suất của một môi trường?
Đáp án: C Phương pháp giải: Chiết suất của mọi môi trường trong suốt có giá trị khác nhau đối với ánh sáng đơn sắc có màu khác nhau, giá trị nhỏ nhất đối với ánh sáng đỏ và giá trị lớn nhất đối với ánh sáng tím. Lời giải chi tiết: Phát biểu đúng là: Chiết suất của môi trường đối với những ánh sáng có bước sóng ngắn thì lớn hơn. Chọn C. Câu hỏi 34 : Với một âm có tần số xác định thì tốc độ lan truyền âm
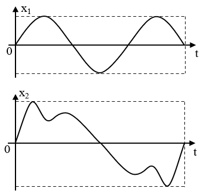
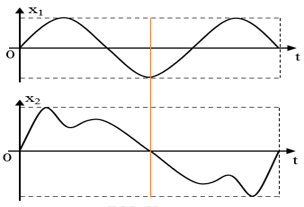
Đáp án: B Phương pháp giải: Vận tốc truyền âm trong các môi trường Lời giải chi tiết: Tốc độ truyền âm trong các môi trường là khác nhau, lớn nhất trong chất rắn, rồi đến chất lỏng và nhỏ nhất trong chất khí. Vì vậy với 1 âm có tần số xác đinh, vận tốc truyền âm nhanh nhất trong chất rắn. Câu hỏi 35 : Hai nhạc cụ phát ra hai âm có đồ thị dao động mô tả như hình bên. Chọn phát biểu đúng
Đáp án: A Phương pháp giải: + Đọc đồ thị + Vận dụng lí thuyết về họa âm Lời giải chi tiết:
Từ đồ thị, ta thấy chu kì của âm 2 lớn hơn âm 1 → tần số của âm 1 lớn hơn âm 2 → độ cao của âm 1 lớn hơn âm 2 Chọn A. Câu hỏi 36 : Trong bài thực hành xác định tốc độ truyền âm, một học sinh đo được bước sóng của âm là λ=(77,0±0,5)cm . Biết tần số nguồn âm là f = (440±10)HzHz. Tốc độ truyền âm mà học sinh này đo được trong thí nghiệm là:
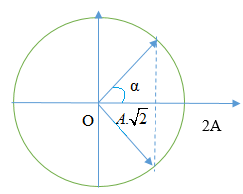
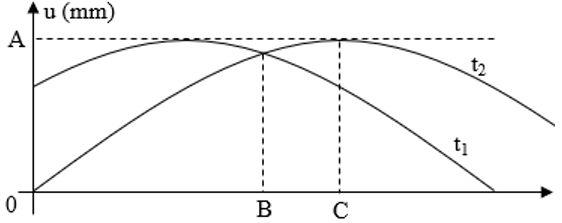
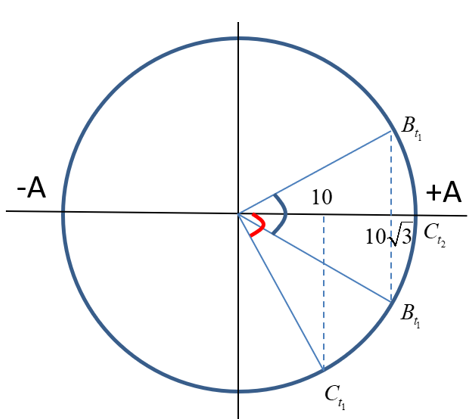
Đáp án: B Phương pháp giải: Cách ghi giá trị đo: Giá trị đo = giá trị trung bình sai số Công thức tính bước sóng: λ = v/f Vậy nên Δv = f.Δλ + λ.Δf Lời giải chi tiết: Giá trị trung bình của bước sóng là 77cm = 0,77m, của tần số là 440Hz. Giá trị trung bình của vận tốc: v = λf = 0,77.440 = 338,8m/s ≈ 339m/s Sai số của phép đo bước sóng và tần số lần lượt là 0,5cm = 0,005m và 10Hz Sai số của vận tốc thu được là Δv = f.Δλ + λ.Δf = 440.0,005 + 0,77.10 = 9,9m/s ≈10m/s Vậy tốc độ truyền âm thu được trong thí nghiệm là: (339±10)m/s Câu hỏi 37 : Trên một sợi dây dài, đang có sóng ngang truyền qua. Hình dạng của một đoạn dây tại hai thời điểm t1 và t2 như hình vẽ. Li độ của các phần tử tại B và C ở thời điểm t1 lần lượt là 10√3mm và10mm. Biết Δt=t2−t1=0,056s và nhỏ hơn một chu kì sóng. Tốc độ dao động cực đại của các phần tử trên dây bằng
Đáp án: C Phương pháp giải: + Đọc đồ thị + Sử dụng vòng tròn lượng giác Lời giải chi tiết: Từ đồ thị, xác định các điểm B, C tại thời điểm t1,t2 trên vòng tròn lượng giác, ta có: Ta có: ΔφC(t1→t2)=ΔφB(t1→t2)=α=ω.Δt Từ vòng tròn lượng giác, ta có: {cosα=10Acosα2=10√3A Từ đây ta suy ra cosα=12⇒α=600=π3 ⇒A=20mm Lại có: α=ω.Δt⇒ω=αΔt=π30,056=40π(rad/s) Tốc độ dao động cực đại của các phần tử dao động trên dây: vmax=Aω=20.40π=800π(mm/s)=0,8π(m/s) Chọn C Câu hỏi 38 : Hai nguồn âm nhỏ giống nhau phát ra âm thanh cùng pha cùng biên độ và cùng tần số tại A và B. Tai một người ở điểm N với AN=2m và BN=1,625m. Tốc độ truyền âm trong không khí là 330 m/s . Bước sóng dài nhất để người này không nghe được âm thanh từ hai nguồn phát ra là
Đáp án: B Phương pháp giải: Áp dụng điều kiện cực tiểu giao thoa d2−d1=(k+12)λ Lời giải chi tiết: Đáp án B + Để người này không nghe được âm thì N tương ứng là một cực tiểu giao thoa → AN−BN=(k+12)λ→ λ=AN−BNk+0,5. + Bước sóng lớn nhất ứng với k=0→ λ=AN−BN0,5=2−1,6250,5=0,75m |