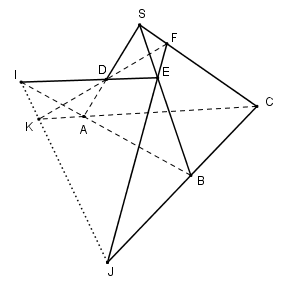
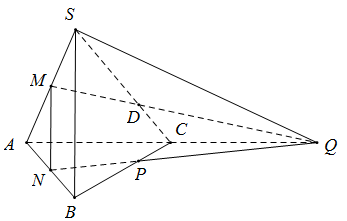
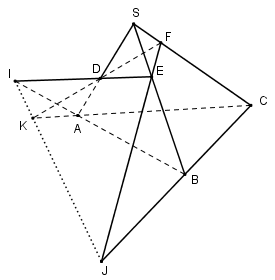
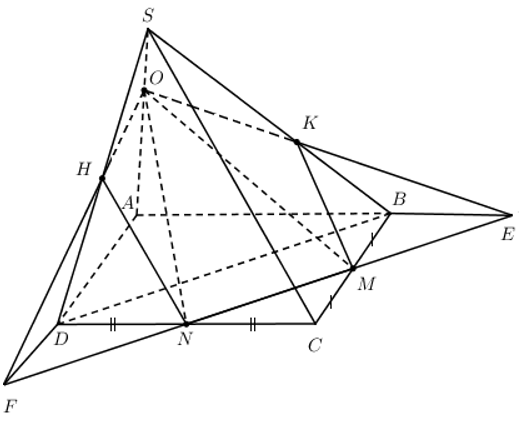
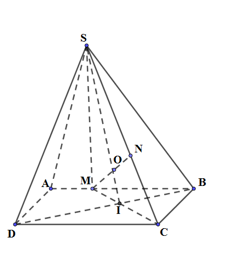
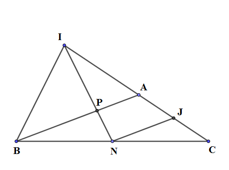
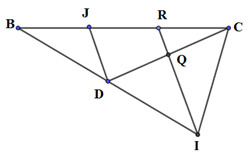
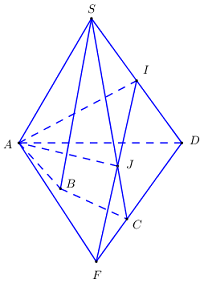
50 bài tập đại cương về đường thẳng và mặt phẳng mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Cho tứ diện SABC. Trên các cạnh SA, SB và SC lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt AC tại K. Chọn khẳng định sai?
Đáp án: D Phương pháp giải: Suy ra trục tiếp từ các đáp án. Lời giải chi tiết: Dễ thấy A và C đúng.
Ta có: \(\left\{ \begin{array}{l}I,J,K \in \left( {DEF} \right)\\I,J,K \in \left( {ABC} \right)\end{array} \right. \Rightarrow I,J,K \in \left( {DEF} \right) \cap \left( {ABC} \right).\) Mà giao tuyến của hai mặt phẳng là 1 đường thẳng nên I, J, K cùng thuộc một đường thẳng. Suy ra I, J, K thẳng hàng. Suy ra B đúng. Vậy D sai. Chọn D. Câu hỏi 2 : Cho tứ diện ABCD. Gọi P, Q, R, S lần lượt là các điểm trên cạnh AB, BC, CD và DA. Nếu 4 điểm P, Q R, S đồng phẳng. Chọn khẳng định sai?
Đáp án: C Phương pháp giải: Ba mặt phẳng cắt nhau theo giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc song song. Lời giải chi tiết:
Gọi mặt phẳng (PQRS) là mp(P) ta có: \(\left\{ \begin{array}{l}\left( P \right) \cap \left( {ABC} \right) = PQ\\\left( P \right) \cap \left( {ACD} \right) = RS\\\left( {ABC} \right) \cap \left( {ACD} \right) = AC\end{array} \right. \Rightarrow \) PQ, RS, AC hoặc song song hoặc đồng quy. Vậy A đúng. Tương tự ta có: \(\left\{ \begin{array}{l}\left( P \right) \cap \left( {ABD} \right) = PS\\\left( P \right) \cap \left( {BCD} \right) = QR\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\end{array} \right. \Rightarrow \) PS, RQ và BD đồng quy hoặc song song. Vậy B đúng. Dễ thấy đáp án D đúng. Vậy C sai. Chọn C. Câu hỏi 3 : Cho tứ diện ABCD. Gọi I, J là trung điểm của AC và AD. Xét các mệnh đề sau: (I) IJ // (BCD). (II) CD // (BCD) (III) Giao tuyến của (BCD) và (BIJ) là đường thẳng qua B song song với CD.
Đáp án: C Phương pháp giải: Suy ra trục tiếp từ các đáp án. Lời giải chi tiết:
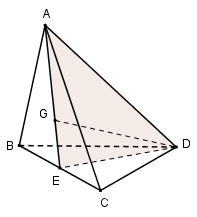
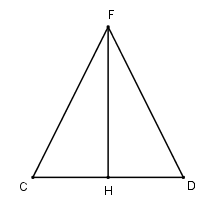
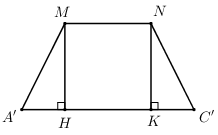
Ta có: IJ là đường trung bình của tam giác ACD nên IJ // CD suy ra \(\text{IJ}\parallel \left( BCD \right)\Rightarrow \) (I) đúng. (II) sai vì \(CD\subset \left( BCD \right).\) Ta có: \(\left\{ \begin{array}{l}B \in \left( {BCD} \right) \cap \left( {BIJ} \right)\\CD \subset \left( {BCD} \right)\\IJ \subset \left( {BIJ} \right)\\CD\parallel IJ\end{array} \right. \Rightarrow \)Giao tuyến của hai mặt phẳng (BCD) và (BIJ) là đường thẳng qua B và song song với CD, IJ suy ra (III) đúng. Chọn C. Câu hỏi 4 : Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mp(GAD) cắt tứ diện theo một thiết diện có diện tích bằng:
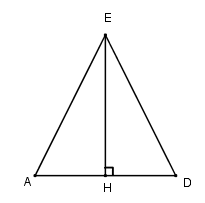
Đáp án: A Phương pháp giải: Chứng minh thiết diện là tam giác cân. Kẻ đường cao và tính diện tích tam giác cân đó. Lời giải chi tiết: Gọi E là trung điểm của BC dễ thấy AED là thiết diện của hình chóp khi cắt bởi mp(GAD). Ta có tam giác ABC và tam giác BCD là tam giác đều cạnh a nên \(AE=DE=\dfrac{a\sqrt{3}}{2}.\) AD = a. Gọi H là trung điểm của AD suy ra \(EH \bot AD\). Ta có: \(\begin{array}{l}EH = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 2 }}{2}\\ \Rightarrow {S_{EAD}} = \frac{1}{2}EH.AD = \dfrac{1}{2}\frac{{a\sqrt 2 }}{2}.a = \dfrac{{{a^2}\sqrt 2 }}{4}\end{array}\) Chọn A. Câu hỏi 5 : Cho S.ABCD có đáy là hình bình hành. Gọi M, N, Q lần lượt là trung điểm của BC, CD và SA. Thiết diện của mp(MNQ) với hình chóp là:
Đáp án: C Phương pháp giải: Xác định giao tuyến của mặt phẳng (MNQ) với các mặt của hình chóp bằng cách xác định các điểm chung. Lời giải chi tiết:
Trong (ABCD) kéo dài MN cắt AB tại E và cắt AD tại F. Trong (SAB) gọi \(H=QE\cap SB\) Trong (SAD) gọi \(G=QF\cap SD.\) Ta có: \(\begin{array}{l}\left( {MNQ} \right) \cap \left( {ABCD} \right) = MN\\\left( {MNQ} \right) \cap \left( {SAB} \right) = HQ\\\left( {MNQ} \right) \cap \left( {SAB} \right) = HM\\\left( {MNQ} \right) \cap \left( {SCD} \right) = NG\\\left( {MNQ} \right) \cap \left( {SAD} \right) = GQ\end{array}\) Vậy thiết diện của mặt phẳng (MNQ) và chóp là ngũ giác MNGQH. Chọn C. Câu hỏi 6 : Cho hình chóp S.ABCD có đáy ABCD là một tứ giác (AB không song song với CD). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB sao cho SN = 2NB, O là giao điểm của AC và BD. Cặp đường thẳng nào sau đây cắt nhau:
Đáp án: A Phương pháp giải: Hai đường thẳng cắt nhau chỉ khi chúng đồng phẳng và không song song. Lời giải chi tiết:
Ta thấy chỉ có MN và SO cùng thuộc mp(SBD) và không song song (vì \(\frac{SM}{SD}\ne \frac{SN}{SB}\)) nên MN và SO cắt nhau. Chọn A. Câu hỏi 7 : Cho hình chóp S.ABCD có đáy hình bình hành. Gọi M, N, Q lần lươt là trung điểm của BC, CD, SA. Thiết diện của (MNQ) với hình chóp là:
Đáp án: C Phương pháp giải: - Đưa về cùng mặt phẳng. - Xác định giao tuyến của (MNQ) với tất cả các mặt của hình chóp. Lời giải chi tiết:
Trong (ABCD) gọi \(E=MN\cap AB,F=MN\cap AD\Rightarrow E\in \left( SAB \right),F\in \left( SAD \right)\). Trong (SAB) gọi \(H=QE\cap SB.\)Trong (SAD) gọi \(G=QF\cap SD.\) Ta có: \(\begin{array}{l}\left( {MNQ} \right) \cap \left( {ABCD} \right) = MN\\\left( {MNQ} \right) \cap \left( {SAB} \right) = HQ\\\left( {MNQ} \right) \cap \left( {SBC} \right) = HM\\\left( {MNQ} \right) \cap \left( {SCD} \right) = NG\\\left( {MNQ} \right) \cap \left( {SAD} \right) = GQ.\end{array}\) Vậy thiết diện cần tìm là ngũ giác MNGQH. Chọn C.
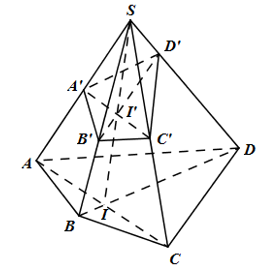
Câu hỏi 8 : Cho hình chóp S.ABCD. Một mặt phẳng không đi qua đỉnh nào của hình chóp cắt các cạnh SA, SB, SC, SD lần lượt tại các điểm A’, B’, C’, D’. Gọi O là giao điểm của AC và BD. Tìm mệnh đề đúng trong các mệnh đề sau:
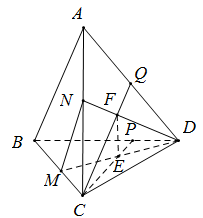
Đáp án: A Phương pháp giải: Sử dụng tính chất: Giao tuyến của 3 mặt phẳng phân biệt hoặc song song hoặc đồng quy. Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}\left( {A'B'C'D'} \right) \cap \left( {SAC} \right) = A'C'\\\left( {A'B'C'D'} \right) \cap \left( {SBD} \right) = B'D'\\\left( {SAC} \right) \cap \left( {SBD} \right) = SO\end{array} \right. \Rightarrow A'C';B'D';SO\)song song hoặc đồng quy. Mà SO và A’C’ không thể song song. Vậy các đường thẳng A’C’, B’D’, SO đồng quy. Chọn A. Câu hỏi 9 : Cho tứ diện ABCD. E, F lần lượt là các điểm nằm trong các tam giác BCD và ACD. M, N, P, Q lần lượt là giao của DE và BC, DF và AC, CE và BD, CF và AD. Khi đó giao điểm của EF và (ABC) là:
Đáp án: D Phương pháp giải: + Tìm một mặt phẳng thích hợp chứa EF + Tìm giao tuyến của mặt phẳng đó với (ABC) + Tìm giao điểm của giao tuyến đó với EF Lời giải chi tiết:
Ta có \(EF \subset \left( {DEF} \right) \Rightarrow EF \subset \left( {DMN} \right)\) \(\left( {DMN} \right) \cap \left( {ABC} \right) = MN\) Gọi I là giao điểm của EF và MN ⇒ I là giao của EF và (ABC) Chọn đáp án D Câu hỏi 10 : Cho hình chóp S.ABC. M, N lần lượt là trung điểm SA, AB. P nằm trên cạnh BC sao cho BP = 2PC. Giao điểm I của SC và (MNP) là:
Đáp án: C Phương pháp giải: + Tìm một mặt phẳng thích hợp chứa SC + Tìm giao tuyến của mặt phẳng đó với (MNP) + Tìm giao điểm của giao tuyến đó với SC Lời giải chi tiết:
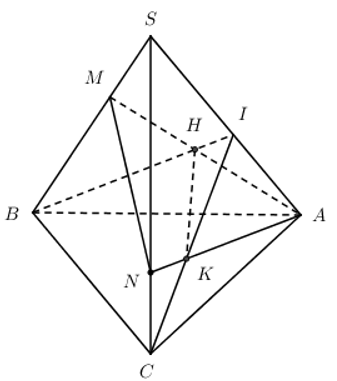
Có SC ⊂ (SAC) Gọi Q là giao điểm của NP và AC: ⇒ (MNP) ∩ (SAC) = MQ Gọi D là giao MQ và SC ⇒ D là giao của SC và (MNP) Chọn đáp án C Câu hỏi 11 : Cho tứ diện SABC. Trên các cạnh SA, SB và SC lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt AC tại K. Chọn khẳng định sai?
Đáp án: D Phương pháp giải: Suy ra trực tiếp từ các đáp án. Lời giải chi tiết:
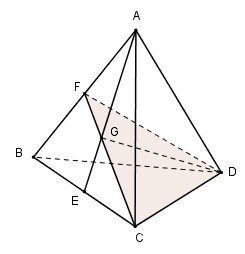
Dễ thấy A và C đúng. Ta có: \(\left\{ \matrix{ I,J,K \in \left( {DEF} \right) \hfill \cr I,J,K \in \left( {ABC} \right) \hfill \cr} \right. \Rightarrow I,J,K \in \left( {DEF} \right) \cap \left( {ABC} \right).\) Mà giao tuyến của hai mặt phẳng là 1 đường thẳng nên I, J, K cùng thuộc một đường thẳng. Suy ra I, J, K thẳng hàng. Suy ra B đúng. Vậy D sai. Chọn D. Câu hỏi 12 : Cho tứ diện ABCD có các cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Cắt tứ diện bới mp(GCD) thì diện tích của thiết diện là:
Đáp án: B Phương pháp giải: - Dựng thiết diện của hình chóp khi cắt bởi mp(GCD). - Chứng minh thiết diện là tam giác cân. Tính diện tích tam giác cân đó bằng cách kẻ thêm đường cao. Lời giải chi tiết:
Trong (ABC) gọi \(F=CG\cap AB\) ta có: \(\begin{array}{l}\left( {GCD} \right) \cap \left( {ABC} \right) = CF,\\\left( {GCD} \right) \cap \left( {ABD} \right) = DF\\\left( {GCD} \right) \cap \left( {BCD} \right) = CD\end{array}\) Vậy thiết diện là tam giác FCD. Tam giác ABC và ABD là tam giác đều cạnh a nên \(FC=FD=\frac{a\sqrt{3}}{2}\Rightarrow \Delta FCD\)cân tại F. Kẻ \(FH\bot CD\Rightarrow H\) là trung điểm của CD. Xét tam giác vuông FCH có: \(FH=\sqrt{F{{C}^{2}}-C{{H}^{2}}}=\sqrt{\frac{3{{a}^{2}}}{4}-\frac{{{a}^{2}}}{4}}=\frac{a\sqrt{2}}{2}.\) \(\Rightarrow{{S}_{FCD}}=\frac{1}{2}FH.CD=\frac{1}{2}\frac{a\sqrt{2}}{2}.a=\frac{{{a}^{2}}\sqrt{2}}{4}.\) Chọn B.
Câu hỏi 13 : Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD và OC. Gọi giao điểm của (MNP) với SA là K. Tỉ số \(\frac{KS}{KA}\) là:
Đáp án: B Phương pháp giải: +) Gọi E là giao điểm của SO và MN, khi đó giao điểm của (MNP) và SA là giao điểm của PE và SA. +) Áp dụng định lí Menelaus trong tam giác SAO: \(\frac{KS}{KA}.\frac{PA}{PO}.\frac{EO}{ES}=1\) +) Tính các tỉ số \(\frac{PA}{PO},\frac{EO}{ES}\) sau đó suy ra tỉ số \(\frac{KS}{KA}\). Lời giải chi tiết: Trong (SBD) gọi \(E=MN\cap SO\) \(\Rightarrow E\in MN\Rightarrow E\in \left( MNP \right)\Rightarrow PE\subset \left( MNP \right)\) Trong (SAC) gọi \(K=PE\cap SA\). Mà \(PE\subset \left( MNP \right)\Rightarrow \left( MNP \right)\cap SA=K\) Áp dụng định lí Menelaus trong tam giác SAO ta có: \(\frac{KS}{KA}.\frac{PA}{PO}.\frac{EO}{ES}=1\,\,\,\left( * \right)\) P là trung điểm của OC nên \(\frac{PA}{PO}=3\) Vì MN là đường trung bình của tam giác SBD \(\Rightarrow \) E là trung điểm của SO \(\Rightarrow \frac{EO}{ES}=1\) Thay vào (*) ta có \(\frac{KS}{KA}.3.1=1\Leftrightarrow \frac{KS}{KA}=\frac{1}{3}\) Chọn B.
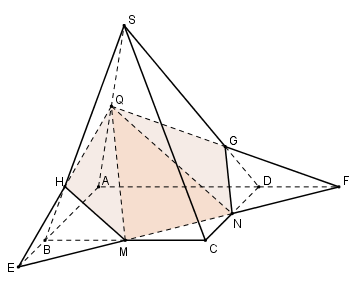
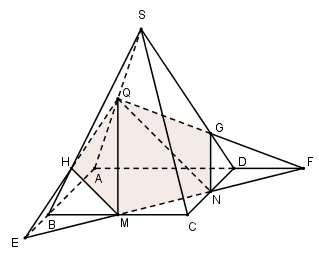
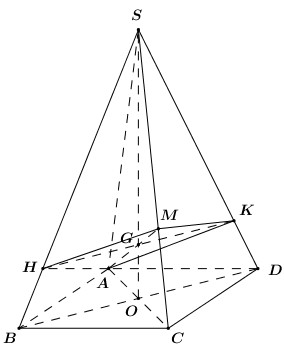
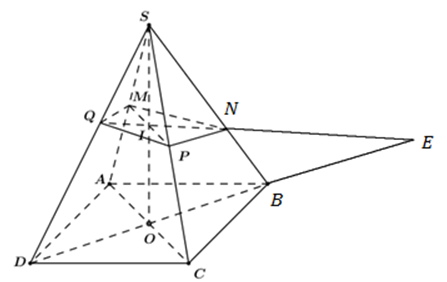
Câu hỏi 14 : Cho hình chóp đều SABCD có tất cả các cạnh bằng a, điểm M thuộc cạnh SC sao cho \(SM=2MC.\) Mặt phẳng (P) chứa AM và song song với BD. Tính diện tích thiết diện của hình chóp SABCD cắt bởi (P).
Đáp án: C Phương pháp giải: +) Hình chóp SABCD có tất các các cạnh bằng nhau nên tứ giác đáy là hình vuông và hình chiếu của S trên (ABCD) là tâm ) của hình vuông đáy. +) Gọi K là giao điểm của AM và SO. Qua K kẻ đường thẳng song song với DB, cắt SB tại E và SD tại K. Khi đó thiết diện là tứ giác ANMF. Lời giải chi tiết: Gọi K là giao điểm của AM và SO. Qua K kẻ đường thẳng song song với DB, cắt SB tại E và SD tại K. Khi đó thiết diện là tứ giác ANMF. Áp dụng định lí Menelaus cho tam giác SOC ta có: \(\frac{MS}{MC}.\frac{AC}{AO}.\frac{KO}{KS}=1\Leftrightarrow 2.2.\frac{KO}{KS}=1\Leftrightarrow \frac{KO}{KS}=\frac{1}{4}\) EF // BD \(\Rightarrow \frac{EF}{BD}=\frac{SK}{SO}=\frac{4}{5}\Rightarrow EF=\frac{4}{5}BD=\frac{4a\sqrt{2}}{5}\) Xét tam giác SAC có: \(S{{A}^{2}}+S{{A}^{2}}={{a}^{2}}+{{a}^{2}}=2{{a}^{2}}=A{{C}^{2}}\Rightarrow \Delta SAC\) vuông tại A \(\Rightarrow AM=\sqrt{S{{A}^{2}}-S{{M}^{2}}}=\sqrt{{{a}^{2}}+{{\left( \frac{2a}{3} \right)}^{2}}}=\frac{a\sqrt{13}}{3}\) Ta dễ dàng chứng minh được \(\Delta SAB=\Delta SAD\,\,\left( c.c.c \right)\Rightarrow AE=AF\Rightarrow \Delta AEF\) cân tại A, mà K là trung điểm của EF nên \(AK\bot EF\Rightarrow \) Tứ giác AEMF có \(AM\bot EF\Rightarrow {{S}_{AEMF}}=\frac{1}{2}AM.EF=\frac{1}{2}.\frac{a\sqrt{13}}{3}.\frac{4a\sqrt{2}}{5}=\frac{2{{a}^{2}}\sqrt{26}}{15}\) Chọn C. Câu hỏi 15 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thỏa mãn \(\overrightarrow{MA}=3\overrightarrow{MB}\). Mặt phẳng (P) qua M và song song với hai đường thẳng SC,BD. Mệnh đề nào sau đây đúng:
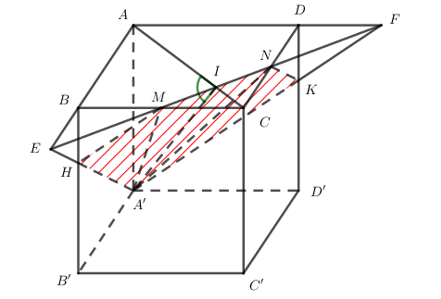
Đáp án: C Phương pháp giải: Lời giải chi tiết: Câu hỏi 16 : Cho hình hộp \(ABCD.A'B'C'D’\) , và một điểm M nằm giữa hai điểm A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AB’D’). Cắt hình hộp bởi mặt phẳng (P) thì thiết diện là :
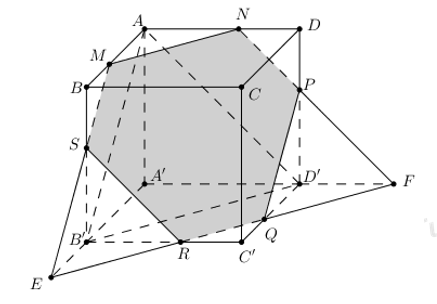
Đáp án: B Phương pháp giải: Xác định thiết diện dựa vào các yếu tố song song. Lời giải chi tiết:
\(\begin{align} \left( P \right)//B'D'//BD\subset \left( ABCD \right)\Rightarrow \left( P \right)\cap \left( ABCD \right)=MN//BD\,\,\left( N\in BC \right) \\ \left( P \right)//AD'\subset \left( ADD'A' \right)\Rightarrow \left( P \right)\cap \left( ADD'A' \right)=NP//AD'\,\,\left( P\in DD' \right) \\ \left( P \right)//AB'\subset \left( ABB'A' \right)\Rightarrow \left( P \right)\cap \left( ABB'A' \right)=MS//AB'\,\,\left( S\in BB' \right) \\ \end{align}\) Trong (ABB’A’), gọi \(E=MS\cap A'B’\) , trong (ADD’A’), gọi \(F=NP\cap A'D’\) . Trong \(\left( A'B'C'D' \right):\,\,EF\cap B'C'=R;\,\,EF\cap C'D'=Q\) Vậy thiết diện của hình lập phương khi cắt bởi mặt phẳng \(\left( P \right)\) là lục giác \(MNPQRS\) Chọn B. Câu hỏi 17 : Cho hình chóp SABC. \(M\in SB,\,N\in SC,\,I\in SA.\) Tìm giao tuyến của hai mặt phẳng (AMN) và (IBC). Phương pháp giải: Lời giải chi tiết: +) Nối \(IB\cap MA=H\Rightarrow \) H chung. +) Nối \(IC\cap NA=K\Rightarrow K\) chung. +) \(\Rightarrow \left( IBC \right)\cap \left( AMN \right)=HK\) Câu hỏi 18 : Cho hình chóp SABCD. ABCD là hình thang. AB // CD. M là trung điểm của SA, \(N\in SD\) để \(NS=2ND.\,\,\,P\in AB.\) Tìm giao tuyến \(\left( MNP \right)\) và \(\left( SBD \right)\) Phương pháp giải: Lời giải chi tiết: +) Ta có: N chung +) Nối \(MN\cap AD=E\) +) Nối \(EP\cap BD=H\Rightarrow H\) chung. +) \(\left( MNP \right)\cap \left( SBD \right)=NH.\) Câu hỏi 19 : Chóp SABC. \(M\in SB,\,N\in SC.\) O thuộc miền trong tam giác ABC. Tìm giao điểm của MN và mặt phẳng (SAC). Phương pháp giải: Lời giải chi tiết: +) Bước 1: Cho \(MN\subset \left( SBC \right)\) +) Bước 2: Nối \(AO\cap BC=E\Rightarrow \left( SAO \right)\cap \left( SBC \right)=SE\) +) Bước 3: Nối \(SE\cap MN=G\) \(\Rightarrow\) G là giao điểm cần tìm Câu hỏi 20 : Chóp SABCD. \(M\in SB,\,N\in SD.\) Tìm giao điểm MN và (SAC). Phương pháp giải: Lời giải chi tiết: +) Bước 1: Cho \(MN\subset \left( SBD \right)\) +) Bước 2: Nối \(AC\cap BD=O\Rightarrow \left( SAC \right)\cap \left( SBD \right)=SO\) +) Bước 3: Nối \(SO\cap MN=G\) \(\Rightarrow\) G là giao điểm cần tìm. Câu hỏi 21 : Chóp SABCD. ABCD là hình bình hành. M, N lần lượt là trung điểm của BC, CD. \(O\in SA\) để \(OA=2OS.\) Tìm thiết diện (MNO) và chóp SABCD. Phương pháp giải: Lời giải chi tiết: +) Bước 1: Có sẵn \(\left( MNO \right)\cap \left( ABCD \right)=MN\) +) Bước 2: Nối \(MN\cap AB=E,\,MN\cap AD=F\) Nối \(OE\cap SB=K,\,OF\cap SD=H\) Ta có: \(\left\{ \begin{align} & \left( OEF \right)\cap \left( SBC \right)=MK \\ & \left( OEF \right)\cap \left( SAB \right)=KC \\ & \left( OEF \right)\cap \left( SAD \right)=OH \\ & \left( OEF \right)\cap \left( SCD \right)=HN \\\end{align} \right.\) +) Bước 3: Thiết diện là ngũ giác MNHOK.
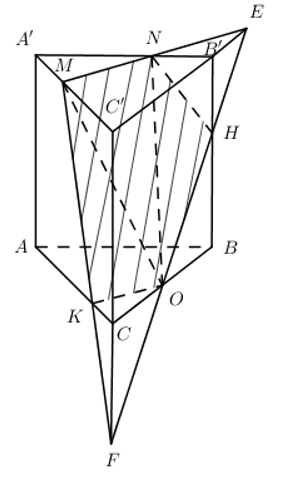
Câu hỏi 22 : Chóp SABCD. AB không song song với CD. \(M\in SA\) sao cho MA = 2MS. Tìm thiết diện \(\left( MCD \right)\) và chóp SABCD. Phương pháp giải: Lời giải chi tiết: +) Bước 1: Ta có: \(\left( MCD \right)\cap \left( ABCD \right)=CD,\,\,\left( MCD \right)\cap \left( SCD \right)=CD\) +) Bước 2: Nối \(CD\cap AB=E,\,\,ME\cap SB=N\) Ta có: \(\left\{ \begin{array}{l} +) Bước 3: Thiết diện là tứ giác MNCD. Câu hỏi 23 : Cho chóp SABC. \(M\in SC\) sao cho MC = 2MS. \(N\in SB\) để NS = 2NB. \(O\in \Delta ABC.\) Tìm thiết diện của (MNO) và chóp. Phương pháp giải: Lời giải chi tiết: +) Bước 1: \(\left( OMN \right)\cap \left( SBC \right)=MN\) +) Bước 2: Nối \(MN\cap BC=E,\,\,OE\cap AB=H,\,\,OE\cap AC=K\) Ta có: \(\left\{ \begin{align} & \left( MKE \right)\cap \left( SAB \right)=NH \\ & \left( MKE \right)\cap \left( ABC \right)=HK \\ & \left( MKE \right)\cap \left( SAC \right)=KM \\\end{align} \right.\) +) Bước 3: Thiết diện là tứ giác MNHK. Câu hỏi 24 : Lăng trụ ABCA’B’C’. \(M\in A'C'\) sao cho C’M = 2MA’, \(N\in A'B'\) để NA’ = 2NB’. O là trung điểm của BC. Tìm thiết diện (MNO) với lăng trụ. Phương pháp giải: Lời giải chi tiết: +) Bước 1: \(\left( OMN \right)\cap \left( A'B'C' \right)=MN\) +) Bước 2: Nối \(MN\cap B'C'=E,\,\,OE\cap BB'=H,\,\,OE\cap CC'=F,\,MF\cap AC=K\) Ta có: \(\left\{ \begin{align} & \left( MEF \right)\cap \left( ABB'A' \right)=NH \\ & \left( MEF \right)\cap \left( BCC'B' \right)=HO \\ & \left( MEF \right)\cap \left( ABC \right)=OK \\ & \left( MEF \right)\cap \left( ACC'A' \right)=KM \\\end{align} \right.\)
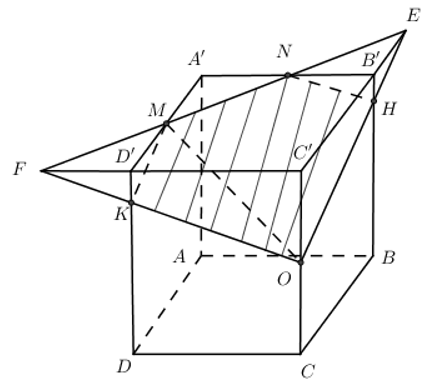
+) Bước 3: Thiết diện là ngũ giác MNHOK Câu hỏi 25 : Cho hình lập phương ABCDA’B’C’D’. M, N, O lần lượt là trung điểm của A’D’, A’B’, CC’. Tìm thiết diện của mặt phẳng (MNO) với hình lập phương. Phương pháp giải: Lời giải chi tiết: +) Bước 1: \(\left( MNO \right)\cap \left( A'B'C'D' \right)=MN\) +) Bước 2: Nối \(\begin{align} & MN\cap B'C'=E,\,MN\cap C'D'=F \\ & OE\cap BB'=H,\,OF\cap DD'=K \\\end{align}\) Ta có: \(\left\{ \begin{align} & \left( MNO \right)\cap \left( ABB'A' \right)=NH \\ & \left( MNO \right)\cap \left( BCC'B' \right)=HO \\ & \left( MNO \right)\cap \left( CDD'C' \right)=OK \\ & \left( MNO \right)\cap \left( ADD'A' \right)=KM \\\end{align} \right.\) +) Bước 3: Thiết diện là ngũ giác MNHOK Câu hỏi 26 : Cho hình chóp S.ABCD, đáy là hình bình hành ABCD, các điểm M và N lần lượt thuộc các cạnh AB, SC. Phát biểu nào sau đây đúng?
Đáp án: C Phương pháp giải: Lời giải chi tiết:
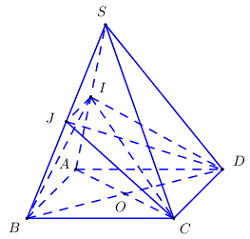
Trong (ABCD), gọi I là giao của CM với BD Khi đó, \(I \in BD \subset \left( {SBD} \right)\) và \(I \in MC \subset \left( {SMC} \right)\) Trong (SMC), gọi \(O = MN \cap SI\) Khi đó, \(\left\{ \begin{array}{l}O \in MN\\O \in SI \subset \left( {SBD} \right)\end{array} \right. \Rightarrow O = MN \cap \left( {SBD} \right)\) Vậy, giao điểm của MN với (SBD) là giao điểm của MN với SI, trong đó I là giao của CM với BD. Chọn: C Câu hỏi 27 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. M là trung điểm của SB và G là trọng tâm tam giác SAD. Gọi J là giao điểm của AD và mặt phẳng (OMG). Tính tỉ số \(\frac{{JA}}{{JD}}\).
Đáp án: C Phương pháp giải: Lời giải chi tiết:
Gọi I là trung điểm của AD Trong (SIB), gọi E là giao điểm của MG và BI Trong (ABCD), gọi J là giao điểm của BE và AB Khi đó, J là giao điểm của AD và (MOG) Xét tam giác SBE có: ME là trung tuyến đi qua G nằm trên SI mà \(\frac{{SG}}{{SI}} = \frac{2}{3} \Rightarrow I\) là trung điểm của BE và G là trọng tâm tam giác SBE Xét tam giác EBC có: I là trung điểm BE, ID//BC \( \Rightarrow \) Đường thẳng ID cắt cạnh CE tại trung điểm của CE Mà \(ID = \frac{1}{2}BC \Rightarrow ID\)là đường trung bình của tam giác EBC, D là trung điểm của CE Xét tam giác ACF: AD, EO là trung tuyến, \(J = AD \cap OE \Rightarrow J\)là trọng tâm tam giác ACF \( \Rightarrow \frac{{JA}}{{JD}} = 2\). Chọn: C Câu hỏi 28 : Một hình chóp có tổng số đỉnh và số cạnh bằng 13. Tìm số cạnh của đa giác đáy.
Đáp án: A Phương pháp giải: Giả sử hình chóp có n cạnh bên. Khi đó, số đỉnh là \(n + 1\), số cạnh là \(2n\). Lời giải chi tiết: Giả sử hình chóp có n cạnh bên. Khi đó, số đỉnh là \(n + 1\), số cạnh là \(2n\). Theo đề bài, ta có: \(n + 1 + 2n = 13 \Leftrightarrow 3n = 12 \Leftrightarrow n = 4\) Số cạnh của đa giác đáy là 4. Chọn: A Câu hỏi 29 : Cho hình chóp S.ABCD. Một mặt phẳng \(\left( P \right)\) bất kì cắt các cạnh SA, SB, SC và SD lần lượt tại A’, B’, C’, D’. Gọi I là giao điểm của AC và BD. Chọn khẳng định đúng trong các khẳng định dưới đây?
Đáp án: C Phương pháp giải: Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau. Lời giải chi tiết:
Ta có: \(\begin{array}{l}\left( {A'B'C'D'} \right) \cap \left( {SAC} \right) = A'C'\\\left( {A'B'C'D'} \right) \cap \left( {SBD} \right) = B'D'\\\left( {SAC} \right) \cap \left( {SBD} \right) = SI\end{array}\)
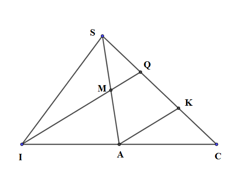
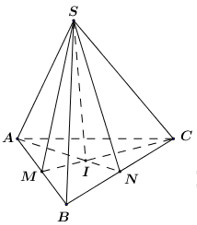
Do đó các đường thẳng A’C’, B’D’, SI đồng quy hoặc song song, hoặc đồng quy. Xét trong mặt phẳng (SAC) có A’C’ và SI không song song, do đó các đường thẳng A’C’, B’D’, SI đồng quy. Chọn đáp án C. Câu hỏi 30 : Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA, BC và P là điểm nằm trên cạnh AB sao cho \(AP = \frac{1}{3}AB\). Gọi Q là giao điểm của \(SC\) và \(\left( {MNP} \right)\). Tính tỉ số \(\frac{{SQ}}{{SC}}\).
Đáp án: C Phương pháp giải: Lời giải chi tiết:
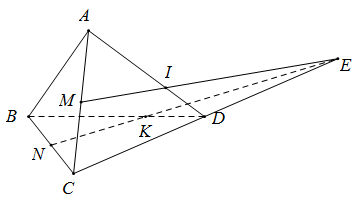
Do \(\frac{{AP}}{{AB}} = \frac{1}{3},\,\,\frac{{CN}}{{CB}} = \frac{1}{2} \Rightarrow NP\) không song song với AC Trong \(\left( {ABC} \right)\), gọi \(I = NP \cap AC\) Trong \(\left( {SAC} \right)\), gọi \(Q = IM \cap SC\). Do \(IM \subset \left( {MNP} \right)\) \( \Rightarrow Q = SC \cap \left( {MNP} \right)\) *) Xét \(\Delta IBC\): Kẻ NJ song song AB, (\(J \in IC\)) . Do N là trung điểm của BC \( \Rightarrow J\) là trung điểm của AC \( \Rightarrow AC = 2AJ\) Ta có: \(\left\{ \begin{array}{l}AP//NJ\\\frac{{IP}}{{NP}} = 2\end{array} \right. \Rightarrow \frac{{IA}}{{AJ}} = 2 \Rightarrow AI = 2AJ\,\, \Rightarrow IA = AC = \left( {2AJ} \right)\) \( \Rightarrow A\)là trung điểm của IC. *) Xét \(\Delta SIC\): Kẻ AK song song IQ, (\(K \in SC\)). Do A là trung điểm của IC \( \Rightarrow \) K là trung điểm của QC \( \Rightarrow QK = KC\) Ta có: \(MQ//AK,\,\,M\) là trung điểm của SA \( \Rightarrow Q\) là trung điểm của\(SK\) \( \Rightarrow SQ = QK\) \( \Rightarrow SQ = QK = KC\,\, \Rightarrow SQ = \frac{1}{3}SC \Rightarrow \frac{{SQ}}{{SC}} = \frac{1}{3}\). Chọn: C Câu hỏi 31 : Tứ diện ABCD. Gọi M là trung điểm của BC. N là điểm nằm trên đoạn thẳng AB sao cho NB = 2NA, P là điểm nằm trên đoạn thẳng CD sao cho \(PC = 3PD\), S là giao điểm của BD và MP, Q là giao điểm của SN và AD. Tính tỉ số \(\frac{{QD}}{{QA}}\).
Đáp án: C Phương pháp giải: Sử dụng định lí Ta-lét. Lời giải chi tiết:
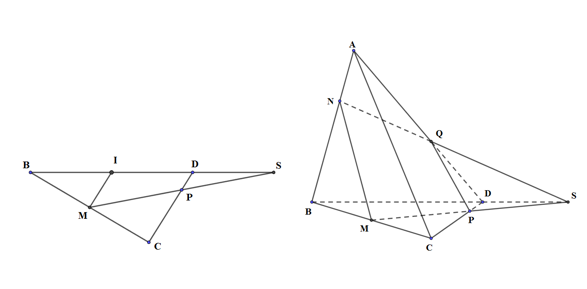
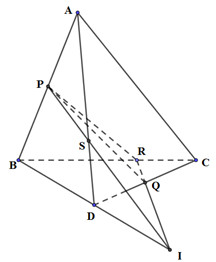
Gọi I là trung điểm của BD \( \Rightarrow \)IM là đường trung bình của tam giác BCD \( \Rightarrow IM//CD,\,\,IM = \frac{1}{2}CD\) Mà \(PD = \frac{1}{4}CD \Rightarrow PD = \frac{1}{2}IM \Rightarrow \) PD là đường trung bình của tam giác SIM \( \Rightarrow D\) là trung điểm của SI \( \Rightarrow BI = ID = SD \Rightarrow SD = \frac{1}{3}SB\) Xét tam giác SAB có: \(\frac{{AN}}{{AB}} = \frac{{SD}}{{SB}} = \frac{1}{3} \Rightarrow ND//SA\) và \(\frac{{ND}}{{SA}} = \frac{{NB}}{{AB}} = \frac{2}{3}\) \( \Rightarrow \frac{{QD}}{{QA}} = \frac{{ND}}{{SA}} = \frac{2}{3}\). Chọn: C Câu hỏi 32 : Cho tứ diện ABCD. P, Q lần lượt là trung điểm của AB, CD. Điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp (PQR) và AD. Khi đó:
Đáp án: B Phương pháp giải: +) Xác định giao điểm của (PQR) với các cạnh của tứ diện, xác định điểm D. +) Sử dụng định nghĩa và định lí đường trung bình chứng minh D là trung điểm của BI. Lời giải chi tiết:
Trong (BCD) gọi I là giao điểm của RQ và BD. Trong (ABD) gọi S là giao điểm của AD và IP Khi đó, \(S = AD \cap \left( {PQR} \right)\) *) Chứng mình D là trung điểm của BI:
Gọi J là trung điểm của BR. Do R nằm trên cạnh BC sao cho BR = 2RC \( \Rightarrow BJ = JR = RC\) Ta có: \(RQ\) là đường trung bình của tam giác JCD \( \Rightarrow RQ//JD\,\, \Rightarrow RI//JD\) Xét tam giác BRI có: J là trung điểm của BR, \(DJ//RI \Rightarrow D\) là trung điểm của BI. *) Xét tam giác ABI có: \(P,D\) lần lượt là trung điểm của AD, BI \(PI \cap AD = S \Rightarrow S\) là trọng tâm tam giác ABI \( \Rightarrow SA = 2SD\). Chọn: B Câu hỏi 33 : Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Goi I là giao điểm của BC với mặt phẳng (ADG). Tìm khẳng định sai ?
Đáp án: A Phương pháp giải: Xác định giao điểm của BC và (ADG). Lời giải chi tiết: Trong (ABC) gọi \(I = AG \cap BC\) ta có: \(\left\{ \begin{array}{l}I \in AG \Rightarrow I \in \left( {ADG} \right)\\I \in BC\end{array} \right. \Rightarrow I = BC \cap \left( {ADG} \right)\) . Vì G là trọng tâm tam giác ABC \( \Rightarrow I\) là trung điểm của BC. Vậy đáp án A sai. Chọn A.
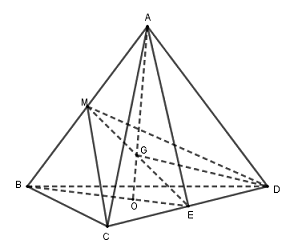
Câu hỏi 34 : Cho tứ diện \(ABCD\) đều cạnh a. Gọi G là trọng tâm tam giác ABC, mặt phẳng \(\left( {CGD} \right)\) cắt tứ diện theo một thiết diện có diện tích là:
Đáp án: C Phương pháp giải: Lời giải chi tiết:
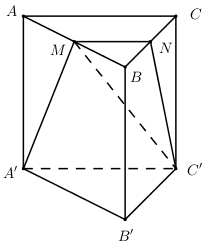
Gọi I, J lần lượt là trung điểm của AB, CD \( \Rightarrow I,G,C\) thẳng hàng \( \Rightarrow \left( {CGD} \right)\) cắt tứ diện ABCD bởi thiết diện là tam giác \(ICD\) Ta có: \(ID = IC = \dfrac{{a\sqrt 3 }}{2}\) (do là đường cao của các tam giác đều cạnh a) \( \Rightarrow \Delta ICD\) cân tại I \( \Rightarrow IJ \bot CD\) \(\Delta IJC\) vuông tại J \( \Rightarrow IJ = \sqrt {I{C^2} - J{C^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{2}\) Diện tích \(\Delta ICD\) là: \(S = \dfrac{1}{2}IJ.CD = \dfrac{1}{2}.\dfrac{{a\sqrt 2 }}{2}.a = \dfrac{{{a^2}\sqrt 2 }}{4}\). Chọn: C Câu hỏi 35 : Cho lăng trụ đều \(ABC.A'B'C'\) có cạnh đáy bằng \(a\), cạnh bên bằng \(\sqrt 2 a\). Gọi \(M\) là trung điểm \(AB\). Tính diện tích thiết diện cắt lăng trụ đã cho bởi mặt phẳng \(\left( {A'C'M} \right)\).
Đáp án: C Phương pháp giải: +) Xác định thiết diện dựa vào các yếu tố song song. Chứng minh thiết diện là hình thang cân. +) Tính diện tích hình thang cân. Lời giải chi tiết:
Gọi \(N\) là trung điểm của \(BC\) ta có \(MN\) là đường trung bình của tam giác \(ABC \Rightarrow MN//AC\). Ta có \(\left( {A'C'M} \right)\) chứa \(A'C'//AC \Rightarrow \left( {A'C'M} \right)\) cắt \(ABC\) theo giao tuyến là đường thẳng qua \(M\) và song song với \(AC \Rightarrow \left( {A'C'M} \right) \cap \left( {ABC} \right) = MN\). Vậy thiết diện của hình lăng trụ cắt bởi mặt phẳng \(\left( {A'C'M} \right)\) là tứ giác \(A'C'NM\). Ta có \(MN//AC//A'C' \Rightarrow A'C'NM\) là hình thang. Xét \(\Delta A'AM\) và \(\Delta C'CN\) có: \(A'A = C'C,\,\,\angle A'AM = \angle C'CM = {90^0};\,\,AM = CN = \dfrac{a}{2}\) \( \Rightarrow \Delta A'AM = \Delta C'CN\,\,\left( {c.g.c} \right) \Rightarrow A'M = C'N\). Dễ dàng nhận thấy \(A'M\) và \(C'N\) không song song nên \(A'C'NM\) là hình thang cân. Có \(A'C' = a;\,\,MN = \dfrac{a}{2}\).
Kẻ \(MH \bot A'C'\,\,\left( {H \in A'C'} \right);\,\,NK \bot A'C'\,\,\left( {K \in A'C'} \right)\) ta có \(MNKH\) là hình chữ nhật \( \Rightarrow MN = HK = \dfrac{a}{2}\). \( \Rightarrow A'H = C'K = \dfrac{{A'C' - HK}}{2} = \dfrac{{a - \dfrac{a}{2}}}{2} = \dfrac{a}{4}\). Xét tam giác vuông \(A'AM\) có \(A'M = \sqrt {A'{A^2} + A{M^2}} = \sqrt {2{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{3a}}{2}\) Xét tam giác vuông \(A'MH\) có : \(MH = \sqrt {A'{M^2} - A'{H^2}} = \dfrac{{9{a^2}}}{4} - \dfrac{{{a^2}}}{{16}} = \dfrac{{a\sqrt {35} }}{4}\). Vậy \({S_{A'C'NM}} = \dfrac{1}{2}\left( {A'C' + MN} \right).MH = \dfrac{1}{2}\left( {a + \dfrac{a}{2}} \right).\dfrac{{a\sqrt {35} }}{4} = \dfrac{{3\sqrt {35} {a^2}}}{{16}}\). Chọn C. Câu hỏi 36 : Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(\sqrt 3 .\) Mặt phẳng \(\left( \alpha \right)\) cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng \(\left( \alpha \right)\) biết \(\left( \alpha \right)\) tạo với mặt \(\left( {ABB'A'} \right)\) một góc \(60^\circ .\)
Đáp án: A Phương pháp giải: Ta sử dụng công thức diện tích hình chiếu \(S' = S.\cos \alpha \) Với \(S\) là diện tích hình \(H\), \(S'\)và là diện tích hình chiếu của \(H\) trên mặt phẳng \(\left( P \right)\), \(\alpha \) là góc tạo bởi mặt phẳng chứa hình \(H\) và mặt phẳng \(\left( P \right)\). Lời giải chi tiết:
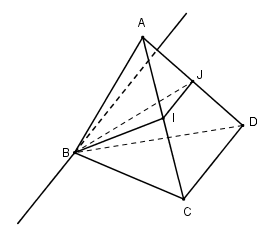
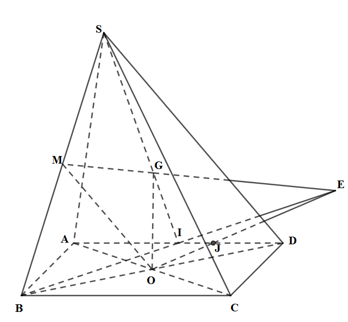
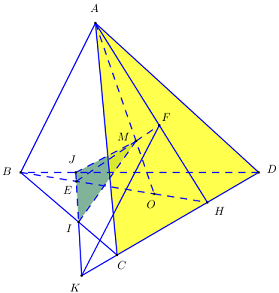
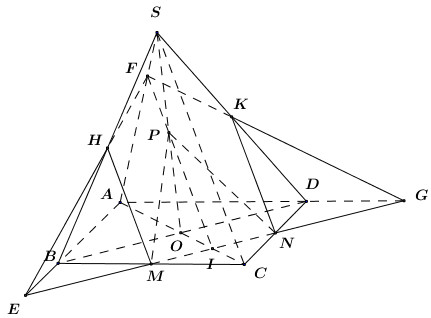
Mặt phẳng \(\left( \alpha \right)\) cắt các cạnh \(DD';AA';BB';CC'\) lần lượt tại \(E;F;G;H.\) Khi đó \(\left( \alpha \right) \equiv \left( {EFGH} \right)\) Vì \(ABCD.A'B'C'D'\) là hình lập phương nên \(\left( {ABB'A'} \right) \bot \left( {ABCD} \right)\) mà \(\left( {EFGH} \right)\) tạo với \(\left( {ABB'A'} \right)\) góc \(60^\circ \) nên góc giữa \(\left( {EFGH} \right)\) và \(\left( {ABCD} \right)\) là \(30^\circ .\) Lại có hình chiếu của \(EFGH\) xuống mặt phẳng \(\left( {ABCD} \right)\) là hình vuông \(ABCD\) cạnh \(\sqrt 3 .\) Theo công thức tính diện tích hình chiếu ta có \({S_{ABCD}} = {S_{EFGH}}.\cos 30^\circ \Rightarrow {S_{EFGH}} = \dfrac{{{{\left( {\sqrt 3 } \right)}^2}}}{{\cos {{30}^0}}} = 2\sqrt 3 .\) Chọn A. Câu hỏi 37 : Cho tứ diện \(ABCD\). Gọi \(O\) là một điểm nằm bên trong tam giác \(BCD\) và \(M\) là một điểm trên đoạn \(AO\). Gọi \(I,\,\,J\) là hai điểm trên cạnh \(BC,\,\,BD\). Giả sử \(IJ\) cắt \(CD\) tại \(K\), \(BO\) cắt \(IJ\) tại \(E\) và cắt \(CD\) tại \(H\), \(ME\) cắt \(AH\) tại \(F\). Giao tuyến của hai mặt phẳng \(\left( {MIJ} \right)\) và \(\left( {ACD} \right)\) là đường thẳng:
Đáp án: D Phương pháp giải: Xác định hai điểm chung của hai mặt phẳng. Lời giải chi tiết:
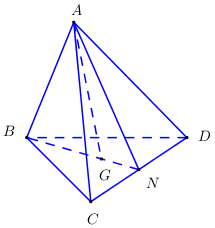
Trong \(\left( {MIJ} \right)\) kéo dài \(ME\) cắt \(AH\) tại \(F\). Ta có \(F = AH \cap ME \Rightarrow \left\{ \begin{array}{l}F \in AH \subset \left( {SCD} \right)\\F \in ME \subset \left( {MIJ} \right)\end{array} \right.\) \( \Rightarrow F \in \left( {SCD} \right) \cap \left( {MIJ} \right)\). Ta có \(\left\{ \begin{array}{l}K \in IJ \subset \left( {MIJ} \right)\\K \in CD \subset \left( {SCD} \right)\end{array} \right. \Rightarrow K \in \left( {MIJ} \right) \cap \left( {SCD} \right)\). Vậy \(\left( {MIJ} \right) \cap \left( {SCD} \right) = KF\). Chọn D Câu hỏi 38 : Cho tứ diện \(ABCD\). \(G\) là trọng tâm tam giác \(BCD\). Giao tuyến của hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right)\) là:
Đáp án: B Phương pháp giải: Xác định hai điểm chung của hai mặt phẳng. Lời giải chi tiết:
Gọi \(N\) là trung điểm của \(CD\). Do \(G\) là trọng tâm tam giác \(BCD \Rightarrow G \in BM\). Ta có \(\left\{ \begin{array}{l}A \in \left( {GAB} \right)\\N \in BG \subset \left( {GAB} \right) \Rightarrow N \in \left( {GAB} \right)\end{array} \right. \Rightarrow AN \subset \left( {GAB} \right)\). Dễ thấy \(AN \subset \left( {ACD} \right)\). Vậy \(\left( {GAB} \right) \cap \left( {ACD} \right) = AN\) với \(N\) là trung điểm của \(CD\). Chọn B Câu hỏi 39 : Cho hình chóp \(S.ABCD\). Gọi \(I\) là trung điểm của \(SD,\,\,J\) là điểm trên \(SC\) và không trùng trung điểm \(SC\). Giao tuyến của hai mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {AIJ} \right)\) là:
Đáp án: D Phương pháp giải: Xác định các điểm chung của hai mặt phẳng. Lời giải chi tiết:
Dễ thấy \(\left( {ABCD} \right)\) và \(\left( {AIJ} \right)\) có điểm chung thứ nhất là \(A\). Do \(J\) không là trung điểm của \(SC\) nên \(IJ\) không song song với \(CD\). Trong \(\left( {SCD} \right)\) gọi \(F = IJ \cap CD\) ta có: \(\left\{ \begin{array}{l}F \in CD \subset \left( {ABCD} \right)\\F \in IJ \subset \left( {AIJ} \right)\end{array} \right. \Rightarrow F \in \left( {ABCD} \right) \cap \left( {AIJ} \right)\). Suy ra \(\left( {ABCD} \right)\) và \(\left( {AIJ} \right)\) có điểm chung thứ hai là \(F\). Vậy \(\left( {ABCD} \right) \cap \left( {AIJ} \right) = AF\) với \(F = IJ \cap CD\). Chọn D Câu hỏi 40 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I,\,\,J\) lần lượt là trung điểm \(SA\) và \(SB\). Khẳng định nào sau đây là sai ?
Đáp án: D Phương pháp giải: Xác định các giao tuyến của từng cặp mặt phẳng ở từng đáp án. Lời giải chi tiết:
+ Ta có \(IJ\) là đường trung bình của \(\Delta SAB \Rightarrow IJ\parallel AB\). Mà \(AB\parallel CD\) (do \(ABCD\) là hình bình hành) nên \(IJ\parallel CD\). Do đó \(IJCD\) là hình thang nên đáp án A đúng. + Dễ thấy \(\left( {SAB} \right)\) và \(\left( {IBC} \right)\) có điểm chung thứ nhất là \(B\). \(\left\{ \begin{array}{l}I \in SA \subset \left( {SAB} \right)\\I \in \left( {IBC} \right)\end{array} \right. \Rightarrow I \in \left( {SAB} \right) \cap \left( {IBC} \right)\). \( \Rightarrow \left( {SAB} \right)\) và \(\left( {IBC} \right)\) có điểm chung thứ hai là \(I\). \( \Rightarrow \left( {SAB} \right) \cap \left( {IBC} \right) = IB\), do đó đáp án B đúng. + CMTT ta có \(\left( {SBD} \right) \cap \left( {JCD} \right) = JD\) do đó đáp án C đúng. + Đáp án D sai do \(A \notin \left( {JBD} \right)\). Chọn D Câu hỏi 41 : Cho hình chóp tứ giác \(S.ABCD\), \(M\) là một điểm trên cạnh \(SC,\,\,N\) là điểm trên cạnh \(BC\). Tìm giao điểm của hai đường thẳng \(SD\) với \(\left( {AMN} \right)\).
Đáp án: A Phương pháp giải: \(\left\{ \begin{array}{l}a \cap b = M\\b \subset \left( P \right)\end{array} \right. \Rightarrow a \cap \left( P \right) = M\). Lời giải chi tiết:
Ta có \(SD \subset \left( {SBD} \right)\), do đó ta tìm giao tuyến của \(\left( {AMN} \right)\) và \(\left( {SBD} \right)\). Trong \(\left( {ABCD} \right)\) gọi \(J = AN \cap BD \Rightarrow \left\{ \begin{array}{l}J \in AN \subset \left( {AMN} \right)\\J \in BD \subset \left( {SBD} \right)\end{array} \right.\). \( \Rightarrow J\) là điểm chung thứ nhất của hai mặt phẳng \(\left( {AMN} \right)\) và \(\left( {SBD} \right)\). Trong \(\left( {ABCD} \right)\) gọi \(O = AC \cap BD\), suy ra \(SO \subset \left( {SAC} \right)\). Trong \(\left( {SAC} \right)\) gọi \(I = AM \cap SO\) ta có: \(\left\{ \begin{array}{l}I \in AM \subset \left( {AMN} \right)\\I \in SO \subset \left( {SBD} \right)\end{array} \right. \Rightarrow I\) là điểm chung thứ hai của hai mặt phẳng \(\left( {AMN} \right)\) và \(\left( {SBD} \right)\). \( \Rightarrow \left( {AMN} \right) \cap \left( {SBD} \right) = IJ\). Trong \(\left( {SBD} \right)\) gọi \(K = IJ \cap SD\). Vậy \(K = \left( {AMN} \right) \cap SD\). Chọn A Câu hỏi 42 : Cho hình chóp \(S.ABCD\) có \(O\) là giao điểm của hai đường chéo, \(M\) là một điểm trên cạnh \(SA\). Gọi \(I\) là giao điểm của \(MC\) và \(SO\). Giao điểm giữa \(SD\) và \(\left( {MBC} \right)\) là:
Đáp án: B Phương pháp giải: \(\left\{ \begin{array}{l}a \cap b = M\\b \subset \left( P \right)\end{array} \right. \Rightarrow a \cap \left( P \right) = M\). Lời giải chi tiết:
Ta có \(SD \subset \left( {SBD} \right)\) nên ta tìm giao tuyến của \(\left( {MBC} \right)\) và \(\left( {SBD} \right)\). Dễ thấy \(\left( {MBC} \right)\) và \(\left( {SBD} \right)\) có điểm chung thứ nhất là \(B\). Trong \(\left( {SAC} \right),\,\,MC \cap SO = I\). Ta có \(\left\{ \begin{array}{l}I \in MC \subset \left( {MBC} \right)\\I \in SO \subset \left( {SBD} \right)\end{array} \right. \Rightarrow I \in \left( {MBC} \right) \cap \left( {SBD} \right)\). \( \Rightarrow \left( {MBC} \right) \cap \left( {SBD} \right) = BI\). Trong \(\) gọi \(N = BI \cap SD \Rightarrow N = SD \cap \left( {MBC} \right)\). Chọn B Câu hỏi 43 : Cho hình chóp đều \(S.ABCD\) có tất cả các cạnh bằng \(a\), điểm \(M\) thuộc cạnh SC sao cho \(SM = 2MC\). Mặt phẳng \(\left( P \right)\) chứa \(AM\) và song song \(BD\). Tính diện tích của thiết diện của hình chóp \(S.ABCD\) bởi mặt phẳng \(\left( P \right)\).
Đáp án: C Phương pháp giải: - Tìm thiết diện của hình chóp dựa vào yếu tố song song. - Diện tích tứ giác có 2 đường chéo vuông góc bằng nửa tích hai đường chéo. Lời giải chi tiết:
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right).\) Trong \(\left( {SAC} \right)\), gọi \(SO \cap AM = G.\) Qua \(G\) kẻ đường thẳng song song \(BD\) cắt \(SB,\,\,SD\) lần lượt tại \(H,\,\,K\). Ta có: \( \Rightarrow \left( P \right) \cap \left( {SAC} \right) = HK\). Khi đó thiết diện cần tìm là tứ giác \(AHMK\). Ta có \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\)\( \Rightarrow BD \bot AM\) Do đó \(HK \bot AM\)\( \Rightarrow {S_{AHMK}} = \dfrac{{AM.HK}}{2}\) Ta có \(HK\parallel BD\)\( \Rightarrow \dfrac{{HK}}{{BD}} = \dfrac{{SG}}{{SO}}\) Áp dụng định lí Menelaus trong tam giác \(SOC\) có cát tuyến \(AGM\) ta có: \(\dfrac{{AC}}{{AO}}.\dfrac{{GO}}{{GS}}.\dfrac{{MS}}{{MC}} = 1\). Mà \(\dfrac{{AC}}{{AO}} = 2;\,\,\,\dfrac{{MS}}{{MC}} = 2\) \( \Rightarrow \dfrac{{GO}}{{GS}} = \dfrac{1}{4}\) \( \Rightarrow \dfrac{{SG}}{{SO}} = \dfrac{4}{5}\) \( \Rightarrow \dfrac{{HK}}{{BD}} = \dfrac{4}{5}\). Mà \(ABCD\) là hình vuông cạnh \(a\) nên \(AC = BD = a\sqrt 2 \)\( \Rightarrow HK = \dfrac{{4a\sqrt 2 }}{5}.\) Áp dụng định lí Menelaus trong tam giác \(AMC\) với cát tuyến là \(OGS\): \(\dfrac{{OA}}{{OC}}.\dfrac{{SC}}{{SM}}.\dfrac{{GM}}{{GA}} = 1\). Mà \(\dfrac{{OA}}{{OC}} = 1;\,\,\dfrac{{SC}}{{SM}} = \dfrac{3}{2}\)\( \Rightarrow \dfrac{{GM}}{{GA}} = \dfrac{2}{3} \Rightarrow \dfrac{{AG}}{{AM}} = \dfrac{3}{5}.\) Áp dụng định lí Pytago trong tam giác vuông \(SAO\) có: \(SO = \sqrt {S{A^2} - A{O^2}} \) \( = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{2}\). Vì \(\dfrac{{SG}}{{SO}} = \dfrac{4}{5} \Rightarrow \dfrac{{OG}}{{SO}} = \dfrac{1}{5}\)\( \Rightarrow OG = \dfrac{1}{5}SO = \dfrac{{a\sqrt 2 }}{{10}}\). Áp dụng định lí Pytago trong tam giác vuông \(AGO\) có: \(AG = \sqrt {G{O^2} + A{O^2}} \) \( = \sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{{10}}} \right)}^2}} = \dfrac{{a\sqrt {13} }}{5}\). Khi đó \(AM = \dfrac{5}{3}AG = \dfrac{{a\sqrt {13} }}{3}.\) +) \({S_{AHMK}} = \dfrac{{AM.HK}}{2} = \dfrac{1}{2}.\dfrac{{a\sqrt {13} }}{3}.\dfrac{{4a\sqrt 2 }}{5} = \dfrac{{2a\sqrt {26} }}{{15}}\) Chọn C. Câu hỏi 44 : Cho hình lập phương ABCD có cạnh là 2. Gọi M, N lần lượt là trung điểm của BC và CD. Tính diện tích thiết diện của hình lập phương khi cắt bởi mặt phẳng (A’MN).
Đáp án: A Phương pháp giải: \({S_{A'HMNK}} = \frac{{{S_{ABMND}}}}{{\cos \widehat {AIA'}}}\) Lời giải chi tiết:
Kéo dài MN cắt AB và AD lần lượt tại E và F. Gọi \(H = A'E \cap BB';\,\,K = A'F \cap DD'\). Khi đó thiết diện là A’HMNK. Ta có ABMND là hình chiếu của A’HMNK trên mặt phẳng \(\left( {ABCD} \right)\). Gọi \(I = AC \cap MN\) ta có: \(AC \bot BD;\,\,MN//BD \Rightarrow AC \bot MN\) tại I. \(\left\{ \begin{array}{l}MN \bot AI\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {A'AI} \right) \Rightarrow MN \bot A'I\) \( \Rightarrow \widehat {\left( {\left( {A'HMNK} \right);\left( {ABCD} \right)} \right)} = \widehat {AIA'}\) Ta có : \(CM = CN = 1 \Rightarrow MN = \sqrt 2 \Rightarrow IC = \frac{{\sqrt 2 }}{2}\) \(AC = 2\sqrt 2 \Rightarrow AI = 2\sqrt 2 - \frac{{\sqrt 2 }}{2} = \frac{{3\sqrt 2 }}{2}\). Xét tam giác vuông AA’I có: \(A'I = \sqrt {AA{'^2} + A{I^2}} = \sqrt {4 + \frac{9}{2}} = \frac{{\sqrt {34} }}{2}\). \( \Rightarrow \cos \widehat {AIA'} = \frac{{AI}}{{A'I}} = \frac{{\frac{{3\sqrt 2 }}{2}}}{{\frac{{\sqrt {34} }}{2}}} = \frac{3}{{\sqrt {17} }} = \cos \widehat {\left( {\left( {ABCD} \right);\left( {A'HMNK} \right)} \right)}\) Ta có \({S_{ABCD}} = 4;\,\,{S_{CMN}}\frac{1}{2}.1.1 = \frac{1}{2} \Rightarrow {S_{ABMND}} = 4 - \frac{1}{2} = \frac{7}{2}\) \( \Rightarrow {S_{A'HMNK}} = \frac{{{S_{ABMND}}}}{{\cos \widehat {AIA'}}} = \frac{7}{2}.\frac{{\sqrt {17} }}{3} = \frac{{7\sqrt {17} }}{6}\) . Chọn A. Câu hỏi 45 : Cho tứ diện \(ABCD\) có \(AB = BC = AC = CD = DB = a,\,\,AD = \dfrac{{a\sqrt 3 }}{2}\). Gọi \(M\) là trung điểm của \(AB\), điểm \(O\) là tâm đường tròn ngoại tiếp tam giác \(BCD\). Đường thẳng cắt mặt phẳng \(\left( {MCD} \right)\) tại \(G\). Tính diện tích tam giác \(GAD\).
Đáp án: B Phương pháp giải: Tính độ dài các đoạn \(GA,GD,AD\) rồi nhận xét tính chất tam giác \(GAD\). Lời giải chi tiết:
Tam giác \(ACD\) có \(AC = CD = a,AD = \dfrac{{a\sqrt 3 }}{2}\) nên \(A{E^2} = \dfrac{{A{C^2} + A{D^2}}}{2} - \dfrac{{C{D^2}}}{4}\)\( = \dfrac{{{a^2} + \dfrac{{3{a^2}}}{4}}}{2} - \dfrac{{{a^2}}}{4} = \dfrac{{5{a^2}}}{8}\) Tam giác \(BCD\) đều \( \Rightarrow BE = \dfrac{{a\sqrt 3 }}{2}\). Tam giác \(ABE\) có \(EM\) là đường trung tuyến của tam giác \(AEB\) nên : \(E{M^2} = \dfrac{{E{A^2} + E{B^2}}}{2} - \dfrac{{A{B^2}}}{4}\)\( = \dfrac{{\dfrac{{5{a^2}}}{8} + \dfrac{{3{a^2}}}{4}}}{2} - \dfrac{{{a^2}}}{4} = \dfrac{{7{a^2}}}{{16}}\) Xét tam giác \(BME\) và bộ ba điểm \(A,G,O\) thẳng hàng có : \(\dfrac{{AM}}{{AB}}.\dfrac{{OB}}{{OE}}.\dfrac{{GE}}{{GM}} = 1\)\( \Rightarrow \dfrac{1}{2}.2.\dfrac{{GE}}{{GM}} = 1 \Leftrightarrow \dfrac{{GE}}{{GM}} = 1\) hay \(G\) là trung điểm của \(ME\). Xét tam giác \(ABD\) có \(DM\) là trung tuyến của \(\Delta ABD\) nên \(D{M^2} = \dfrac{{D{A^2} + B{D^2}}}{2} - \dfrac{{A{B^2}}}{4} = \dfrac{{5{a^2}}}{8}\). Tam giác \(DME\) có trung tuyến \(DG\) nên \(D{G^2} = \dfrac{{D{E^2} + D{M^2}}}{2} - \dfrac{{M{E^2}}}{4}\)\( = \dfrac{{\dfrac{{{a^2}}}{4} + \dfrac{{5{a^2}}}{8}}}{2} - \dfrac{{7{a^2}}}{{64}} = \dfrac{{21{a^2}}}{{64}}\). Lại có \(\cos \widehat {AEM} = \dfrac{{A{E^2} + E{M^2} - A{M^2}}}{{2AE.EM}}\)\( = \dfrac{{\dfrac{{5{a^2}}}{8} + \dfrac{{7{a^2}}}{{16}} - \dfrac{{{a^2}}}{4}}}{{2.\sqrt {\dfrac{{5{a^2}}}{8}.\dfrac{{7{a^2}}}{{16}}} }} = \dfrac{{13}}{{2\sqrt {70} }}\) \( \Rightarrow A{G^2} = A{E^2} + E{G^2} - 2AE.EG\cos \widehat {AEG}\)\( = \dfrac{{5{a^2}}}{8} + \dfrac{{7{a^2}}}{{64}} - 2.\sqrt {\dfrac{{5{a^2}}}{8}.\dfrac{{7{a^2}}}{{64}}} .\dfrac{{13}}{{2\sqrt {70} }}\)\( = \dfrac{{21{a^2}}}{{64}}\) Tam giác \(ADG\) có \(A{G^2} = \dfrac{{21{a^2}}}{{64}},A{D^2} = \dfrac{{3{a^2}}}{4},D{G^2} = \dfrac{{21{a^2}}}{{64}}\) Do đó \(\Delta GAD\) cân tại \(G\). Gọi \(H\) là trung điểm của \(AD\) thì \(AH = \dfrac{{a\sqrt 3 }}{4},\) \(G{H^2} = G{A^2} - A{H^2}\)\( = \dfrac{{21{a^2}}}{{64}} - \dfrac{{3{a^2}}}{{16}} = \dfrac{{9{a^2}}}{{64}}\)\( \Rightarrow GH = \dfrac{{3a}}{8}\) Diện tích tam giác \({S_{GAD}} = \dfrac{1}{2}GH.AD\)\( = \dfrac{1}{2}.\dfrac{{3a}}{8}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{3{a^2}\sqrt 3 }}{{32}}\) Chọn B. Câu hỏi 46 : Cho tứ diện ABCD có M, N lần lượt là trung điểm AC, BC. K là điểm thuộc cạnh BD sao cho BK = 2KD. Gọi I là giao điểm của AD và (MNK). MI cắt CD tại điểm E. Khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: Phương pháp: Ta tìm giao tuyến của đường thẳng b và mặt phẳng (α): + Tìm một mặt phẳng chứa b thích hợp + Tìm giao tuyến của mặt phẳng này với mặt phẳng (α) + Tìm giao điểm của giao tuyến đó với đường thẳng b Lời giải chi tiết:
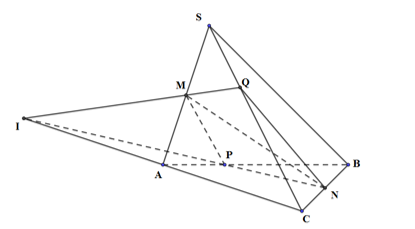
Vì I là giao của AD và (MNK) nên I ∈ (MNK) ⇒ MI ⊂ (MNK) Mà E ∈ MI ⇒ E ∈ (MNK) ⇒ E thuộc giao tuyến của (MNK) và (BCD) ⇒ E ∈ NK Chọn đáp án C Câu hỏi 47 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,\,\,P\) lần lượt là trung điểm của các cạnh \(SA\) và \(SC.\) Điểm \(N\) thuộc cạnh \(SB\) sao cho \(\frac{SN}{SB}=\frac{2}{3}.\) Gọi \(Q\) là giao điểm của cạnh \(SD\) và mặt phẳng \(\left( MNP \right).\) Tính tỉ số \(\frac{SQ}{SD}.\)
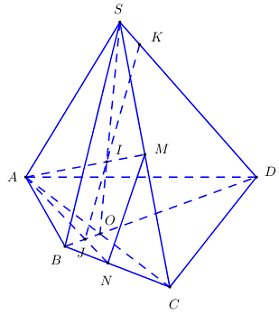
Đáp án: A Phương pháp giải: Xác định điểm Q trên SD sau đó tính tỉ số cần tính nhờ định lí Menelaus : Cho tam giác ABC, các điểm D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó D, E, F thẳng hàng khi và chỉ khi \(\frac{FA}{FB}.\frac{DB}{DC}.\frac{EC}{EA}=1\). Lời giải chi tiết: Gọi O là tâm hình bình hành ABCD. Gọi I là giao điểm của SO và MP. Trong mặt phẳng (SBD), kéo dài NI cắt SD tại Q, cắt BD tại E. Áp dụng định lí Menelaus trong tam giác SOB ta có : \(\frac{MS}{MO}.\frac{EO}{EB}.\frac{NB}{NS}=1\Leftrightarrow 1.\frac{EO}{EB}.\frac{1}{2}=1\Rightarrow \frac{EO}{EB}=2\) \(\Rightarrow \frac{ED}{EB}=3\) Áp dụng định lí Menelaus trong tam giác SBD ta có : \(\frac{QS}{QD}.\frac{ED}{EB}.\frac{NB}{NS}=1\Leftrightarrow \frac{QS}{QD}.3.\frac{1}{2}=1\Leftrightarrow \frac{QS}{QD}=\frac{2}{3}\) \(\Rightarrow \frac{SQ}{SD}=\frac{2}{5}\) Chọn A. Câu hỏi 48 : Cho hình chóp \(SABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O.\) Gọi \(M,N,P\) lần lượt là trung điểm \(BC,CD,SO.\) Tìm giao tuyến của \(\left( {MNP} \right)\) với các mặt phẳng \(\left( {ABCD} \right),\left( {SAB} \right),\left( {SAD} \right),\left( {SBC} \right),\left( {SCD} \right).\) Phương pháp giải: Lời giải chi tiết:
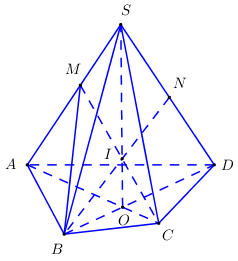
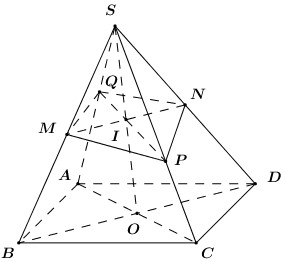
+ Tìm \(\left( {MNP} \right) \cap \left( {ABCD} \right)\). Ta có \(\begin{array}{l}M \in \left( {MNP} \right);\,\,M \in BC \subset \left( {ABCD} \right) \Rightarrow M \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\N \in \left( {MNP} \right);\,\,N \in CD \subset \left( {ABCD} \right) \Rightarrow N \in \left( {MNP} \right) \cap \left( {ABCD} \right)\end{array}\) Vậy \(\left( {MNP} \right) \cap \left( {ABCD} \right) = MN\). + Tìm \(\left( {MNP} \right) \cap \left( {SAB} \right)\). Trong \(\left( {ABCD} \right)\) gọi \(E = MN \cap AB\). Gọi \(I = MN \cap AC \Rightarrow I \in AC \Rightarrow I \in \left( {SAC} \right)\). Lại có : \(P \in SO \Rightarrow P \in \left( {SAC} \right)\). Trong \(\left( {SAC} \right)\) gọi \(F = PI \cap SA\) ta có : \(\begin{array}{l}E \in MN \subset \left( {MNP} \right) \Rightarrow E \in \left( {MNP} \right);\,\,E \in AB \subset \left( {SAB} \right) \Rightarrow E \in \left( {SAB} \right) \Rightarrow E \in \left( {MNP} \right) \cap \left( {SAB} \right)\\F \in PI \subset \left( {MNP} \right) \Rightarrow F \in \left( {MNP} \right);\,\,F \in SA \subset \left( {SAB} \right) \Rightarrow F \in \left( {SAB} \right) \Rightarrow F \in \left( {MNP} \right) \cap \left( {SAB} \right)\end{array}\) Vậy \(\left( {MNP} \right) \cap \left( {SAB} \right) = EF\). + Tìm \(\left( {MNP} \right) \cap \left( {SAD} \right)\). Trong \(\left( {ABCD} \right)\) gọi \(G = M \cap AD\). Ta có : \(\begin{array}{l}G \in MN \subset \left( {MNP} \right) \Rightarrow G \in \left( {MNP} \right);\,\,G \in AD \subset \left( {SAD} \right) \Rightarrow G \in \left( {SAD} \right) \Rightarrow G \in \left( {MNP} \right) \cap \left( {SAD} \right)\\F \in PI \subset \left( {MNP} \right) \Rightarrow F \in \left( {MNP} \right);\,\,F \in SA \subset \left( {SAD} \right) \Rightarrow F \in \left( {SAD} \right) \Rightarrow F \in \left( {MNP} \right) \cap \left( {SAD} \right)\end{array}\) Vậy \(\left( {MNP} \right) \cap \left( {SAD} \right) = FG\). + Tìm \(\left( {MNP} \right) \cap \left( {SBC} \right)\). M là điểm chung thứ nhất. Trong \(\left( {SAB} \right)\) gọi \(H = EF \cap SB\) ta có : \(H \in EF \subset \left( {MNP} \right) \Rightarrow H \in \left( {MNP} \right),\,\,H \in SB \subset \left( {SBC} \right) \Rightarrow H \in \left( {SBC} \right)\) \( \Rightarrow H \in \left( {MNP} \right) \cap \left( {SBC} \right) \Rightarrow H\) là điểm chung thứ hai. Vậy \(\left( {MNP} \right) \cap \left( {SBC} \right) = MH\). + Tìm \(\left( {MNP} \right) \cap \left( {SCD} \right)\). N là điểm chung thứ nhất. Trong \(\left( {SAD} \right)\) gọi \(K = FG \cap SD\) ta có : \(K \in FG \subset \left( {MNP} \right) \Rightarrow K \in \left( {MNP} \right);\,\,K \in SD \subset \left( {SCD} \right) \Rightarrow K \in \left( {SCD} \right)\). \( \Rightarrow K \in \left( {MNP} \right) \cap \left( {SCD} \right) \Rightarrow K\) là điểm chung thứ hai. Vậy \(\left( {MNP} \right) \cap \left( {SCD} \right) = NK\). Câu hỏi 49 : Cho hình chóp \(SABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,N\) lần lượt là trung điểm \(SB,SD\) và \(P \in SC\) sao cho \(SP > PC.\) Tìm giao tuyến của \(\left( {MNP} \right)\) với các mặt phẳng \(\left( {SAC} \right),\left( {SAB} \right),\left( {SAD} \right).\) Phương pháp giải: Lời giải chi tiết:
* Tìm \(\left( {MNP} \right) \cap \left( {SAC} \right)\). + P là điểm chung thứ nhất. + Trong \(\left( {ABCD} \right)\) gọi \(O = AC \cap BD\), trong \(\left( {SBD} \right)\) gọi \(I = MN \cap SO\) ta có : \(\left\{ \begin{array}{l}I \in MN \subset \left( {MNP} \right) \Rightarrow I \in \left( {MNP} \right)\\I \in SO \subset \left( {SAC} \right) \Rightarrow I \in \left( {SAC} \right)\end{array} \right. \Rightarrow I \in \left( {MNP} \right) \cap \left( {SAC} \right)\). \( \Rightarrow I\) là điểm chung thứ hai. Vậy \(PI = \left( {MNP} \right) \cap \left( {SAC} \right)\). * Tìm \(\left( {MNP} \right) \cap \left( {SAB} \right)\). + M là điểm chung thứ nhất. Trong \(\left( {SAC} \right)\) gọi \(Q = IP \cap SA\) ta có : \(\left\{ \begin{array}{l}Q \in IP \subset \left( {MNP} \right) \Rightarrow Q \in \left( {MNP} \right)\\Q \in SA \subset \left( {SAB} \right) \Rightarrow Q \in \left( {SAB} \right)\end{array} \right. \Rightarrow Q \in \left( {MNP} \right) \cap \left( {SAB} \right)\). \( \Rightarrow Q\) là điểm chung thứ hai. Vậy \(\left( {MNP} \right) \cap \left( {SAB} \right) = MQ\). * Tìm \(\left( {MNP} \right) \cap \left( {SAD} \right)\). + N là điểm chung thứ nhất. + Q là điểm chung thứ hai. Vậy \(\left( {MNP} \right) \cap \left( {SAD} \right) = NQ\). Câu hỏi 50 : Cho \(\Delta ABC\) và một điểm \(S\) không thuộc mặt phẳng \(\left( {ABC} \right).\) Gọi \(M,N\) lần lượt là trung điểm \(AB,BC.\) Tìm giao tuyến của hai mặt phẳng \(\left( {SAN} \right)\) và \(\left( {SMC} \right).\) Phương pháp giải: Lời giải chi tiết:
Trong \(\left( {ABCD} \right)\) gọi \(I = AN \cap CM\) ta có: \(\left\{ \begin{array}{l}I \in AN \subset \left( {SAN} \right) \Rightarrow I \in \left( {SAN} \right)\\I \in CM \subset \left( {SCM} \right) \Rightarrow I \in \left( {SCM} \right)\end{array} \right. \Rightarrow I \in \left( {SAN} \right) \cap \left( {SCM} \right)\). Xét \(\left( {SAN} \right)\) và \(\left( {SCM} \right)\) có: + S là điểm chung thứ nhất. + I là điểm chung thứ hai. Vậy \(\left( {SAN} \right) \cap \left( {SCM} \right) = SI\).
|