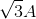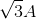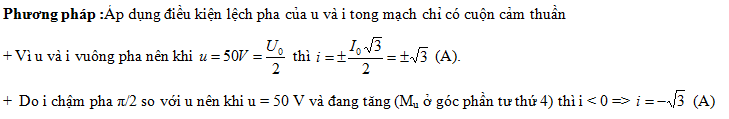50 bài tập Các mạch điện xoay chiều mức độ vận dụng (Phần 1)Làm bàiCâu hỏi 1 : Dòng điện có cường độ 2A chạy qua một vật dẫn có điện trở 200Ω. Nhiệt lượng tỏa ra trên vật dẫn đố trong 40s là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C Nhiệt lượng toả ra :\(Q = {I^2}Rt = {2^2}.200.40 = 32000J = 32kJ\) Câu hỏi 2 : Đặt điện áp \(u = 100\sqrt 2 \cos 100\pi t\,\left( {\rm{V}} \right)\) vào hai đầu một điện trở thuần 50 Ω. Công suất tiêu thụ của điện trở bằng
Đáp án: C Phương pháp giải: Áp dụng công thức tính công suất điện \(P = {{{U^2}} \over R}\) Lời giải chi tiết: Đáp án C + Công suất tiêu thụ của điện trở \(P = {{{U^2}} \over R} = {{{{100}^2}} \over {50}} = 200W\) Câu hỏi 3 : Đặt điện áp xoay chiều có giá trị cực đại là 100 V vào hai đầu một cuộn cảm thuần thì cường độ dòng điện trong cuộn cảm có biểu thức
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 4 : Hãy sắp xếp giá trị dung kháng của tụ điện theo thứ tự tăng dần, khi tần số của dòng điện qua tụ có giá trị lần lượt là \({f_1} = 10Hz;{f_2} = 8Hz;{f_3} = 12Hz;{f_4} = 20Hz\)
Đáp án: D Phương pháp giải: sử dụng công thức tính dung kháng Lời giải chi tiết: Dung kháng của tụ: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}}\) Suy ra dung kháng tỉ lệ nghịch với tần số Mà : \({f_4} > {f_3} > {f_1} > {f_2} \Rightarrow {Z_{C4}} < {Z_{C3}} < {Z_{C1}} < {Z_{C2}}\) Câu hỏi 5 : Đặt vào hai đầu cuộn cảm thuần có độ tự cảm L = 0,5 H một hiệu điện thế xoay chiều thì biểu thức từ thông riêng trong cuộn cảm là Φ = 2cos100t Wb, t tính bằng s. Giá trị hiệu điện thế hiệu dụng hai đầu cuộn cảm là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A. + Từ thông riêng của mạch \(\Phi = {\rm{Li}} \to {{\rm{I}}_0} = {{{\Phi _0}} \over {\rm{L}}} = {2 \over {0,5}} = 4{\rm{A}}{\rm{.}}\) Điện áp hiệu dụng hai đầu cuộn cảm \({\rm{U = I}}{{\rm{Z}}_{\rm{L}}} = 2\sqrt 2 .\left( {0,5.100} \right) = 100\sqrt 2 {\rm{V}}{\rm{.}}\) Câu hỏi 6 : Một tụ điện có điện dung không đổi khi mắc vào mạng điện 110V – 60Hz thì cường độ dòng điện hiệu dụng trong mạch là 1,5A. Khi mắc tụ điện đó vào mạng điện 220V – 50Hz thì cường độ dòng điện hiệu dụng trong mạch là
Đáp án: B Phương pháp giải: Cường độ dòng điện hiệu dụng I = U/ZC Lời giải chi tiết: - Khi mắc vào mạng điện 110V - 60Hz thì I1 = 1,5A Ta có: \({I_1} = {{{U_1}} \over {{Z_{{C_1}}}}} \to {Z_{{C_1}}} = {{{U_1}} \over {{I_1}}} = {{110} \over {1,5}} = {{220} \over 3}\Omega \) Mặt khác, ta có: \({Z_C}_1 = {1 \over {{\omega _1}C}} \to C = {1 \over {{Z_{{C_1}}}{\omega _1}}} = {1 \over {{Z_{{C_1}}}2\pi {f_1}}} = {1 \over {{{220} \over 3}2\pi .60}} = {1 \over {8800\pi }}\) - Khi mắc vào mạng điện 220 - 50Hz: \({Z_{{C_2}}} = {1 \over {{\omega _2}C}} = {1 \over {2\pi {f_2}C}} = {1 \over {2\pi .50.{1 \over {8800\pi }}}} = 88\Omega \Rightarrow {I_2} = {{{U_2}} \over {{Z_{{C_2}}}}} = {{220} \over {88}} = 2,5A\) Chọn B Câu hỏi 7 : Đặt điện áp xoay chiều \(u = {U_0}\cos \left( {100\pi t + \pi /3} \right)\)vào hai đầu một cuộn cảm thuần có độ tự cảm \(L = 1/2\pi \;H\). Ở thời điểm điện áp ở hai đầu cuộn cảm là \(100\sqrt 2 V\) thì cường độ dòng điện qua cuộn cảm là 2A. Biểu thức của cường độ dòng điện qua cuộn cảm :
Đáp án: C Phương pháp giải: Mạch điện chỉ có cuộn cảm thuần: u sớm pha hơn i góc π/2 Sử dụng hệ thức vuông pha giữa u và i Lời giải chi tiết: + Dung kháng: \({Z_L} = 100\pi .{1 \over {2\pi }} = 50\Omega \) + Sử dụng hệ thức vuông pha giữa u và i: \({{{i^2}} \over {I_0^2}} + {{{u^2}} \over {U_0^2}} = 1 \Leftrightarrow {{{2^2}} \over {I_0^2}} + {{{{\left( {100\sqrt 2 } \right)}^2}} \over {{{50}^2}.I_0^2}} = 1 \Rightarrow {I_0} = 2\sqrt 3 A\) + i trễ pha hơn u góc π/2 => φi = -π/6 => Phương trình của i: \(i = 2\sqrt 3 c{\rm{os}}\left( {100\pi t - {\pi \over 6}} \right)A\) Câu hỏi 8 : Đặt một điện áp xoay chiều có \(u = 120\sqrt 2 \cos 100\pi t\,V\) vào hai đầu một mạch điện gồm một điện trở R nối tiếp với một bóng đèn 100 V – 100 W. Muốn đèn sáng bình thường thì R có giá trị là bao nhiêu?
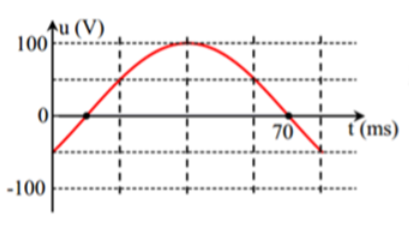
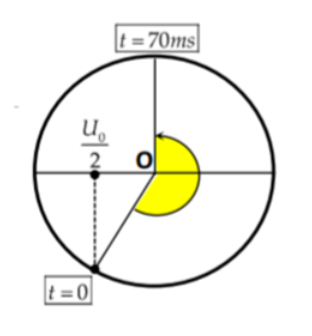
Đáp án: A Phương pháp giải: Lời giải chi tiết: Chọn đáp án A + Dòng điện chạy trong mạch khi đèn sáng bình thường\(I = \frac{{{P_d}}}{{{U_d}}} = \frac{{100}}{{100}} = 1\,\,{\rm{A}}{\rm{.}}\) \( \to \) Điện ap hiệu dụng ở hai đầu điện trở \({U_R} = U - {U_d} = 20\,\,V.\) \( \to \)Giá trị của R là\({\rm{R}} = \frac{{{U_R}}}{I} = \frac{{20}}{I} = 20\,\,\Omega .\) Câu hỏi 9 : Đặt điện áp xoay chiều vào hai bản tụ điện có dung kháng là ZC = 50Ω. Điện áp giữa hai bản tụ điện được mô tả như hình bên. Biểu thức cường độ dòng điện qua tụ là
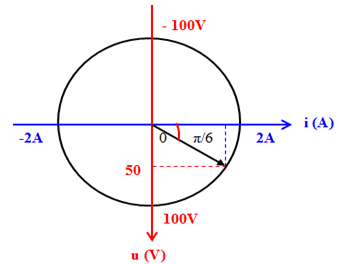
Đáp án: A Phương pháp giải: Áp dụng vòng tròn lượng giác trong dòng điện xoay chiều Lời giải chi tiết: Đáp án A Từ đồ thị ta có \(\frac{T}{2} + \frac{T}{{12}} = {70.10^{ - 3}}s = > T = 0,12s = > \omega = \frac{{50\pi }}{3}\) \(\left\{ \begin{array}{l}{\varphi _u} = - \frac{{2\pi }}{3}\\{U_0} = 100V\end{array} \right. = > \left\{ \begin{array}{l}{\varphi _i} = {\varphi _u} + \frac{\pi }{2} = - \frac{\pi }{6}\\{I_0} = \frac{{{U_0}}}{{{Z_C}}} = \frac{{100}}{{50}} = 2A\end{array} \right. = > i = 2\cos \left( {\frac{{50\pi t}}{3} - \frac{\pi }{6}} \right)(A)\) Câu hỏi 10 : Đặt điện áp \(u = {U_0}\cos (\omega t + \frac{\pi }{4})\)vào hai đầu đoạn mạch chỉ có tụ điện thì cường độ dòng điện trong mạch là \(i = {I_0}\cos (\omega t + {\varphi _i})\). Giá trị của φi bằng
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đáp án C Do mạch chỉ chứ tụ điện nên điện áp chậm pha hơn cường độ dòng điện trong mạch một góc \(\frac{\pi }{2}\). Giá trị của φi bằng \(\frac{{3\pi }}{4}\) Câu hỏi 11 : Phát biểu định luật Ôm cho mạch điện xoay chiều chỉ có, a) một tụ điện; b) một cuộn cảm thuần. Phương pháp giải: Lời giải chi tiết: Định luật Ôm của dòng điện xoay chiều chỉ có một tụ điện. Cường độ hiệu dụng trong mạch chứa tụ điện có giá trị bằng thương số của điện áp hiệu dụng giữa hai đầu mạch và dung kháng của mạch. Định luật Ôm của dòng điện xoay chiều chỉ có một cuộn cảm thuần. Cường độ hiệu dụng trong mạch chứa một cuộn cảm thuần có giá trị bằng thương số của điện áp hiệu dụng giữa hai đầu mạch và cảm kháng của mạch. Câu hỏi 12 : Dựa vào định luật Ôm, hãy so sánh tác dụng cản trở dòng điện xoay chiều thể hiện trong. a) ZC; b) ZL .
. Phương pháp giải: Lời giải chi tiết: Từ \({Z_L} = \omega L;{Z_C} = \frac{1}{{\omega C}}\) ta có các nhận xét sau ZC tỷ lệ nghịch với C và f Nếu C và f tăng thì ZC giảm, ít cản trở dòng điện và ngược lại. Cảm kháng ZL = Lω = 2πf.L ; ZL tỉ lệ với L và f Nếu L và f tăng thì cản trở dòng điện nhiều và ngược lại Câu hỏi 13 : Chứng minh rằng, khi hai cuộn cảm thuần L1 và L2 mắc nối tiếp trong một mạch điện xoay chiều thì cuộn cảm tương đương có cảm kháng cho bởi: ZL = (L1 + L2) ω Phương pháp giải: + Mạch có L1 và L2 mắc nối tiếp thì: u = u1 + u2 + Dung kháng: ZL = ωL Lời giải chi tiết: Khi L1 và L2 mắc nối tiếp thì: \(\begin{array}{l}u = {u_1} + {u_2} = - {L_1}\frac{{di}}{{dt}} - {L_2}\frac{{di}}{{dt}}\\u = - \left( {{L_1} + {L_2}} \right)\frac{{di}}{{dt}} = - L\frac{{di}}{{dt}}\end{array}\) Với L = L1 + L2 => Cảm kháng: \({Z_L} = \omega L = {L_1}\omega + {L_2}\omega = {Z_{L1}} + {Z_{L2}} = \left( {{L_1} + {L_2}} \right)\omega {\rm{ }}\) Câu hỏi 14 : Dòng điện xoay chiều có cường độ hiệu dụng 2 A chạy qua điện trở 110 Ω. Công suất tỏa nhiệt trên điện trở bằng
Đáp án: B Phương pháp giải: Áp dụng công thức tính công suất tỏa nhiệt P=RI2 Lời giải chi tiết: Đáp án B Áp dụng công thức tính công suất tỏa nhiệt P = RI2 = 440W Câu hỏi 15 : Đặt điện áp xoay chiều vào hai đầu đoạn mạch chỉ có điện trở thuần R = 10 Ω thì trong mạch xuất hiện dòng điện xoay chiều. Biết nhiệt lượng tỏa ra trong 30 phút là 900 kJ. Cường độ dòng điện cực đại trong mạch là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Chọn A + Nhiệt lượng tỏa ra trên điện trở \(Q = {I^2}Rt = 0,5{I_0}Rt \to {I_0} = 10\,\,A.\) Câu hỏi 16 : Đặt điện áp \(u = {U_0}\cos \left( {100\pi t + \frac{\pi }{3}} \right)\,\left( V \right)\) vào hai đầu một cuộn cảm thuần có độ tự cảm \(L = \frac{1}{{2\pi }}H\). Ở thời điểm điện áp giữa hai đầu cuộn ảm là \(100\sqrt 2 \)V thì cường độ dòng điện qua cuộn cảm là 2A. Biểu thức của cường độ dòng điện qua cuộn cảm này là
Đáp án: C Phương pháp giải: Lời giải chi tiết: + Cảm kháng của cuộn dây \({Z_L} = L\omega = 50\Omega \). \( \to \) Đoạn mạch chỉ chứa cuộn dây thì điện áp luôn sớm pha so với dòng điện một góc \(0,5\pi \). + Ta có: \({\left( {\frac{u}{{{U_0}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1 \Leftrightarrow {\left( {\frac{{100\sqrt 2 }}{{50{I_0}}}} \right)^2} + {\left( {\frac{2}{{{I_0}}}} \right)^2} = 1 \Rightarrow {I_0} = 2\sqrt 3 A.\) \( \to i = 2\sqrt 3 \cos \left( {100\pi t - \frac{\pi }{6}} \right)A\) à Chọn C Câu hỏi 17 : Cho đoạn mạch điện xoay chiều chỉ có tụ điện với điện dung C. Tại thời điểm t1 điện áp và dòng điện qua tụ điện có giá trị lần lượt là 40V; 1A. Tại thời điểm t2 điện áp và dòng điện qua tụ điện có giá trị lần lượt là 50V; 0,6A. Dung kháng của mạch có giá trị là
Đáp án: A Phương pháp giải: Sử dụng công thức liên hệ giữa hai đại lượng vuông pha Lời giải chi tiết: ta có
Câu hỏi 18 : Một dây đồng dài 48m, bên ngoài phủ một lớp sơn cách điện mỏng. Sợi dây được quấn thành một ống dây dài 50 cm, đường kính 3cm, cho các vòng dây quấn sát nhau. Cho dòng điện \(i = 2\sqrt 2 \cos (100\pi t)(A)\) chạy qua ống dây. Tính cảm kháng của ống dây?
Đáp án: C Phương pháp giải: Sử dụng công thức tính độ tự cảm của ống dây và công thức tính cảm kháng Lời giải chi tiết: số vòng dây quấn được là: \(N = \frac{{48}}{{\pi d}} = \frac{{48}}{{\pi .0,03}} = 509vong\) công thức tính độ tự cảm là \(L = 4\pi {.10^{ - 7}}.\frac{{{N^2}}}{l}.S = 4\pi {.10^{ - 7}}.\frac{{{{509}^2}}}{{0,5}}.(\pi 0,{015^2}) = 4,{6.10^{ - 4}}H\) Cảm kháng của cuộn dây là \({Z_L} = \omega .L = 100\pi .4,{6.10^{ - 4}} = 0,145\Omega \) Câu hỏi 19 : Đặt một điện áp xoay chiều \(u = {U_0}.\cos \left( {100\pi t + \frac{{2\pi }}{3}} \right)(V)\) vào hai đầu một cuộn cảm thuần có độ tự cảm \(L = \frac{1}{{2,5\pi }}H\). Ở thời điểm điện áp giữa hai đầu cuộn cảm là 160 V thì cường độ dòng điện trong mạch là 3A. Biểu thức của cường độ dòng điện trong mạch là
Đáp án: C Phương pháp giải: Áp dụng công thức độc lập với thời gian của hai đại lượng vuông pha Lời giải chi tiết: Vì đoạn mạch chỉ chứa cuộn cảm thuần nên cường độ dòng điện trễ pha π/2 so với điện áp. Cảm kháng của cuộn dây là: \({Z_L} = \omega .L = 100\pi .\frac{1}{{2,5\pi }} = 40\Omega \) Áp dụng công thức với hai đại lượng vuông pha ta có:
Câu hỏi 20 : Nếu đặt vào hai đâù một tụ điện có điện dung \(C = \frac{{{{2.10}^{ - 4}}}}{\pi }(F)\) một điện áp xoay chiều thì cường độ dòng điện hiệu dụng chạy qua mạch bằng \(u = 200\sqrt 2 \cos \left( {100\pi t - \frac{\pi }{4}} \right)(V)\)
Đáp án: A Phương pháp giải: Áp dụng định luật Ôm cho đoạn mạch chỉ chứa tụ điện Lời giải chi tiết: Dung kháng của tụ là : \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{1}{\pi }{{2.10}^{ - 4}}}} = 50\Omega \) Cường độ dòng điện hiệu dụng là \(I = \frac{U}{{{Z_C}}} = \frac{{200}}{{50}} = 4A\) Câu hỏi 21 : Đặt vào hai đầu một cuộn dây thuần cảm một hiệu điện thế xoay chiều có giá trị hiệu dụng U không đổi và tần số f thay đổi. Khi f = 50Hz thì cường độ hiệu dụng qua cuộn dây là 2A. Để cường độ hiệu dụng qua cuộn dây bằng 4A thì tần số của dòng điện phải bằng bao nhiêu?
Đáp án: A Phương pháp giải: Biểu thức định luật Ôm cho đoạn mạch chỉ chứa cuộn cảm thuần \(I = \frac{U}{{{Z_L}}} = \frac{U}{{\omega L}}\) Lời giải chi tiết: Áp dụng định luật Ôm cho đoạn mạch chỉ chứa cuộn cảm : \(\left\{ \begin{array}{l}I = \frac{U}{{{\omega _1}L}} = \frac{U}{{2\pi {f_1}L}} = 2A\\I' = \frac{U}{{{\omega _2}L}} = \frac{U}{{2\pi {f_2}L}} = 4A\end{array} \right. \Rightarrow \frac{{I'}}{I} = \frac{{{f_1}}}{{{f_2}}} = 2 \Rightarrow {f_2} = 25Hz\) Câu hỏi 22 : Mạch điện X chỉ có một một điện trở thuần R có biểu thức dòng điện và điện áp lần lượt :\(i=2\sqrt{2}\text{cos(100}\pi \text{t+}\frac{\pi }{6})A\) và \(u=200\sqrt{2}\text{cos(100}\pi \text{t+}\frac{\pi }{6})A\). Hãy xác định giá trị điện trở thuần R đó?
Đáp án: A Phương pháp giải: Định luật Ôm cho đoạn mạch: U = IR Liên hệ giữa giá trị hiệu dụng và cực đại: \(U=\frac{{{U}_{0}}}{\sqrt{2}};I=\frac{{{I}_{0}}}{\sqrt{2}}\) Lời giải chi tiết: Điện trở thuần R của mạch: \(R=\frac{U}{I}=\frac{{{U}_{0}}}{{{I}_{0}}}=\frac{200\sqrt{2}}{2\sqrt{2}}=100\Omega \) Câu hỏi 23 : Mạch điện xoay chiều chỉ có một trong ba phần tử là điện trở thuần, tụ điện hoặc cuộn dây. Biết điện áp hai đầu đoạn mạch và cường độ dòng điện tức thời có biểu thức u = U0cos100πt (V) và i = I0cos(100πt – π/2) (A). Phần tử của mạch điện này là
Đáp án: A Phương pháp giải: Mạch điện chỉ chứa cuộn cảm thuần có dòng điện chậm pha hơn điện áp π/2 Lời giải chi tiết: Vì i trễ pha hơn u π/2 nên đoạn mạch chỉ chứa cuộn dây thuần cảm. Chọn A Câu hỏi 24 : Cường độ dòng điện chạy qua một đoạn mạch chỉ có tụ điện có biểu thức:
Đáp án: A Phương pháp giải: Áp dụng công thức tính dung kháng \({Z_C} = \frac{1}{{\omega C}}\) Lời giải chi tiết: Dung kháng : \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{10{}^{ - 4}}}{{2\pi }}}} = 200\Omega \) Câu hỏi 25 : Đặt điện áp xoay chiều u = U0cosωt vào hai đầu đoạn mạch chỉ có điện trở thuần. Gọi U là điện áp hiệu dụng giữa hai đầu đoạn mạch, i, I0 và I lần lượt là giá trị tức thời, giá trị cực đại và giá trị hiệu dụng của cường độ dòng điện trong đoạn mạch. Hệ thức nào sau đây sai?
Đáp án: C Phương pháp giải: Mạch chỉ có điện trở thuần nên u và i cùng pha. Định luật Ôm cho đoạn mạch chỉ chứa R là I = U/R Lời giải chi tiết: Với mạch chỉ có R, gọi u = U0cosφ là điện áp đặt vào hai đầu mạch thì cường độ dòng điện qua mạch là i = I0cosφ \(\frac{{{u}^{2}}}{U_{0}^{2}}+\frac{{{i}^{2}}}{I_{0}^{2}}=2{{\cos }^{2}}\varphi \ne 1\) Chọn C Câu hỏi 26 : Đặt điện áp u = 100\(\sqrt{2}\) cos(100πt + π/6) (V) vào hai đầu đoạn mạch chỉ có cuộn cảm thuần. Thời gian ngắn nhất giữa hai lần mà từ thông gửi qua cuộn cảm có độ lớn \(\frac{\sqrt{2}}{2\pi }\) Wb là
Đáp án: B Phương pháp giải: Cường độ dòng điện chậm pha π/2 so với điện áp giữa hai đầu đoạn mạch chỉ có cuộn cảm thuần. Từ thông qua cuộn cảm là φ = Li Cảm kháng ZL = ωL Định luật Ôm cho đoạn mạch : I = U/Z Lời giải chi tiết: Biểu thức dòng điện qua mạch: \(i=\frac{100\sqrt{2}}{{{Z}_{L}}}\text{cos(100}\pi \text{t-}\frac{\pi }{3})(A)\) Biểu thức từ thông qua cuộn cảm: \(\varphi =Li=L\frac{100\sqrt{2}}{\omega L}\text{cos(100}\pi \text{t-}\frac{\pi }{3})=\frac{\sqrt{2}}{\pi }\text{cos(100}\pi \text{t-}\frac{\pi }{3})\) Thời gian giữa hai lần ngắn nhất từ thông có độ lớn = 0,5φ0 là T/6 = 1/300 (s) Chọn B Câu hỏi 27 : Một mạch dao động LC lí tưởng gồm cuộn cảm thuần có độ tự cảm không đổi, tụ điện có điện dung C thay đổi. Khi C = C1 thì tần số dao động riêng của mạch là 6MHz và khi C = C2 thì tần số dao động riêng của mạch là 8MHz. Nếu C = 2C1 + 3C2 thì tần số dao động riêng của mạch là
Đáp án: A Phương pháp giải: Tần số dao động riêng của mạch LC là \(f=\frac{1}{2\pi \sqrt{LC}}\) Lời giải chi tiết: Tần số dao động riêng của mạch LC là \(f=\frac{1}{2\pi \sqrt{LC}}\) Khi C = C1 thì \({{f}_{1}}=\frac{1}{2\pi \sqrt{L{{C}_{1}}}}={{6.10}^{6}}Hz\) (1) Khi C = C2 thì \({{f}_{2}}=\frac{1}{2\pi \sqrt{L{{C}_{2}}}}={{8.10}^{6}}Hz\) (2) Khi C = 2C1 + 3C2 thì \(f=\frac{1}{2\pi \sqrt{L(2{{C}_{1}}+3{{C}_{2}})}}={{8.10}^{6}}Hz\) (3) Từ (1) và (2) ta được C1 = (16/9)C2 Thay vào (3) ta được : \(f=\frac{1}{2\pi \sqrt{L(2.\frac{16}{9}{{C}_{2}}+3{{C}_{2}})}}=\frac{1}{2\pi \sqrt{\frac{59}{9}L{{C}_{2}}}}=\sqrt{\frac{9}{59}{{f}_{2}}}={{3,12.10}^{6}}Hz\) Chọn A Câu hỏi 28 : Khi đặt hiệu điện thế không đổi 36 V vào hai đầu một cuộn cảm thì dòng điện qua cuộn cảm có cường độ 1,5 A. Khi đặt một điện áp xoay chiều có giá trị hiệu dụng là 200V và tần số 50Hz vào cuộn cảm thì cường độ dòng điện qua cuộn cảm có giá trị hiệu dụng là 5A. Độ tự cảm của cuộn cảm bằng
Đáp án: A Phương pháp giải: Khi đặt điện áp 1 chiều vào thì dòng điện đi qua cuộn dây cho biết điện trở của cuộn dây. Khi đặt điện áp xoay chiều thì lúc này có cuộn cảm nối tiếp với cuộn dây. Ta có định luật Ôm : \(I = \frac{U}{R};I' = \frac{{U'}}{Z} = \frac{{U'}}{{\sqrt {{R^2} + Z_L^2} }}\) Công thức tính cảm kháng : \({Z_L} = 2\pi fL\) Lời giải chi tiết: Công thức tính cảm kháng : Khi đặt điện áp 1 chiều vào thì dòng điện đi qua cuộn dây cho biết điện trở của cuộn dây. Khi đặt điện áp xoay chiều thì lúc này có cuộn cảm nối tiếp với cuộn dây. Ta có định luật Ôm : \(\left\{ \begin{array}{l} Chọn A Câu hỏi 29 : Đặt vào hai đầu tụ điện có điện dung C một điện áp xoay chiều \(u={{U}_{0}}\cos 100\pi t\)(V). Tại thời điểm t1 điện áp tức thời hai đầu đoạn mạch và dòng điện tức thời trong mạch lần lượt là \({{u}_{1}}=50\sqrt{2}\)(V); \({{i}_{1}}=\sqrt{2}\)(A). Tại thời điểm t2 điện áp tức thời hai đầu đoạn mạch và dòng điện tức thời trong mạch lần lượt là \({{u}_{2}}=50\)(V); \({{i}_{1}}=-\sqrt{3}\)(A). Giá trị của C là
Đáp án: D Phương pháp giải: Đoạn mạch chỉ chứa tụ có cường dòng điện vuông pha với điện áp hai đầu mạch nên: \({{\left( \frac{i}{{{I}_{0}}} \right)}^{2}}+{{\left( \frac{u}{{{U}_{0}}} \right)}^{2}}=1\) Biểu thức định luật Ôm cho đoạn mạch chỉ chứa tụ điện là I = U/ZC Dung kháng ZC = (ωC)-1 Lời giải chi tiết: Đoạn mạch chỉ chứa tụ có cường dòng điện vuông pha với điện áp hai đầu mạch nên: \({{\left( \frac{i}{{{I}_{0}}} \right)}^{2}}+{{\left( \frac{u}{{{U}_{0}}} \right)}^{2}}=1\) Thay số ta được: \({{\left( \frac{\sqrt{2}}{{{I}_{0}}} \right)}^{2}}+{{\left( \frac{50\sqrt{2}}{{{U}_{0}}} \right)}^{2}}=1\) \({{\left( \frac{-\sqrt{3}}{{{I}_{0}}} \right)}^{2}}+{{\left( \frac{50}{{{U}_{0}}} \right)}^{2}}=1\) Giải hệ phương trình trên ta được I0 = 2A; U0 = 100V Dung kháng của tụ: \({{Z}_{C}}=\frac{1}{\omega C}=\frac{{{U}_{0}}}{{{I}_{0}}}=50\Omega \Rightarrow C=\frac{{{10}^{-3}}}{5\pi }(F)\) Chọn D Câu hỏi 30 : Cho một đoạn mạch điện xoay chiều chỉ có cuộn dây thuần cảm. Tại thời điểm t1 điện áp và dòng điện qua cuộn cảm có giá trị lần lượt là 25 V; 0,3 A. Tại thời điểm t2 điện áp và dòng điện qua cuộn cảm có giá trị lần lượt là 15 V; 0,5 A. Cảm kháng của mạch có giá trị là
Đáp án: D Phương pháp giải: Đoạn mạch chỉ có cuộn cảm thuần thì điện áp luôn vuông pha với dòng điện. Áp dụng công thức độc lập cho hai đại lượng vuông pha${{(\frac{u}{{{U}_{o}}})}^{2}}+{{(\frac{i}{{{I}_{o}}})}^{2}}=1$ Lời giải chi tiết: Cảm kháng của mạch: \({{Z}_{L}}=\frac{{{U}_{0}}}{{{I}_{0}}}\) $\Rightarrow {{U}_{0}}={{I}_{o}}.{{Z}_{L}}$ Tại thời điểm thứ nhất: ${{(\frac{{{u}_{1}}}{{{U}_{o}}})}^{2}}+{{(\frac{{{i}_{1}}}{{{I}_{o}}})}^{2}}=1$ \(\begin{array}{l} \(\Rightarrow {{(\frac{25}{{{Z}_{L}}})}^{2}}+{{(0,3)}^{2}}=I_{0}^{2}\) (1) Tại thời điểm thứ hai: ${{(\frac{{{u}_{2}}}{{{U}_{o}}})}^{2}}+{{(\frac{{{i}_{2}}}{{{I}_{o}}})}^{2}}=1$ $\Rightarrow {{(\frac{15}{{{I}_{o}}.{{Z}_{L}}})}^{2}}+{{(\frac{0,5}{{{I}_{o}}})}^{2}}=1$ $\Rightarrow {{(\frac{15}{{{Z}_{L}}})}^{2}}+{{(0,5)}^{2}}=I_{0}^{2}$ (2) Từ (1) và (2): \(\begin{array}{l} Chọn D Câu hỏi 31 : Đặt vào hai đầu tụ điện có điện dung C một điện áp xoay chiều \(u = {U_0}\cos 100\pi t\)(V). Tại thời điểm t1 điện áp tức thời hai đầu đoạn mạch và dòng điện tức thời trong mạch lần lượt là \({u_1} = 50\sqrt 2 \)(V); \({i_1} = \sqrt 2 \)(A). Tại thời điểm t2 điện áp tức thời hai đầu đoạn mạch và dòng điện tức thời trong mạch lần lượt là \({u_2} = 50\)(V); \({i_1} = - \sqrt 3 \)(A). Giá trị của C là
Đáp án: D Phương pháp giải: Phương pháp: Đoạn mạch chỉ chứa tụ có cường dòng điện vuông pha với điện áp hai đầu mạch nên:\({\left( {\frac{i}{{{I_0}}}} \right)^2} + {\left( {\frac{u}{{{U_0}}}} \right)^2} = 1\) Biểu thức định luật Ôm cho đoạn mạch chỉ chứa tụ điện là I = U/ZC Dung kháng ZC = (ωC)-1 Lời giải chi tiết: Cách giải: Đoạn mạch chỉ chứa tụ có cường dòng điện vuông pha với điện áp hai đầu mạch nên:\({\left( {\frac{i}{{{I_0}}}} \right)^2} + {\left( {\frac{u}{{{U_0}}}} \right)^2} = 1\) Thay số ta được:\(\left\{ \begin{array}{l}{\left( {\frac{{\sqrt 2 }}{{{I_0}}}} \right)^2} + {\left( {\frac{{50\sqrt 2 }}{{{U_0}}}} \right)^2} = 1\\{\left( {\frac{{ - \sqrt 3 }}{{{I_0}}}} \right)^2} + {\left( {\frac{{50}}{{{U_0}}}} \right)^2} = 1\end{array} \right.\) Giải hệ phương trình trên ta được \({I_0}\; = 2A;{U_0}\; = 100V\) Dung kháng của tụ: \({Z_C} = \frac{1}{{\omega C}} = \frac{{{U_0}}}{{{I_0}}} = 50\Omega \Rightarrow C = \frac{{{{10}^{ - 3}}}}{{5\pi }}(F)\) Chọn D Câu hỏi 32 : Đặt vào hai đầu tụ điện có điện dung C một điện áp xoay chiều \(u = {U_0}\cos 100\pi t\)(V). Tại thời điểm t1 điện áp tức thời hai đầu đoạn mạch và dòng điện tức thời trong mạch lần lượt là \({u_1} = 50\sqrt 2 \)(V); \({i_1} = \sqrt 2 \)(A). Tại thời điểm t2 điện áp tức thời hai đầu đoạn mạch và dòng điện tức thời trong mạch lần lượt là \({u_2} = 50\)(V); \({i_1} = - \sqrt 3 \)(A). Giá trị của C là
Đáp án: D Phương pháp giải: Phương pháp: Đoạn mạch chỉ chứa tụ có cường dòng điện vuông pha với điện áp hai đầu mạch nên:\({\left( {\frac{i}{{{I_0}}}} \right)^2} + {\left( {\frac{u}{{{U_0}}}} \right)^2} = 1\) Biểu thức định luật Ôm cho đoạn mạch chỉ chứa tụ điện là I = U/ZC Dung kháng ZC = (ωC)-1 Lời giải chi tiết: Cách giải: Đoạn mạch chỉ chứa tụ có cường dòng điện vuông pha với điện áp hai đầu mạch nên:\({\left( {\frac{i}{{{I_0}}}} \right)^2} + {\left( {\frac{u}{{{U_0}}}} \right)^2} = 1\) Thay số ta được: \({\left( {\frac{{\sqrt 2 }}{{{I_0}}}} \right)^2} + {\left( {\frac{{50\sqrt 2 }}{{{U_0}}}} \right)^2} = 1\) \({\left( {\frac{{ - \sqrt 3 }}{{{I_0}}}} \right)^2} + {\left( {\frac{{50}}{{{U_0}}}} \right)^2} = 1\) Giải hệ phương trình trên ta được I0 = 2A; U0 = 100V Dung kháng của tụ: \({Z_C} = \frac{1}{{\omega C}} = \frac{{{U_0}}}{{{I_0}}} = 50\Omega \Rightarrow C = \frac{{{{10}^{ - 3}}}}{{5\pi }}(F)\) Chọn D Câu hỏi 33 : Mạch điện gồm cuộn dây thuần cảm, độ tự cảm \(L = \dfrac{1}{{4\pi }}H\)được gắn vào mạng điện xoay chiều người ta thấy dòng điện trong mạch có biểu thức là \(i = 2\cos \left( {100\pi t - \dfrac{\pi }{6}} \right)A\). Hỏi nếu gắn vào mạng điện đó đoạn mạch chỉ có tụ điện có điện dung là \(C = \dfrac{{{{10}^{ - 3}}}}{{2\pi }}\) thì dòng điện trong mạch có biểu thức là?
Đáp án: C Phương pháp giải: Cảm kháng: \({Z_L} = \omega L\) Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\) Đoạn mạch chỉ chứa cuộn cảm thuần: \(\left\{ \begin{array}{l}i = {I_0}.\cos \left( {\omega t + \varphi } \right)\\{u_L} = {I_0}.{Z_L}.\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\end{array} \right.\) Đoạn mạch chỉ chứa tụ điện: \(\left\{ \begin{array}{l}i = {I_0}.\cos \left( {\omega t + \varphi } \right)\\{u_C} = {I_0}.{Z_C}.\cos \left( {\omega t + \varphi - \dfrac{\pi }{2}} \right)\end{array} \right.\) Lời giải chi tiết: Giá trị của cảm kháng vào dung kháng là: \(\left\{ \begin{array}{l}{Z_L} = \omega L = 100\pi .\dfrac{1}{{4\pi }} = 25\Omega \\{Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 3}}}}{{2\pi }}}} = 20\Omega \end{array} \right.\) Biểu thức của i khi mạch chỉ chứa cuộn dây: \(i = 2\cos \left( {100\pi t - \dfrac{\pi }{6}} \right)A\) Biểu thức của u là: \(u = 2.{Z_L}\cos \left( {100\pi t - \dfrac{\pi }{6} + \dfrac{\pi }{2}} \right) = 50.\cos \left( {100\pi t + \dfrac{\pi }{3}} \right)V\) Khi đặt hiệu điện thế này vào hai đầu đoạn mạch chỉ chứa tụ điện thì biểu thức của i là: \(\begin{array}{l}{i_C} = \dfrac{{{U_0}}}{{{Z_C}}}\cos \left( {100\pi t + \dfrac{\pi }{3} + \dfrac{\pi }{2}} \right) = \dfrac{{50}}{{20}}\cos \left( {100\pi t + \dfrac{{5\pi }}{6}} \right)\\ \Rightarrow {i_C} = 2,5\cos \left( {100\pi t + \dfrac{{5\pi }}{6}} \right)A\end{array}\) Chọn C. Câu hỏi 34 : Mạch điện có cuộn dây thuần cảm độ tự cảm là \(L = \dfrac{{0,4}}{\pi }H\) được gắn vào mạng điện xoay chiều có phương trình \(u = 100\cos \left( {100\pi t - \dfrac{\pi }{2}} \right)V\). Viết phương trình dòng điện qua mạch khi đó? Và nếu cũng mạng điện đó ta thay cuộn dây bằng điện trở R = 20Ω thì công suất tỏa nhiệt trong mạch là bao nhiêu?
Đáp án: B Phương pháp giải: Đoạn mạch chỉ chứa cuộn cảm thuần: \(\left\{ \begin{array}{l}i = {I_0}.\cos \left( {\omega t + \varphi } \right)\\{u_L} = {I_0}.{Z_L}.\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\end{array} \right.\) Công suất toả nhiệt trên điện trở: \(P = \dfrac{{{U^2}}}{R}\) Lời giải chi tiết: Cảm kháng: ZL = ωL = 40Ω Cường độ dòng điện cực đại: \({I_0} = \dfrac{{{U_0}}}{{{Z_L}}} = \dfrac{{100}}{{40}} = 2,5A\) Khi có cuộn dây thì i chậm pha hơn u góc \(\dfrac{\pi }{2}\) Vậy pha ban đầu của i là: \({\varphi _i} = {\varphi _u} - \dfrac{\pi }{2} = - \pi {\mkern 1mu} \left( {rad} \right)\) Phương trình của i là: \(i = 2,5\cos \left( {100\pi t - \pi } \right)A\) Điện áp hiệu dụng đặt vào hai đầu đoạn mạch: \(U = \dfrac{{{U_0}}}{{\sqrt 2 }} = \dfrac{{100}}{{\sqrt 2 }} = 50\sqrt 2 V\) Nếu thay cuộn dây bằng điện trở R thì công suất tiêu thụ của đoạn mạch là: \(P = \dfrac{{{U^2}}}{R} = \dfrac{{{{\left( {50\sqrt 2 } \right)}^2}}}{{20}} = 250W\) Chọn B. Câu hỏi 35 : Mắc cuộn dây thuần cảm có độ tự cảm \(L = \dfrac{1}{\pi }H\)thì trong mạch có dòng điện \(i = 5\sqrt 2 \cos \left( {100\pi t + \dfrac{\pi }{3}} \right){\rm{ }}A\). Còn nếu thay vào đó là một điện trở 50Ω thì dòng điện trong mạch có biểu thức là
Đáp án: D Phương pháp giải: Đoạn mạch chỉ chứa cuộn cảm thuần: \(\left\{ \begin{array}{l}i = {I_0}.\cos \left( {\omega t + \varphi } \right)\\{u_L} = {I_0}.{Z_L}.\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\end{array} \right.\) Đoạn mạch chỉ có điện trở: \(\left\{ \begin{array}{l}i = {I_0}.\cos \left( {\omega t + \varphi } \right)\\u = i.R = {I_0}.R.\cos \left( {\omega t + \varphi } \right)\end{array} \right.\) Lời giải chi tiết: Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{\pi } = 100\Omega \) Biểu thức của điện áp hai đầu đoạn mạch: \(u = {I_0}.{Z_L}\cos \left( {100\pi t + \dfrac{\pi }{3} + \dfrac{\pi }{2}} \right) = 500\sqrt 2 \cos \left( {100\pi t + \dfrac{{5\pi }}{6}} \right)V\) Đặt hiệu điện thế đó vào hai đầu đoạn mạch là 1 điện trở thì biểu thức của cường độ dòng điện trong mạch là: \({i_R} = \dfrac{{{U_0}}}{R}.\cos \left( {100\pi t + \dfrac{{5\pi }}{6}} \right) = 10\sqrt 2 \cos \left( {100\pi t + \dfrac{{5\pi }}{6}} \right)A\) Chọn D. Câu hỏi 36 : Đặt điện áp xoay chiều có giá trị cực đại là \(220\sqrt 2 V\) vào hai đầu một tụ điện thì cường độ dòng điện trong cuộn cảm có biểu thức \(i = 5.\cos 100\pi t\,\,\left( A \right)\). Tại thời điểm điện áp có 220V và đang tăng thì cường độ dòng điện là:
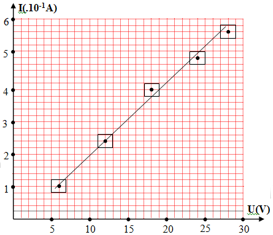
Đáp án: C Phương pháp giải: Sử dụng VTLG Mạch điện chỉ chứa tụ điện có u trễ pha hơn i góc \(\dfrac{\pi }{2}\) Lời giải chi tiết: Đối với đoạn mạch chỉ chứa tụ điện thì điện áp hai đầu mạch luôn trễ pha hơn so với dòng điện một góc \(\dfrac{\pi }{2}\) Biểu diễn trên VTLG ta có: Từ VTLG ta thấy tại thời điểm u = 220V và đang tăng thì cường độ dòng điện: \(i = {I_0}.\cos \dfrac{\pi }{4} = 5.\dfrac{{\sqrt 2 }}{2} = 2,5\sqrt 2 A\) Chọn C. Câu hỏi 37 : Một nhóm học sinh dùng vôn kế và ampe kế để khảo sát sự phụ thuộc của cường độ dòng điện vào điện áp đặt vào hai bản của một tụ điện. Đường đặc tính V – A của tụ điện vẽ theo số liệu đo được như hình bên. Biết nhóm học sinh này sử dụng dòng điện có tần số 50Hz. Điện dung của tụ điện trong thí nghiệm này là
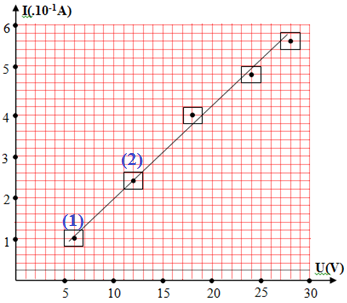
Đáp án: C Phương pháp giải: + Đọc đồ thị + Xác định điểm trên đồ thị + Sử dụng biểu thức tính dung kháng:\({Z_C} = \dfrac{1}{{\omega C}}\) Lời giải chi tiết:
Ta có, tần số góc: \(\omega = 2\pi f = 100\pi \left( {rad/s} \right)\) Từ đồ thị, ta có hệ số góc của đường thẳng chính là giá trị của \(\dfrac{1}{{{Z_C}}}\) Xét 2 điểm (1) và (2) trên đồ thị, ta có: \(\left( 1 \right)\left\{ \begin{array}{l}{I_1} = 1,{2.10^{ - 1}}A\\U = 6V\end{array} \right.\) và \(\left( 2 \right)\left\{ \begin{array}{l}{I_2} = 2,{4.10^{ - 1}}A\\{U_2} = 12V\end{array} \right.\) Ta có \(\dfrac{1}{{{Z_C}}} = \dfrac{{{I_2} - {I_1}}}{{{U_2} - {U_1}}} \Leftrightarrow \dfrac{1}{{{Z_C}}} = \dfrac{{0,24 - 0,12}}{{12 - 6}}\) \( \Rightarrow {Z_C} = 50\Omega \) Mặt khác: \({Z_C} = \dfrac{1}{{\omega C}} \Rightarrow C = \dfrac{1}{{\omega .{Z_C}}} = \dfrac{1}{{100\pi .50}} = \dfrac{{{{2.10}^{ - 4}}}}{\pi } \approx 6,{37.10^{ - 5}}F\) Chọn C Câu hỏi 38 : Một tụ điện khi mắc vào nguồn \(u = U\sqrt 2 \cos (100\pi t + \pi )\,(V)\) (U không đổi, t tính bằng s) thì cường độ hiệu dụng qua mạch là \(2\,\,A\). Nếu mắc tụ vào nguồn \(u = U\cos (120\pi t + \dfrac{\pi }{2})\,(V)\) thì cường độ hiệu dụng qua mạch là
Đáp án: D Phương pháp giải: Dung kháng của tụ điện: \({Z_C} = \dfrac{1}{{\omega C}}\) Cường độ dòng điện hiệu dụng: \(I = \dfrac{U}{{{Z_C}}}\) Lời giải chi tiết: Khi mắc nguồn \(u = U\sqrt 2 \cos (100\pi t + \pi )\,(V)\) và \(u = U\cos (120\pi t + \dfrac{\pi }{2})\,(V)\), cường độ dòng điện hiệu dụng qua tụ điện là: \(\begin{array}{l}\left\{ \begin{array}{l}{I_1} = \dfrac{{{U_1}}}{{{Z_{{C_1}}}}} = {U_1}.{\omega _1}C = U.{\omega _1}C = 2\,\,\left( A \right)\\{I_2} = \dfrac{{{U_2}}}{{{Z_{{C_2}}}}} = {U_2}.{\omega _2}C = \dfrac{U}{{\sqrt 2 }}.{\omega _2}C\end{array} \right.\\ \Rightarrow \dfrac{{{I_2}}}{{{I_1}}} = \dfrac{{{U_2}{\omega _2}}}{{{U_1}{\omega _1}}} = \dfrac{{{\omega _2}}}{{\sqrt 2 {\omega _1}}} \Rightarrow \dfrac{{{I_2}}}{2} = \dfrac{{120\pi }}{{\sqrt 2 .100\pi }} \Rightarrow {I_2} = 1,2\sqrt 2 \,\,\left( A \right)\end{array}\) Chọn D. Câu hỏi 39 : Đặt một điện áp xoay chiều \(u = {U_0}\cos \left( {\omega t} \right)\) (\({U_0}\) và ω không đổi) vào hai đầu một đoạn mạch chỉ có tụ điện có điện dung \(C\). Cường độ dòng điện qua mạch tại thời điểm \(t = \dfrac{\pi }{{2\omega }}\) có thể là
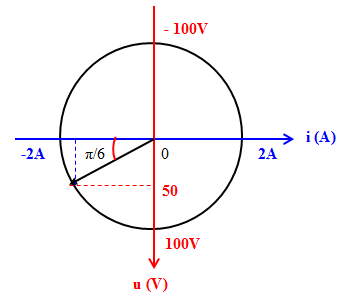
Đáp án: B Phương pháp giải: Mạch chỉ có tụ điện: \(\left\{ \begin{array}{l}u = {U_0}\cos \left( {\omega t} \right)\\i = {I_0}.\cos \left( {\omega t + \dfrac{\pi }{2}} \right)\end{array} \right.\) Thay t vào phương trình của i. Lời giải chi tiết: Mạch chỉ có tụ điện ta có: \(\left\{ \begin{array}{l}u = {U_0}\cos \left( {\omega t} \right)\\i = {I_0}.\cos \left( {\omega t + \dfrac{\pi }{2}} \right) = \dfrac{{{U_0}}}{{{Z_C}}}.\cos \left( {\omega t + \dfrac{\pi }{2}} \right) = C\omega {U_0}\cos \left( {\omega t + \dfrac{\pi }{2}} \right)\end{array} \right.\) Tại thời điểm \(t = \dfrac{\pi }{{2\omega }} \Rightarrow i = C\omega {U_0}\cos \left( {\omega .\dfrac{\pi }{{2\omega }} + \dfrac{\pi }{2}} \right) = - C\omega {U_0}\) \( \Rightarrow \left| i \right| = C\omega {U_0}\) Chọn B. Câu hỏi 40 : Đặt điện áp xoay chiều có giá trị cực đại là \(100V\) vào hai đầu một cuộn dây thuần cảm thì cường độ dòng điện trong cuộn cảm có biểu thức \(i = 2.\cos 100\pi t\,\,\left( A \right)\). Tại thời điểm điện áp có 50V và đang giảm thì cường độ dòng điện là:
Đáp án: D Phương pháp giải: Sử dụng VTLG Mạch điện chỉ chứa cuộn cảm thuần có u sớm pha hơn i góc \(\dfrac{\pi }{2}\) Lời giải chi tiết: Đối với đoạn mạch chỉ chứa cuộn cảm thuần thì điện áp hai đầu mạch luôn sớm pha hơn so với dòng điện một góc \(\dfrac{\pi }{2}\) Biểu diễn trên VTLG ta có: Từ VTLG ta thấy tại thời điểm u = 50V và đang giảm thì cường độ dòng điện: \(i = {I_0}.\cos \dfrac{\pi }{6} = 2.\dfrac{{\sqrt 3 }}{2} = \sqrt 3 A\) Chọn D. Câu hỏi 41 : Đặt vào hai đầu cuộn cảm có điện trở thuần một điện áp xoay chiều \(u = 120\cos 100\pi t\left( V \right)\). Biểu thức của cường độ dòng điện trong đoạn mạch là \(i = 3\cos \left( {100\pi t - \frac{\pi }{6}} \right){\rm{ }}A\). Độ tự cảm L của cuộn dây gân nhất với giá trị nào sau đây?
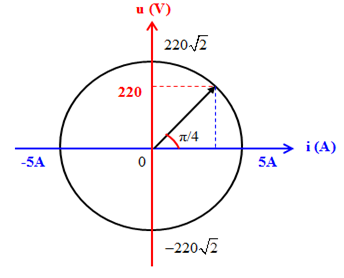
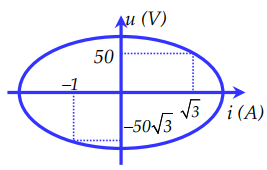
Đáp án: D Phương pháp giải: Biểu thức định luật Ôm: \({I_0} = \frac{{{U_0}}}{Z} \Rightarrow Z = \frac{{{U_0}}}{{{I_0}}}\) Độ lệch pha giữa u và i: \(\tan \varphi = \frac{{{Z_L}}}{R}\) Biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + Z_L^2} \) Công thức tính cảm kháng: \({Z_L} = \omega L\) Lời giải chi tiết: + Ta có: \({I_0} = \frac{{{U_0}}}{Z} \Rightarrow Z = \frac{{{U_0}}}{{{I_0}}} = \frac{{120}}{3} = 40\Omega \) + Độ lệch pha giữa u và i: \(\tan \varphi = \frac{{{Z_L}}}{R} \Rightarrow \frac{{{Z_L}}}{R} = \tan \frac{\pi }{6} = \frac{1}{{\sqrt 3 }} \Leftrightarrow R = \sqrt 3 {Z_L}\) Tổng trở của đoạn mạch: \(Z = \sqrt {{R^2} + Z_L^2} = 2{Z_L} \Rightarrow {Z_L} = 20\Omega \) Cảm kháng: \({Z_L} = \omega L \Rightarrow L = \frac{{{Z_L}}}{\omega } = \frac{2}{{10\pi }} = 63,7mH\) Vậy giá trị của L gần nhất với 65mH. Chọn D. Câu hỏi 42 : Cho đồ thị biểu diễn mối liên hệ giữa u và i trong mạch điện xoay chiều chỉ có L như hình vẽ. Xác định giá trị cảm kháng của cuộn cảm:
Đáp án: C Phương pháp giải: Đối với đoạn mạch chỉ chứa cuộn cảm: \(\left\{ \begin{array}{l} Vì u và i vuông pha với nhau nên ta có \(\frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\), đồ thị u phụ thuộc vào i là một elip. Từ đồ thị ta xác định được hai vị trí tọa độ: \(\left\{ \begin{array}{l} thay vào phương trình trên tìm được U0 và I0. Và theo định luật Ôm ta có \({U_0} = {I_0}.{Z_L}\) Lời giải chi tiết: Đối với đoạn mạch chỉ chứa cuộn cảm: \(\left\{ \begin{array}{l} Vì u và i vuông pha với nhau nên: \(\frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\) → Đồ thị u phụ thuộc vào i là một elip. Từ đồ thị ta xác định được hai vị trí có tọa độ: \(\left\{ \begin{array}{l} Thay vào (*) được: \(\left\{ \begin{array}{l} Áp dụng định luật Ôm: \({I_0} = \frac{{{U_0}}}{{{Z_L}}} \Rightarrow {Z_L} = \frac{{{U_0}}}{{{I_0}}} = \frac{{100}}{2} = 50\Omega \) Chọn C. Câu hỏi 43 : Đặt điện áp xoay chiều \(u = {U_0}\cos \left( {100\pi t + \dfrac{\pi }{3}} \right)V\)vào hai đầu một cuộn cảm thuần có độ tự cảm \(L = \dfrac{1}{{2\pi }}H\). Ở thời điểm điện áp giữa hai đầu cuộn cảm là \(100\sqrt 2 {\rm{ }}V\)thì cường độ dòng điện qua cuộn cảm là 2A. Biểu thức của cường độ dòng điện qua cuộn cảm là
Đáp án: A Phương pháp giải: Mạch chỉ có cuộn cảm nên \(u \bot i \Rightarrow \dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1\) Đối với cuộn cảm thuần: \(\left\{ \begin{array}{l}i = {I_0}.\cos \left( {\omega t + \varphi } \right)\\{u_L} = {I_0}.{Z_L}.\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\end{array} \right.\) Lời giải chi tiết: Cảm kháng của cuộn cảm: \({Z_L} = \omega L = 100\pi .\dfrac{1}{{2\pi }} = 50\Omega \) Điện áp cực đại: \({U_0} = {I_0}{Z_C} = 50{I_0}\) \(\dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1 \Leftrightarrow \dfrac{{{{\left( {100\sqrt 2 } \right)}^2}}}{{{{50}^2}.I_0^2}} + \dfrac{{{2^2}}}{{I_0^2}} = 1 \Rightarrow {I_0} = 2\sqrt 3 A\) Mạch chỉ có cuộn cảm thuần nên i trễ pha hơn u góc \(\dfrac{\pi }{2}\) \( \Rightarrow {\varphi _i} = \dfrac{\pi }{3} - \dfrac{\pi }{2} = - \dfrac{\pi }{6}\) Phương trình của i là: \(i = 2\sqrt 3 \cos \left( {100\pi t - \dfrac{\pi }{6}} \right)A\) Chọn A. Câu hỏi 44 : Đặt một điện áp xoay chiều \(u = U\sqrt 2 cos\left( {100\pi t - \dfrac{\pi }{6}} \right)V\) vào hai đầu đoạn mạch chỉ có tụ điện với điện dung \(C = \dfrac{{{{10}^{ - 4}}}}{\pi }F\). Ở thời điểm t, khi điện áp hai đầu tụ điện có giá trị \(150V\) thì cường độ dòng điện trong mạch là \(2A\). Giá trị điện áp U là
Đáp án: C Phương pháp giải: + Sử dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\) + Sử dụng biểu thức: \({I_0} = \dfrac{{{U_0}}}{{{Z_C}}}\) + Sử dụng biểu thức độc lập: \({\left( {\dfrac{u}{{{U_0}}}} \right)^2} + {\left( {\dfrac{i}{{{I_0}}}} \right)^2} = 1\) Lời giải chi tiết: Ta có: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \) Mạch chỉ có tụ, ta có: \({\left( {\dfrac{u}{{{U_0}}}} \right)^2} + {\left( {\dfrac{i}{{{I_0}}}} \right)^2} = 1\) \(\begin{array}{l} \Leftrightarrow {\left( {\dfrac{u}{{{U_0}}}} \right)^2} + {\left( {\dfrac{i}{{\dfrac{{{U_0}}}{{{Z_C}}}}}} \right)^2} = 1\\ \Leftrightarrow \dfrac{{{{150}^2}}}{{U_0^2}} + \dfrac{{{2^2}}}{{\dfrac{{U_0^2}}{{{{100}^2}}}}} = 1\\ \Rightarrow {U_0} = 250V\\ \Rightarrow U = \dfrac{{{U_0}}}{{\sqrt 2 }} = 125\sqrt 2 V\end{array}\) Chọn C Câu hỏi 45 : Đặt vào hai đầu cuộn thuần cảm với độ tự cảm \(L = \frac{1}{\pi }H\) một hiệu điện thế xoay chiều \(u = {U_0}.\cos 100\pi t\left( V \right).\)Tại thời điểm t1có \({u_1} = 200V,{i_1}\; = 2A\); tại thời điểm t2có \({u_2} = 200\sqrt 2 V,{i_2} = 0\). Biểu thức của hiệu điện thế và dòng điện trong mạch là
Đáp án: A Phương pháp giải: Đoạn mạch xoay chiều chỉ chứa cuộn cảm thuần thì: + Điện áp và cường độ dòng điện vuông pha với nhau. Ta có: \(\frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\) + Cường độ dòng điện trễ pha \(\frac{\pi }{2}\) so với điện áp. Lời giải chi tiết: Đoạn mạch xoay chiều chỉ chứa cuộn cảm thuần thì điện áp và cường độ dòng điện vuông pha với nhau. Ta có: \(\begin{array}{l} Chọn A. Câu hỏi 46 : Đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số f thay đổi được vào hai đầu một cuộn tụ điện. Khi f = 50Hz thì cường độ dòng điện qua tụ điện có giá trị hiệu dụng bằng 3A. Khi f = 60Hz thì cường độ dòng điện qua tụ điện có giá trị hiệu dụng bằng
Đáp án: A Phương pháp giải: Cường độ dòng điện hiệu dụng qua tụ : \(I = \dfrac{U}{{{Z_C}}} = \dfrac{U}{{\dfrac{1}{{\omega C}}}} = U.C.2\pi f\) Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}{I_1} = \dfrac{U}{{{Z_{C1}}}} = U.C.2\pi {f_1}\\{I_2} = \dfrac{U}{{{Z_{C2}}}} = U.C.2\pi {f_2}\end{array} \right. \Rightarrow \dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{{f_1}}}{{{f_2}}} = \dfrac{5}{6} \Rightarrow {I_2} = \dfrac{6}{5}.3 = 3,6A\) Chọn A. Câu hỏi 47 : Đặt điện áp xoay chiều \(u = {U_0}\cos \left( {100\pi t-\dfrac{\pi }{3}} \right)V\)vào hai đầu một cuộn cảm thuần có độ tự cảm \(L = \dfrac{1}{{2\pi }}H\). Ở thời điểm điện áp giữa hai đầu cuộn cảm là \(100\sqrt 2 {\rm{ }}V\)thì cường độ dòng điện qua cuộn cảm là 2A. Biểu thức của cường độ dòng điện qua cuộn cảm là
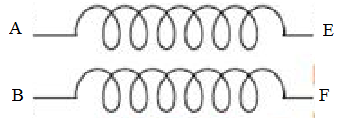
Đáp án: A Phương pháp giải: Mạch chỉ có cuộn cảm nên \(u \bot i \Rightarrow \dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1\) Đối với cuộn cảm thuần: \(\left\{ \begin{array}{l}i = {I_0}.\cos \left( {\omega t + \varphi } \right)\\{u_L} = {I_0}.{Z_L}.\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\end{array} \right.\) Lời giải chi tiết: Cảm kháng của cuộn cảm: \({Z_L} = \omega L = 100\pi .\dfrac{1}{{2\pi }} = 50\Omega \) Điện áp cực đại: \({U_0} = {I_0}{Z_C} = 50{I_0}\) \(\dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1 \Leftrightarrow \dfrac{{{{\left( {100\sqrt 2 } \right)}^2}}}{{{{50}^2}.I_0^2}} + \dfrac{{{2^2}}}{{I_0^2}} = 1 \Rightarrow {I_0} = 2\sqrt 3 A\) Mạch chỉ có cuộn cảm thuần nên i trễ pha hơn u góc \(\dfrac{\pi }{2}\) \( \Rightarrow {\varphi _i} = - \dfrac{\pi }{3} - \dfrac{\pi }{2} = - \dfrac{{5\pi }}{6}\) Phương trình của i là: \(i = 2\sqrt 3 \cos \left( {100\pi t - \dfrac{{5\pi }}{6}} \right)A\) Chọn A. Câu hỏi 48 : Một học sinh mắc mạch điện như hình vẽ. Đặt vào A và B điện áp xoay chiều (U không đổi). Khi nối E, F với một ampe kế thì số chỉ của ampe kế là 3,8A. Khi nối E, F với một vôn kế thì số chỉ của vôn kế là 11,95V. Coi như hai cuộn dây thuần cảm và có hệ số tự cảm bằng nhau. Độ tự cảm cảu mỗi cuộn dây gần nhấu với giá trị nào sau đây?
Đáp án: A Phương pháp giải: Khi mắc ampe kế vào E,F ta đo được cường độ dòng điện chạy trong mạch : \(I = \frac{U}{{2{Z_L}}}\) Khi mắc Vôn kế vào E, F thì ta đo được hiệu điện thế giữa hai điểm E, F tức là A, B (vì vôn kế lý tưởng và mạch thuần cảm). Vậy là U = 11,95 V. Cảm kháng: \({Z_L} = \omega .L\) Lời giải chi tiết: Khi mắc ampe kế vào E,F ta đo được cường độ dòng điện chạy trong mạch : \(I = \frac{U}{{2{Z_L}}} \Rightarrow {Z_L} = \frac{U}{{2I}}\) Khi mắc Vôn kế vào E, F thì ta đo được hiệu điện thế giữa hai điểm E, F tức là A, B (vì vôn kế lý tưởng và mạch thuần cảm). Vậy là U = 11,95V. Lại có : \(I = \frac{U}{{2{Z_L}}} \Rightarrow {Z_L} = \frac{U}{{2I}} = \frac{{11,95}}{{2.3,8}} = 1,{572_{}}\Omega \) Từ công thức tính cảm kháng ta có : \(L = \frac{{{Z_L}}}{\omega } = \frac{{1,572}}{{100\pi }} = {5.10^{ - 3}}H = 5mH\) Chọn A. Câu hỏi 49 : Mạch điện xoay chiều chỉ chứa tụ điện \(C = \dfrac{1}{{7200\pi }}F\), hiệu điện thế xoay chiều ổn định đặt vào hai đầu mạch là\(u = {U_0}\cos \left( {\omega t + \dfrac{\pi }{4}} \right){\rm{ }}V\). Tại thời điểm t1 ta có \({u_1} = 60\sqrt 2 V;{i_1} = \dfrac{{\sqrt 2 }}{2}A\), tại thời điểm t2 ta có \({u_2} = - 60\sqrt 3 V;{i_2} = - 0,5A\). Hãy hoàn thiện biểu thức của điện áp u.
Đáp án: D Phương pháp giải: Mạch chỉ có tụ điện nên \(u \bot i \Rightarrow \dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1\) Lời giải chi tiết: Tại thời điểm t1 và t2 ta có: \(\begin{array}{l}\left\{ \begin{array}{l}\dfrac{{{{\left( {60\sqrt 2 } \right)}^2}}}{{U_0^2}} + \dfrac{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}}{{I_0^2}} = 1\\\dfrac{{{{\left( { - 60\sqrt 3 } \right)}^2}}}{{U_0^2}} + \dfrac{{{{\left( { - 0,5} \right)}^2}}}{{I_0^2}} = 1\end{array} \right.\\ \Leftrightarrow \dfrac{{{{\left( {60\sqrt 2 } \right)}^2} - {{\left( { - 60\sqrt 3 } \right)}^2}}}{{U_0^2}} = \dfrac{{{{\left( { - 0,5} \right)}^2} - {{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}}{{I_0^2}}\\ \Rightarrow \dfrac{{U_0^2}}{{I_0^2}} = \dfrac{{{{\left( {60\sqrt 2 } \right)}^2} - {{\left( { - 60\sqrt 3 } \right)}^2}}}{{{{\left( { - 0,5} \right)}^2} - {{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}} = 14400\\ \Rightarrow \dfrac{{{U_0}}}{{{I_0}}} = 120 \Rightarrow {Z_C} = 120\Omega \\ \Rightarrow \dfrac{1}{{\omega C}} = 120 \Rightarrow \omega = \dfrac{1}{{120.C}} = \dfrac{1}{{120.\dfrac{1}{{7200\pi }}}} = 60\pi \,\left( {rad/s} \right)\end{array}\) Vậy biểu thức của u là: \(u = {U_0}\cos \left( {60\pi t + \dfrac{\pi }{4}} \right)V\) Chọn D. Câu hỏi 50 : Đặt điện áp xoay chiều có giá trị cực đại là \(100V\) vào hai đầu một cuộn dây thuần cảm thì cường độ dòng điện trong cuộn cảm có biểu thức \(i = 2.\cos 100\pi t\,\,\left( A \right)\). Tại thời điểm điện áp có 50V và đang tăng thì cường độ dòng điện là:
Đáp án: C Phương pháp giải: Sử dụng VTLG Mạch điện chỉ chứa cuộn cảm thuần có u sớm pha hơn i góc \(\dfrac{\pi }{2}\) Lời giải chi tiết: Đối với đoạn mạch chỉ chứa cuộn cảm thuần thì điện áp hai đầu mạch luôn sớm pha hơn so với dòng điện một góc \(\dfrac{\pi }{2}\) Biểu diễn trên VTLG ta có: Từ VTLG ta thấy tại thời điểm u = 50V và đang tăng thì cường độ dòng điện: \(i = - {I_0}.\cos \dfrac{\pi }{6} = - 2.\dfrac{{\sqrt 3 }}{2} = - \sqrt 3 A\) Chọn C.
|













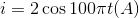 . Tại thời điểm điện áp có 50 V và đang tăng thì cường độ dòng điện là
. Tại thời điểm điện áp có 50 V và đang tăng thì cường độ dòng điện là