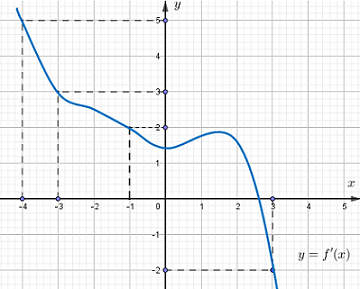
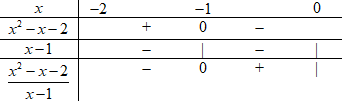40 bài tập trắc nghiệm tích phân mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Cho hàm số \(f\left( x \right)\). Biết hàm số \(y = f'\left( x \right)\) có đồ thị như hình bên. Trên đoạn \(\left[ { - 4;3} \right]\), hàm số \(g\left( x \right) = 2f\left( x \right) + {\left( {1 - x} \right)^2}\) đạt giá trị nhỏ nhất tại điểm:
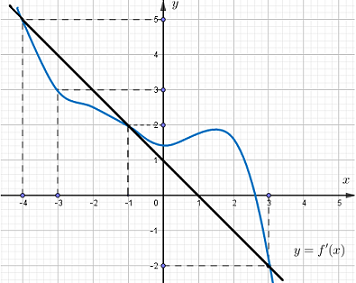
Đáp án: B Phương pháp giải: - Tính \(g'\left( x \right)\) và tìm nghiệm của \(g'\left( x \right) = 0\) trong đoạn \(\left[ { - 4;3} \right]\). - Tính giá trị của hàm số \(y = g\left( x \right)\) tại các điểm \( - 4;3\) và các điểm làm cho \(g'\left( x \right) = 0\). - So sánh các giá trị trên và kết luận GTNN. Lời giải chi tiết: Ta có: \(g'\left( x \right) = 2f'\left( x \right) - 2\left( {1 - x} \right) = 2\left[ {f'\left( x \right) - 1 + x} \right]\). \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = 1 - x\). Từ hình vẽ ta thấy, trên đoạn \(\left[ { - 4;3} \right]\) thì đường thẳng \(y = 1 - x\) cắt đồ thị hàm số \(y = f'\left( x \right)\) tại \(3\) điểm lần lượt có hoành độ \( - 4; - 1;3\) nên ta so sánh các giá trị \(g\left( { - 4} \right),g\left( { - 1} \right),g\left( 3 \right)\).
Ta thấy: \({S_1} = \int\limits_{ - 4}^{ - 1} {\left[ {1 - x - f'\left( x \right)} \right]dx} = \int\limits_{ - 4}^{ - 1} {\left[ { - g'\left( x \right)} \right]dx} = g\left( { - 4} \right) - g\left( { - 1} \right) > 0 \Rightarrow g\left( { - 4} \right) > g\left( { - 1} \right)\). \({S_2} = \int\limits_{ - 1}^3 {\left[ {f'\left( x \right) - 1 + x} \right]dx} = \int\limits_{ - 1}^3 {\left[ {g'\left( x \right)} \right]dx} = g\left( 3 \right) - g\left( { - 1} \right) > 0 \Rightarrow g\left( 3 \right) > g\left( { - 1} \right)\). Do đó \(g\left( { - 1} \right)\) là GTNN của hàm số \(y = g\left( x \right)\) hay hàm số đạt GTNN tại \({x_0} = - 1\). Chọn B Câu hỏi 2 : Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ {0;1} \right]\) thỏa mãn \(3xf\left( {{x^2}} \right) - f\left( x \right) = 9{x^3} - 1\). Tính \(\int\limits_0^1 {f\left( x \right)dx} \).
Đáp án: A Phương pháp giải: Sử dụng phương pháp tích phân 2 vế. Lời giải chi tiết: Ta có: \(3xf\left( {{x^2}} \right) - f\left( x \right) = 9{x^3} - 1\), (\(f\left( x \right)\) liên tục trên \(\left[ {0;1} \right]\)) \( \Rightarrow \int\limits_0^1 {\left( {3xf\left( {{x^2}} \right) - f\left( x \right)} \right)} dx = \int\limits_0^1 {\left( {9{x^3} - 1} \right)} dx \Leftrightarrow 3\int\limits_0^1 {xf\left( {{x^2}} \right)} dx - \int\limits_0^1 {f\left( x \right)} dx = \left. {\left( {\dfrac{9}{4}{x^4} - x} \right)} \right|_0^1\) \( \Leftrightarrow \dfrac{3}{2}\int\limits_0^1 {f\left( {{x^2}} \right)} d\left( {{x^2}} \right) - \int\limits_0^1 {f\left( x \right)} dx = \dfrac{5}{4} \Leftrightarrow \dfrac{3}{2}\int\limits_0^1 {f\left( t \right)} dt - \int\limits_0^1 {f\left( x \right)} dx = \dfrac{5}{4},\,\,\left( {t = {x^2}} \right)\) \( \Leftrightarrow \dfrac{3}{2}\int\limits_0^1 {f\left( x \right)} dx - \int\limits_0^1 {f\left( x \right)} dx = \dfrac{5}{4} \Leftrightarrow \dfrac{1}{2}\int\limits_0^1 {f\left( x \right)} dx = \dfrac{5}{4} \Leftrightarrow \int\limits_0^1 {f\left( x \right)} dx = \dfrac{5}{2}\). Chọn: A Câu hỏi 3 : Khẳng định nào sau đây đúng về kết quả \(\int\limits_1^e {{x^3}} \ln xdx = \dfrac{{3{e^a} + 1}}{b}\) ?
Đáp án: A Phương pháp giải: Tính tích phân theo phương pháp từng phần. Đặt \(\left\{ \begin{array}{l}u = \ln x\\dv = {x^3}dx\end{array} \right.\). Lời giải chi tiết: Đặt \(\left\{ \begin{array}{l}u = \ln x\\dv = {x^3}dx\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}du = \dfrac{1}{x}dx\\v = \dfrac{{{x^4}}}{4}\end{array} \right.\) Khi đó \(\int\limits_1^e {{x^3}} \ln xdx = \left. {\ln x.\dfrac{{{x^4}}}{4}} \right|_1^e - \dfrac{1}{4}\int\limits_1^e {{x^3}dx} = \dfrac{{{e^4}}}{4} - \dfrac{1}{4}.\dfrac{1}{4}\left. {{x^4}} \right|_1^e = \dfrac{{{e^4}}}{4} - \dfrac{1}{{16}}\left( {{e^4} - 1} \right) = \dfrac{{3{e^4} + 1}}{{16}}\). Do đó \(a = 4,b = 16 \Rightarrow ab = 64\). Chọn A Câu hỏi 4 : Biết \(\int\limits_0^1 {\sqrt {{x^2} + 4} .xdx} = \dfrac{1}{a}\left( {\sqrt {{b^3}} - c} \right)\). Tính \(Q = abc\).
Đáp án: A Phương pháp giải: Đặt \(t = \sqrt {{x^2} + 4} \), đổi cận và tính tích phân. Lời giải chi tiết: Đặt \(t = \sqrt {{x^2} + 4} \)\( \Rightarrow {x^2} + 4 = {t^2} \Rightarrow xdx = tdt\). Đổi cận \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 2\\x = 1 \Rightarrow t = \sqrt 5 \end{array} \right.\). Khi đó \(\int\limits_0^1 {\sqrt {{x^2} + 4} .xdx} = \int\limits_2^{\sqrt 5 } {{t^2}dt} = \left. {\dfrac{{{t^3}}}{3}} \right|_2^{\sqrt 5 } = \dfrac{1}{3}\left( {\sqrt {{5^3}} - 8} \right)\) Do đó \(a = 3,b = 5,c = 8 \Rightarrow abc = 120\). Chọn A Câu hỏi 5 : Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {1;3} \right]\), \(F\left( 1 \right) = 3,F\left( 3 \right) = 5\) và \(\int\limits_1^3 {\left( {{x^4} - 8x} \right)f\left( x \right)dx} = 12\). Tính \(I = \int\limits_1^3 {\left( {{x^3} - 2} \right)F\left( x \right)dx} \).
Đáp án: A Phương pháp giải: Sử dụng phương pháp nguyên hàm từng phần, đặt \(\left\{ \begin{array}{l}u = {x^4} - 8x\\dv = f\left( x \right)dx\end{array} \right.\) Lời giải chi tiết: Đặt \(\left\{ \begin{array}{l}u = {x^4} - 8x\\dv = f\left( x \right)dx\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}du = 4{x^3} - 8\\v = F\left( x \right)\end{array} \right.\). Khi đó \(12 = \int\limits_1^3 {\left( {{x^4} - 8x} \right)f\left( x \right)dx} \)\( = \left. {\left[ {\left( {{x^4} - 8x} \right).F\left( x \right)} \right]} \right|_1^3 - \int\limits_1^3 {\left( {4{x^3} - 8} \right)F\left( x \right)dx} \) \(\begin{array}{l} = 57.F\left( 3 \right) - \left( { - 7} \right).F\left( 1 \right) - 4\int\limits_1^3 {\left( {{x^3} - 2} \right)F\left( x \right)dx} = 57.5 + 7.3 - 4I = 306 - 4I\\ \Rightarrow 12 = 306 - 4I \Leftrightarrow I = \dfrac{{147}}{2}\end{array}\) Chọn A Câu hỏi 6 : Cho hàm số \(y = f\left( x \right)\) là hàm số chẵn, liên tục trên đoạn \(\left[ { - 2;2} \right]\) và \(\int\limits_{ - 2}^2 {\frac{{f\left( x \right)}}{{{{2018}^x} + 1}}dx = 2020} \). Khi đó, tích phân \(\int\limits_0^2 {\left( {1 + f\left( x \right)} \right)dx} \) bằng:
Đáp án: B Phương pháp giải: Sử dụng tính chất của hàm số chẵn. Lời giải chi tiết: \(\int\limits_{ - 2}^2 {\frac{{f\left( x \right)}}{{{{2018}^x} + 1}}dx = 2020} \,\,(1) \Rightarrow \int\limits_2^{ - 2} {\frac{{f\left( { - x} \right)}}{{{{2018}^{ - x}} + 1}}\left( { - dx} \right) = 2020 \Leftrightarrow } \int\limits_{ - 2}^2 {\frac{{{{2018}^x}f\left( x \right)}}{{{{2018}^x} + 1}}dx = 2020} \,\,\,(2)\) (do \(y = f\left( x \right)\) là hàm số chẵn, liên tục trên đoạn \(\left[ { - 2;2} \right]\)) Cộng (1) với (2): \(\begin{array}{l}\,\,\,\,\,\,\int\limits_{ - 2}^2 {\frac{{f\left( x \right)}}{{{{2018}^x} + 1}}dx + } \,\int\limits_{ - 2}^2 {\frac{{{{2018}^x}f\left( x \right)}}{{{{2018}^x} + 1}}dx = 4040} \\ \Leftrightarrow \int\limits_{ - 2}^2 {\left( {\frac{{f\left( x \right)}}{{{{2018}^x} + 1}} + \frac{{{{2018}^x}f\left( x \right)}}{{{{2018}^x} + 1}}} \right)dx} = 4040 \Leftrightarrow \int\limits_{ - 2}^2 {f\left( x \right)dx} = 4040\end{array}\) Lại do \(y = f\left( x \right)\) là hàm chẵn nên \(\int\limits_{ - 2}^2 {f\left( x \right)dx} = 2.\int\limits_0^2 {f\left( x \right)dx} \Rightarrow \int\limits_0^2 {f\left( x \right)dx} = 2020\) Ta có: \(\int\limits_0^2 {\left( {1 + f\left( x \right)} \right)dx} = \int\limits_0^2 {dx} + \int\limits_0^2 {f\left( x \right)dx} = 2 + 2020 = 2022\). Chọn: B Câu hỏi 7 : Biết \(\int\limits_0^1 {\frac{{{x^2} + 2x}}{{{{\left( {x + 3} \right)}^2}}}dx = \frac{a}{4} - 4\ln \frac{4}{b}} ,\) với \(a,b\) là các số nguyên dương. Giá trị của biểu thức \({a^2} + {b^2}\) bằng
Đáp án: D Phương pháp giải: Phân tích biểu thức dưới dấu tích phân về tổng, hiệu các hàm phân thức cơ bản rồi sử dụng công thức tích phân cơ bản. Lời giải chi tiết: Ta có: \(I = \int\limits_0^1 {\frac{{{x^2} + 2x}}{{{{\left( {x + 3} \right)}^2}}}dx} \) \( = \int\limits_0^1 {\frac{{{x^2} + 2x}}{{{x^2} + 6x + 9}}dx} \) \( = \int\limits_0^1 {\left[ {1 - \frac{{4x + 9}}{{{{\left( {x + 3} \right)}^2}}}} \right]dx} \) \( = \left. x \right|_0^1 - \int\limits_0^1 {\frac{{4x + 9}}{{{{\left( {x + 3} \right)}^2}}}dx} \) \( = 1 - J\) Với \(J = \int\limits_0^1 {\frac{{4x + 9}}{{{{\left( {x + 3} \right)}^2}}}dx} \) \( = \int\limits_0^1 {\frac{{4x + 12 - 3}}{{{{\left( {x + 3} \right)}^2}}}dx} \) \( = \int\limits_0^1 {\left[ {\frac{4}{{x + 3}} - \frac{3}{{{{\left( {x + 3} \right)}^2}}}} \right]dx} \) \( = 4.\int\limits_0^1 {\frac{{dx}}{{x + 3}}} - 3.\int\limits_0^1 {\frac{{dx}}{{{{\left( {x + 3} \right)}^2}}}} \) \( = 4\int\limits_0^1 {\frac{{d\left( {x + 3} \right)}}{{x + 3}}} - 3.\int\limits_0^1 {\frac{{d\left( {x + 3} \right)}}{{{{\left( {x + 3} \right)}^2}}}} \) \( = \left. {\left( {4\ln \left| {x + 3} \right| + \frac{3}{{x + 3}}} \right)} \right|_0^1\) \( = 4\ln 4 + \frac{3}{4} - 4\ln 3 - 1 = 4\ln \frac{4}{3} - \frac{1}{4}\) Do đó \(I = 1 - J = 1 - \left( {4\ln \frac{4}{3} - \frac{1}{4}} \right) = \frac{5}{4} - 4\ln \frac{4}{3}\)\( \Rightarrow a = 5,b = 3\) \( \Rightarrow {a^2} + {b^2} = {5^2} + {3^2} = 34\). Chọn D. Câu hỏi 8 : Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Biết rằng \(\int\limits_0^{\ln 2} {f\left( {{e^x} + 1} \right)dx = 5} \) và \(\int\limits_2^3 {\dfrac{{\left( {2x - 3} \right)f\left( x \right)}}{{x - 1}}dx} = 3\). Tính \(I = \int\limits_2^3 {f\left( x \right)} dx\).
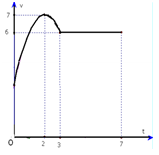
Đáp án: B Phương pháp giải: Đặt ẩn phụ \(t = {e^x} + 1\). Lời giải chi tiết: Đặt \(t = {e^x} + 1 \Rightarrow dt = {e^x}dx \Rightarrow \dfrac{{dt}}{{t - 1}} = dx\). Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 2\\x = \ln 2 \Rightarrow t = 3\end{array} \right.\) Khi đó: \(\int\limits_0^{\ln 2} {f\left( {{e^x} + 1} \right)dx = } \int\limits_2^3 {\dfrac{{f\left( t \right)dt}}{{t - 1}} = } \,5 \Rightarrow \int\limits_2^3 {\dfrac{{f\left( x \right)dx}}{{x - 1}} = } \,5\) Ta có: \(\int\limits_2^3 {\dfrac{{\left( {2x - 3} \right)f\left( x \right)}}{{x - 1}}dx} = 3 \Leftrightarrow \int\limits_2^3 {\left( {2f\left( x \right) - \dfrac{{f\left( x \right)}}{{x - 1}}} \right)dx} = 3 \Leftrightarrow 2\int\limits_2^3 {f\left( x \right)dx - \int\limits_2^3 {\dfrac{{f\left( x \right)}}{{x - 1}}dx} } = 3\)\( \Leftrightarrow 2\int\limits_2^3 {f\left( x \right)dx - 5} = 3 \Leftrightarrow \int\limits_2^3 {f\left( x \right)dx} = 4\)\( \Rightarrow I = 4\). Chọn: B Câu hỏi 9 : Một vật chuyển động trong 7 giờ với vận tốc \(v\,\,\left( {km/h} \right)\) phụ thuộc vào thời gian \(t\,\left( h \right)\) có đồ thị của vận tốc như hình dưới đây. Trong khoảng thời gian 3 giờ kể từ bắt đầu chuyển động, đồ thị là phần Parabol có đỉnh \(I\left( {2;7} \right)\), trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là đoạn thẳng song song trục hoành. Tính quãng đường \(S\) mà vật di chuyển trong 7 giờ đó.
Đáp án: B Phương pháp giải: - Lập hàm vận tốc trên đoạn từ \(\left[ {0;7} \right],\left( s \right)\) - Quãng đường: \(S = \int\limits_0^7 {v\left( t \right)dt} \). Lời giải chi tiết: Giả sử phương trình đường parabol (P) là \(y = a{x^2} + bx + c,\left( {a \ne 0} \right)\) (P) có đỉnh là \(I\left( {2;7} \right)\), đồng thời đi qua điểm (3;6) nên ta có hệ phương trình: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\4a + 2b + c = 7\\9a + 3b + c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + b = 0\\4a + 2b + c = 7\\9a + 3b + c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 4\\c = 3\end{array} \right. \Rightarrow \left( P \right):y = - {x^2} + 4x + 3\) Ta có hàm số sau: \(v\left( t \right) = \left\{ \begin{array}{l} - {t^2} + 4t + 3,\,\,\,\,\,0 \le t \le 3\\\,\,\,\,\,\,\,\,\,\,6\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,t > 3\,\end{array} \right.\) Quãng đường cần tìm là : \(\begin{array}{l}S = \int\limits_0^7 {v\left( t \right)dt} = \int\limits_0^3 {v\left( t \right)dt} + \int\limits_3^7 {v\left( t \right)dt} = \int\limits_0^3 {\left( { - {t^2} + 4t + 3} \right)dt} + \int\limits_3^7 {6dt} \\ = \left. {\left( { - \frac{1}{3}{t^3} + 2{t^2} + 3t} \right)} \right|_0^3 + 6.\left( {7 - 3} \right) = 18 + 24 = 42\,\,\left( {km} \right)\end{array}\) Chọn: B Câu hỏi 10 : Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}{\rm{\backslash }}\left\{ 0 \right\}\) và \(f\left( x \right) + 2f\left( {\frac{1}{x}} \right) = 3x,\,\forall x \ne 0\). Tính \(I = \int\limits_1^2 {f\left( x \right)dx} \)?
Đáp án: C Phương pháp giải: Xác định hàm số \(f\left( x \right)\), từ đó tính tích phân \(I = \int\limits_1^2 {f\left( x \right)dx} \). Lời giải chi tiết: Với mọi \(x \ne 0\), ta có: \(f\left( x \right) + 2f\left( {\frac{1}{x}} \right) = 3x\,\, \Rightarrow f\left( {\frac{1}{x}} \right) + 2f\left( x \right) = \frac{3}{x}\,\)\(\begin{array}{l} \Rightarrow \left( {f\left( x \right) + 2f\left( {\frac{1}{x}} \right)} \right) - 2\left( {f\left( {\frac{1}{x}} \right) + 2f\left( x \right)} \right) = 3x - \frac{6}{x} \Leftrightarrow - 3f\left( x \right) = 3x - \frac{6}{x}\\ \Leftrightarrow f\left( x \right) = \frac{2}{x} - x\end{array}\) Khi đó: \(I = \int\limits_1^2 {f\left( x \right)dx} = \int\limits_1^2 {\left( {\frac{2}{x} - x} \right)dx} = \left. {\left( {2\ln \left| x \right| - \frac{1}{2}{x^2}} \right)} \right|_1^2 = 2\ln 2 - \frac{3}{2}\). Chọn: C Câu hỏi 11 : Cho \(I = \int\limits_0^1 {\dfrac{{dx}}{{\sqrt {2x + m} }}} \) , \(m\) là số thực dương. Tìm tất cả các giá trị của \(m\) để \(I \ge 1.\)
Đáp án: A Phương pháp giải: Sử dụng công thức \(\int {{{\left( {ax + b} \right)}^n}dx} = \dfrac{1}{a}\dfrac{{{{\left( {ax + b} \right)}^{n + 1}}}}{{n + 1}} + C\,\left( {n \ne - 1} \right)\) và \(\int\limits_a^b {f\left( x \right)dx} = \left. {F\left( x \right)} \right|_a^b = F\left( b \right) - F\left( a \right)\) với \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right).\) Lời giải chi tiết: Ta có \(\int\limits_0^1 {\dfrac{{dx}}{{\sqrt {2x + m} }} = \int\limits_0^1 {{{\left( {2x + m} \right)}^{ - \frac{1}{2}}}dx} = \dfrac{1}{2}\left. {\dfrac{{{{\left( {2x + m} \right)}^{\frac{1}{2}}}}}{{\dfrac{1}{2}}}} \right|} _0^1 = \sqrt {2 + m} - \sqrt m \) Từ đề bài ta có \(I \ge 1 \Leftrightarrow \sqrt {2 + m} - \sqrt m \ge 1\) \(\left( {m > 0} \right)\) \(\sqrt {2 + m} \ge \sqrt m + 1 \Leftrightarrow 2 + m \ge m + 2\sqrt m + 1 \Leftrightarrow 2\sqrt m \le 1 \Leftrightarrow m \le \dfrac{1}{4} \Rightarrow 0 < m \le \dfrac{1}{4}.\) Chọn A Câu hỏi 12 : Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), thỏa mãn \(f\left( {{x^5} + 4x + 3} \right) = 2x + 1\) với mọi \(x \in \mathbb{R}\). Tích phân \(\int\limits_{ - 2}^8 {f\left( x \right)dx} \) bằng:
Đáp án: A Phương pháp giải: Đặt \({x^5} + 4x + 3 = t\). Lời giải chi tiết: Đặt \({x^5} + 4x + 3 = t \Rightarrow \left( {5{x^4} + 4} \right)dx = dt\) Giải phương trình: \({x^5} + 4x + 3 = - 2 \Leftrightarrow x = - 1\) \({x^5} + 4x + 3 = 8 \Leftrightarrow x = 1\) Ta có: \(f\left( {{x^5} + 4x + 3} \right) = 2x + 1 \Rightarrow \left( {5{x^4} + 4} \right).f\left( {{x^5} + 4x + 3} \right) = \left( {5{x^4} + 4} \right)\left( {2x + 1} \right)\) \( \Rightarrow \int\limits_{ - 1}^1 {\left( {5{x^4} + 4} \right).f\left( {{x^5} + 4x + 3} \right)dx} = \int\limits_{ - 1}^1 {\left( {5{x^4} + 4} \right)\left( {2x + 1} \right)} dx \Leftrightarrow \int\limits_{ - 2}^8 {f\left( t \right)dt} = \int\limits_{ - 1}^1 {\left( {10{x^5} + 5{x^4} + 8x + 4} \right)} dx\) Chọn: A Câu hỏi 13 : Biết \(\int\limits_1^3 {\dfrac{{\left( {3x + 1} \right)dx}}{{3{x^2} + x\ln x}}} = \ln \left( {a + \dfrac{{\ln b}}{c}} \right)\) với \(a,b,c\) là các số nguyên dương và \(c \le 4\). Tổng \(a + b + c\) bằng :
Đáp án: D Phương pháp giải: Đặt \(t = \ln x \Rightarrow x = {e^t} \Rightarrow dx = {e^t}dt\). Lời giải chi tiết: Đặt \(t = \ln x \Rightarrow x = {e^t} \Rightarrow dx = {e^t}dt\). Đổi cận \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 0\\x = 3 \Rightarrow t = \ln 3\end{array} \right.\). \(\begin{array}{l} \Rightarrow \int\limits_1^3 {\dfrac{{\left( {3x + 1} \right)dx}}{{3{x^2} + x\ln x}}} = \int\limits_0^{\ln 3} {\dfrac{{\left( {3{e^t} + 1} \right){e^t}dt}}{{3{e^{2t}} + {e^t}t}}} = \int\limits_0^{\ln 3} {\dfrac{{3{e^t} + 1dt}}{{3{e^t} + t}}} = \int\limits_0^{\ln 3} {\dfrac{{d\left( {3{e^t} + t} \right)}}{{3{e^t} + t}}} \\ = \left. {\ln \left| {3{e^t} + t} \right|} \right|_0^{\ln 3} = \ln \left| {9 + \ln 3} \right| - \ln 3 = \ln \dfrac{{9 + \ln 3}}{3} = \ln \left( {3 + \dfrac{{\ln 3}}{3}} \right) \Rightarrow \left\{ \begin{array}{l}a = 3\\b = 3\\c = 3\,\,\left( {tm} \right)\end{array} \right. \Rightarrow a + b + c = 9\end{array}\) Chọn D. Câu hỏi 14 : Một người lái xe ô tô đang chạy với vận tốc \(20m/s\) thì người lái xe phát hiện có hàng rào ngăn đường ở phía trước cách 45m( tính từ vị trí đầu xe đến hàng rào)vì vậy, người lái xe đạp phanh. Từ thời điểm đó xe chuyển động chậm dần đều với vận tốc \(v(t) = - 5t + 20(m/s)\), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, xe ô tô còn cách hàng rào ngăn cách bao nhiêu mét( tính từ vị trí đầu xe đến hàng rào)?
Đáp án: A Phương pháp giải: - Tính thời gian ô tô đi được đến lúc dừng hẳn. - Tính quãng đường ô tô đi được đến lúc dừng hẳn \(S = \int\limits_a^b {v\left( t \right)dt} \). - Tính khoảng cách từ đầu xe đến hàng rào. Lời giải chi tiết: Khi xe dừng hẳn thì \(v = 0 \Rightarrow - 5t + 20 = 0 \Leftrightarrow t = 4s\). Quãng đường ô tô đi được trong \(4s\) là : \(S = \int\limits_0^4 {\left( { - 5t + 20} \right)dt} = \left. {\left( { - \dfrac{{5{t^2}}}{2} + 20t} \right)} \right|_0^4 = 40m\). Xe ô tô còn cách hàng rào: \(45 - 40 = 5m\). Chọn A Câu hỏi 15 : Cho \(I = \int\limits_0^{ - 1} {x{{(x - 1)}^2}dx} \) khi đặt \(t = - x\) ta có :
Đáp án: D Phương pháp giải: Sử dụng phương pháp đổi biến số Lời giải chi tiết: Đặt \(t = - x \Rightarrow dt = - dx \Leftrightarrow dx = - dt\) Đổi cận \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = - 1 \Rightarrow t = 1\end{array} \right.\) Khi đó \(I = \int\limits_0^{ - 1} {x{{(x - 1)}^2}dx} = \int\limits_0^1 {\left( { - t} \right){{\left( { - t - 1} \right)}^2}\left( { - dt} \right)} = \int\limits_0^1 {t{{\left( {t + 1} \right)}^2}dt} \) Chọn D Câu hỏi 16 : Cho \(\int\limits_1^3 {\frac{{2x + 1}}{{{x^2} + 3x + 2}}dx = a\ln 2 + b\ln 3 + c\ln 5,} \) với \(a,\,\,b,\,\,c \in \mathbb{Z}.\) Giá trị của \(a + b + c\) bằng:
Đáp án: A Phương pháp giải: Tính tích phân bằng phương pháp tính tích phân của hàm số hữu tỉ rồi suy ra các giá trị của \(a,\,b,\,c\) rồi tính giá trị của biểu thức và chọn đáp án đúng. Lời giải chi tiết: Ta có: \(\eqalign{ Chọn A. Câu hỏi 17 : Cho hàm số \(f\left( x \right)\) không âm, có đạo hàm trên đoạn \(\left[ {0;1} \right]\) và thỏa mãn \(f\left( 1 \right) = 1,\)\(\left[ {2f\left( x \right) + 1 - {x^2}} \right]f'\left( x \right) = 2x\left[ {1 + 2f\left( x \right)} \right]\) , \(\forall x \in \left[ {0;1} \right]\). Tích phân \(\int\limits_0^1 {f\left( x \right)dx} \) bằng
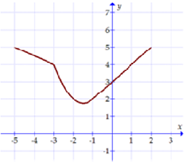
Đáp án: C Phương pháp giải: Biến đổi rồi lấy nguyên hàm hai vế , từ đó tìm ra hàm \(f\left( x \right)\) rồi tính tích phân. Chú ý \(\int {f'\left( x \right)dx} = f\left( x \right) + C\). Lời giải chi tiết: Ta có \(\left[ {2f\left( x \right) + 1 - {x^2}} \right]f'\left( x \right) = 2x\left[ {1 + f\left( x \right)} \right]\) \(\begin{array}{l} \Leftrightarrow 2f\left( x \right).f'\left( x \right) + f'\left( x \right)\left( {1 - {x^2}} \right) = 2x.\left( {1 + f\left( x \right)} \right)\\ \Leftrightarrow 2f\left( x \right).f'\left( x \right) = \left( {{x^2} - 1} \right)f'\left( x \right) + 2x\left( {1 + f\left( x \right)} \right)\\ \Leftrightarrow {\left[ {{f^2}\left( x \right)} \right]^\prime } = {\left[ {\left( {{x^2} - 1} \right)\left( {f\left( x \right) + 1} \right)} \right]^\prime }\end{array}\) Lấy nguyên hàm hai vế ta được \({f^2}\left( x \right) = \left( {{x^2} - 1} \right)\left( {f\left( x \right) + 1} \right) + C\) Lại có \(f\left( 1 \right) = 1 \Rightarrow 1 = \left( {1 - 1} \right).2 + C \Rightarrow C = 1\) Nên \({f^2}\left( x \right) = \left( {{x^2} - 1} \right)\left( {f\left( x \right) + 1} \right) + 1\) \(\begin{array}{l} \Leftrightarrow {f^2}\left( x \right) = {x^2}f\left( x \right) + {x^2} - f\left( x \right)\\ \Leftrightarrow f\left( x \right)\left( {{x^2} - f\left( x \right)} \right) + {x^2} - f\left( x \right) = 0\\ \Leftrightarrow \left( {{x^2} - f\left( x \right)} \right)\left( {f\left( x \right) + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = - 1\left( {ktm} \right)\\f\left( x \right) = {x^2}\left( {tm} \right)\end{array} \right.\end{array}\) Suy ra \(\int\limits_0^1 {f\left( x \right)dx} = \int\limits_0^1 {{x^2}dx} = \dfrac{1}{3}.\) Chọn C Câu hỏi 18 : Cho hàm số \(f\left( x \right)\) liên tục có đồ thị như hình bên dưới. Biết \(F'\left( x \right) = f\left( x \right),\,\forall x \in \left[ { - 5;2} \right]\) và \(\int\limits_{ - 3}^{ - 1} {f\left( x \right)dx} = \frac{{14}}{3}\). Tính \(F\left( 2 \right) - F\left( { - 5} \right)\).
Đáp án: D Phương pháp giải: Tính tích phân trên từng khoảng của các hàm số. Lời giải chi tiết: \(F\left( 2 \right) - F\left( { - 5} \right) = \int\limits_{ - 5}^2 {f\left( x \right)dx} = \int\limits_{ - 5}^{ - 3} {\frac{{5 - x}}{2}dx} + \int\limits_{ - 3}^{ - 1} {f\left( x \right)dx} + \int\limits_{ - 1}^2 {f\left( {x + 3} \right)dx} = \frac{{145}}{6}\). Chọn: D Câu hỏi 19 : Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 1} \right)\left( {{x^2} - 3} \right)\left( {{x^4} - 1} \right)\) với mọi \(x\) thuộc \(\mathbb{R}.\) So sánh \(f\left( { - 2} \right),f\left( 0 \right),f\left( 2 \right)\) ta được
Đáp án: C Phương pháp giải: Lời giải chi tiết: Sử dụng MTCT ta tính được: \(\int\limits_{ - 2}^0 {f'\left( x \right)dx} = \int\limits_{ - 2}^0 {\left( {x - 1} \right)\left( {{x^2} - 3} \right)\left( {{x^4} - 1} \right)} < 0\) \( \Rightarrow f\left( 0 \right) - f\left( { - 2} \right) < 0 \Leftrightarrow f\left( 0 \right) < f\left( { - 2} \right)\,\,\left( 1 \right)\) \(\eqalign{ Từ (1) và (2) ta có: \(f\left( 2 \right) < f\left( 0 \right) < f\left( { - 2} \right).\) Chọn C. Câu hỏi 20 : Cho hàm số \(f\left( x \right)\) thoả mãn \(\int\limits_0^3 {\left[ {2x\ln \left( {x + 1} \right) + xf'\left( x \right)} \right]dx = 0} \) và \(f\left( 3 \right) = 1.\) Biết \(\int\limits_0^3 {f\left( x \right)dx = } \frac{{a + b\ln 2}}{2}\) với \(a,b\) là các số thực dương. Giá trị của \(a + b\) bằng
Đáp án: A Phương pháp giải: - Tách tích phân đã cho thành hai tích phân nhỏ. - Tính mỗi tích phân này bằng phương pháp từng phần. Từ đó suy ra tích phân cần tính giá trị và suy ra \(a,b\). Lời giải chi tiết: \(\int\limits_0^3 {\left[ {2x\ln \left( {x + 1} \right) + xf'\left( x \right)} \right]dx = 0} \)\( \Leftrightarrow \int\limits_0^3 {\left[ {2x\ln \left( {x + 1} \right)} \right]dx} + \int\limits_0^3 {xf'\left( x \right)dx} = 0\) +) Tính \(I = \int\limits_0^3 {\left[ {2x\ln \left( {x + 1} \right)} \right]dx} \). Đặt \(\left\{ \begin{array}{l}u = \ln \left( {x + 1} \right)\\dv = 2xdx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{{dx}}{{x + 1}}\\v = {x^2}\end{array} \right.\) \(\begin{array}{l} \Rightarrow I = \left. {{x^2}\ln \left( {x + 1} \right)} \right|_0^3 - \int\limits_0^3 {\frac{{{x^2}}}{{x + 1}}dx} = 9\ln 4 - \int\limits_0^3 {\left( {x - 1 + \frac{1}{{x + 1}}} \right)dx} \\ = 18\ln 2 - \left. {\left( {\frac{{{x^2}}}{2} - x + \ln \left| {x + 1} \right|} \right)} \right|_0^3 = 18\ln 2 - \frac{3}{2} - \ln 4 = 16\ln 2 - \frac{3}{2} \Rightarrow I = 16\ln 2 - \frac{3}{2}\end{array}\) +) Tính \(J = \int\limits_0^3 {xf'\left( x \right)dx} \). Đặt \(\left\{ \begin{array}{l}u = x\\dv = f'\left( x \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = f\left( x \right)\end{array} \right.\). \( \Rightarrow J = \left. {xf\left( x \right)} \right|_0^3 - \int\limits_0^3 {f\left( x \right)dx} = 3f\left( 3 \right) - \int\limits_0^3 {f\left( x \right)dx} = 3 - \int\limits_0^3 {f\left( x \right)dx} \). \( \Rightarrow I + J = 0 \Leftrightarrow 16\ln 2 - \frac{3}{2} + 3 - \int\limits_0^3 {f\left( x \right)dx} = 0 \Rightarrow \int\limits_0^3 {f\left( x \right)dx} = 16\ln 2 - \frac{3}{2} + 3 = \frac{{3 + 32\ln 2}}{2}\). Do đó \(a = 3,b = 32 \Rightarrow a + b = 35\). Chọn A. Câu hỏi 21 : Biết \(f(x)\) là hàm liên tục trên \(\mathbb{R}\) và \(\int\limits_0^{\dfrac{\pi }{2}} {f(x)dx = 4} \). Khi đó \(\int\limits_0^{\dfrac{\pi }{4}} {\left[ {f(2x) - {\mathop{\rm s}\nolimits} {\rm{inx}}} \right]} dx\) bằng:
Đáp án: D Phương pháp giải: - Tách tích phân cần tính thành hai tích phân. - Tính các tích phân có được bằng cách sử dụng tích phân cơ bản và phương pháp đổi biến tính tích phân. Lời giải chi tiết: Ta có: \(\int\limits_0^{\dfrac{\pi }{4}} {\left[ {f(2x) - \sin x} \right]} dx = \int\limits_0^{\dfrac{\pi }{4}} {f\left( {2x} \right)} dx - \int\limits_0^{\dfrac{\pi }{4}} {\sin x} dx = I - J\) Tính \(I = \int\limits_0^{\dfrac{\pi }{4}} {f\left( {2x} \right)dx} \). Đặt \(t = 2x \Rightarrow dt = 2dx\)\( \Rightarrow I = \int\limits_0^{\dfrac{\pi }{2}} {f\left( t \right).\dfrac{{dt}}{2}} = \dfrac{1}{2}\int\limits_0^{\dfrac{\pi }{2}} {f\left( t \right)dt} = \dfrac{1}{2}.4 = 2\). Tính \(J = \int\limits_0^{\dfrac{\pi }{4}} {\sin x} dx = - \left. {\cos x} \right|_0^{\dfrac{\pi }{4}} = - \left( {\dfrac{{\sqrt 2 }}{2} - 1} \right) = 1 - \dfrac{{\sqrt 2 }}{2}\). Vậy \(I - J = 2 - \left( {1 - \dfrac{{\sqrt 2 }}{2}} \right) = 1 + \dfrac{{\sqrt 2 }}{2}\) hay \(\int\limits_0^{\dfrac{\pi }{4}} {\left[ {f(2x) - \sin x} \right]} dx = 1 + \dfrac{{\sqrt 2 }}{2}\). Chọn D Câu hỏi 22 : Biết \(I = \int\limits_1^e {{x^2}\ln xdx} = a{e^3} + b\) với \(a,b\) là các số hữu tỉ. Giá trị của \(9\left( {a + b} \right)\) bằng
Đáp án: A Phương pháp giải: - Sử dụng tích phân từng phần, đặt \(\left\{ \begin{array}{l}u = \ln x\\dx = {x^2}dx\end{array} \right.\). - Tính tích phân đã cho tìm \(a,b\) và kết luận. Lời giải chi tiết: Đặt \(\left\{ \begin{array}{l}u = \ln x\\dx = {x^2}dx\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}du = \dfrac{1}{x}dx\\v = \dfrac{{{x^3}}}{3}\end{array} \right.\) \( \Rightarrow I = \left. {\left( {\dfrac{{{x^3}}}{3}\ln x} \right)} \right|_1^e - \int\limits_1^e {\left( {\dfrac{{{x^3}}}{3}.\dfrac{1}{x}} \right)dx} = \dfrac{{{e^3}}}{3} - \dfrac{1}{3}\int\limits_1^e {{x^2}dx} = \dfrac{{{e^3}}}{3} - \left. {\dfrac{1}{3}.\dfrac{{{x^3}}}{3}} \right|_1^e = \dfrac{{{e^3}}}{3} - \dfrac{{{e^3}}}{9} + \dfrac{1}{9} = \dfrac{2}{9}{e^3} + \dfrac{1}{9}\) \( \Rightarrow a = \dfrac{2}{9},b = \dfrac{1}{9} \Rightarrow 9\left( {a + b} \right) = 3\). Chọn A. Câu hỏi 23 : Biết \(\int\limits_1^2 {\frac{{\ln x}}{{{x^2}}}{\rm{d}}x} = a\ln 2 + \frac{b}{c}\) (với \(a\) là số hữu tỉ, \(b\), \(c\) là các số nguyên dương và \(\frac{b}{c}\) là phân số tối giản). Tính giá trị của \(S = 2a + 3b + c\).
Đáp án: A Phương pháp giải: Sử dụng phương pháp đổi biến và nguyên hàm từng phần để để tính tích phân và chọn đáp án đúng. Lời giải chi tiết: Ta có: \(I = \int\limits_1^2 {\dfrac{{\ln x}}{{{x^2}}}} dx\) Đặt \(\ln x = t \Rightarrow x = {e^t} \Rightarrow dt = \dfrac{1}{x}dx\). Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 0\\x = 2 \Rightarrow t = \ln 2\end{array} \right..\) \( \Rightarrow I = \int\limits_0^{\ln 2} {\dfrac{t}{{{e^t}}}dt = } \int\limits_0^{\ln 2} {t{e^{ - t}}dt} \) Đặt: \(\left\{ \begin{array}{l}u = t\\dv = {e^{ - t}}dt\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dt\\v = - {e^{ - t}}\end{array} \right.\) \(\begin{array}{l} \Rightarrow I = \left. { - t{e^{ - t}}} \right|_0^{\ln 2} + \int\limits_0^{\ln 2} {{e^{ - t}}dt} = - \ln 2.{e^{ - \ln 2}} - \left. {{e^{ - t}}} \right|_0^{\ln 2} = - \dfrac{1}{2}\ln 2 - {e^{ - \ln 2}} + 1 = - \dfrac{1}{2}\ln 2 + \dfrac{1}{2}.\\ \Rightarrow \left\{ \begin{array}{l}a = - \dfrac{1}{2}\\b = 1\\c = 2\end{array} \right. \Rightarrow S = 2a + 3b + c = 4.\end{array}\) Chọn A. Câu hỏi 24 : Cho \(\int\limits_1^2 {\left( {x + 1} \right){e^x}dx} = a{e^2} + be + c\) với \(a,b,c\) là các số nguyên. Tính \(a + b + c\).
Đáp án: B Phương pháp giải: Thực hiện tích phân từng phần: Đặt \(\left\{ \begin{array}{l}u = x + 1\\dv = {e^x}dx\end{array} \right.\) tính tích phân đã cho suy ra \(a,b,c\) và kết luận. Lời giải chi tiết: Đặt \(\left\{ \begin{array}{l}u = x + 1\\dv = {e^x}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = {e^x}\end{array} \right.\) \(\begin{array}{l} \Rightarrow \int\limits_1^2 {\left( {x + 1} \right){e^x}dx} = \left. {\left( {x + 1} \right){e^x}} \right|_1^2 - \int\limits_1^2 {{e^x}dx} = 3{e^2} - 2e - \left. {{e^x}} \right|_1^2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{e^2} - 2e - {e^2} + e = 3{e^2} - {e^2} - e\end{array}\) Vậy \(a = 3,b = - 1,c = - 1 \Rightarrow a + b + c = 1\). Chọn B. Câu hỏi 25 : Biết \(\int\limits_2^{e + 1} {\dfrac{{\ln \left( {x - 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}dx = a + b{e^{ - 1}}} \) với \(a,b \in \mathbb{Z}.\) Chọn khẳng định đúng trong các khẳng định sau:
Đáp án: B Phương pháp giải: Sử dụng phương pháp tích phân từng phần với \(\left\{ \begin{array}{l}\ln \left( {x - 1} \right) = u\\\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}dx = dv\end{array} \right.\) Lời giải chi tiết: Đặt \(\left\{ \begin{array}{l}\ln \left( {x - 1} \right) = u\\\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}dx = dv\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{{x - 1}}dx = du\\ - \dfrac{1}{{x - 1}} = v\end{array} \right.\) Ta có \(\int\limits_2^{e + 1} {\dfrac{{\ln \left( {x - 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}dx = \ln \left( {x - 1} \right).\left. {\left( { - \dfrac{1}{{x - 1}}} \right)} \right|} _2^{e + 1} + \int\limits_2^{e + 1} {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}dx} \) \( = - \dfrac{1}{e} - \left. {\dfrac{1}{{x - 1}}} \right|_2^{e + 1} = - \dfrac{1}{e} - \dfrac{1}{e} + 1 = 1 - 2.{e^{ - 1}}\) Suy ra \(a = 1;\,\,\,b = - 2 \Rightarrow a + b = - 1.\) Chọn B. Câu hỏi 26 : \(\int\limits_0^1 {\left( {1 + 3x} \right)f'\left( x \right)dx} = 2019;\,4f\left( 1 \right) - f\left( 0 \right) = 2020.\) Tính \(\int\limits_0^{\frac{1}{3}} {f\left( {3x} \right)dx.} \)
Đáp án: A Phương pháp giải: Sử dụng phương pháp tích phân từng phần và đổi biến số. Lời giải chi tiết: Xét \(\int\limits_0^1 {\left( {1 + 3x} \right)f'\left( x \right)dx} = 2019\) Đặt \(\left\{ \begin{array}{l}1 + 3x = u\\f'\left( x \right)dx = dv\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3dx = du\\f\left( x \right) = v\end{array} \right.\) Suy ra \(\int\limits_0^1 {\left( {1 + 3x} \right)f'\left( x \right)dx} = \left. {\left( {1 + 3x} \right)f\left( x \right)} \right|_0^1 - 3\int\limits_0^1 {f\left( x \right)dx} \) \( = 4f\left( 1 \right) - f\left( 0 \right) - 3\int\limits_0^1 {f\left( x \right)dx} = 2020 - 3\int\limits_0^1 {f\left( x \right)dx} = 2019\) \( \Leftrightarrow \int\limits_0^1 {f\left( x \right)dx} = \dfrac{1}{3}\) Xét \(\int\limits_0^{\frac{1}{3}} {f\left( {3x} \right)dx} \), đặt \(3x = t \Leftrightarrow 3dx = dt \Leftrightarrow dx = \dfrac{{dt}}{3}\). Đổi cận : \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = \dfrac{1}{3} \Rightarrow t = 1\end{array} \right.\). Suy ra \(\int\limits_0^{\frac{1}{3}} {f\left( {3x} \right)dx} = \dfrac{1}{3}\int\limits_0^1 {f\left( t \right)dt} = \dfrac{1}{3}.\int\limits_0^1 {f\left( x \right)dx} = \dfrac{1}{3}.\dfrac{1}{3} = \dfrac{1}{9}\) Chọn A. Câu hỏi 27 : Cho hàm số \(y = f\left( x \right)\) với \(f\left( 0 \right) = f\left( 1 \right) = 1.\) Biết rằng: \(\int\limits_0^1 {{e^x}\left[ {f\left( x \right) + f'\left( x \right)} \right]dx = ae + b,} \) \(a,b \in \mathbb{Z}.\) Giá trị biểu thức \({a^{2019}} + {b^{2019}}\) bằng
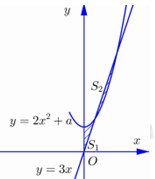
Đáp án: C Phương pháp giải: \(\int\limits_a^b {f'\left( x \right)dx = \left. {f\left( x \right)} \right|_a^b} .\) Lời giải chi tiết: \(\begin{array}{l}\int\limits_0^1 {{e^x}\left[ {f\left( x \right) + f'\left( x \right)} \right]dx} = \int\limits_0^1 {\left[ {{e^x}f\left( x \right) + {e^x}f'\left( x \right)} \right]dx} \\ = \int\limits_0^1 {\left[ {{e^x}f\left( x \right)} \right]'dx} = \left. {\left[ {{e^x}f\left( x \right)} \right]} \right|_0^1 = e.f\left( 1 \right) - f\left( 0 \right) = e - 1\\ \Rightarrow a = 1;\,\,\,b = - 1 \Rightarrow {a^{2019}} + {b^{2019}} = {1^{2019}} + {\left( { - 1} \right)^{2019}} = 1 - 1 = 0\end{array}\) Chọn: C Câu hỏi 28 : Cho đường thẳng \(y = 3x\) và parabol \(y = 2{x^2} + a\) (\(a\) là tham số thực dương). Gọi \({S_1}\) và \({S_2}\) lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi \({S_1} = {S_2}\) thì \(a\) thuộc khoảng nào dưới đây?
Đáp án: A Phương pháp giải: - Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình có hai nghiệm phân biệt. - Viết công thức tính hai phần diện tích \({S_1},{S_2}\). - Sử dụng điều kiện \({S_1} = {S_2}\) tìm \(a\). Lời giải chi tiết: Phương trình hoành độ giao điểm : \(2{x^2} + a = 3x \Leftrightarrow 2{x^2} - 3x + a = 0\). Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta = 9 - 8a > 0 \Leftrightarrow a < \dfrac{9}{8}\). Khi đó phương trình có hai nghiệm phân biệt \({x_1} < {x_2}\). Ta có : \({S_1} = \int\limits_0^{{x_1}} {\left( {2{x^2} + a - 3x} \right)dx} = \left. {\left( {\dfrac{2}{3}{x^3} - \dfrac{3}{2}{x^2} + ax} \right)} \right|_0^{{x_1}} = \dfrac{2}{3}x_1^3 - \dfrac{3}{2}x_1^2 + a{x_1}\) \({S_2} = \int\limits_{{x_1}}^{{x_2}} {\left( {3x - 2{x^2} - a} \right)dx} = \left. {\left( {\dfrac{3}{2}{x^2} - \dfrac{2}{3}{x^3} - ax} \right)} \right|_{{x_1}}^{{x_2}} = \dfrac{3}{2}x_2^2 - \dfrac{2}{3}x_2^3 - a{x_2} - \dfrac{3}{2}x_1^2 + \dfrac{2}{3}x_1^3 + a{x_1}\) Do \({S_1} = {S_2}\) nên \(\dfrac{2}{3}x_1^3 - \dfrac{3}{2}x_1^2 + a{x_1} = \dfrac{3}{2}x_2^2 - \dfrac{2}{3}x_2^3 - a{x_2} - \dfrac{3}{2}x_1^2 + \dfrac{2}{3}x_1^3 + a{x_1}\) \( \Leftrightarrow \dfrac{3}{2}x_2^2 - \dfrac{2}{3}x_2^3 - a{x_2} = 0 \Leftrightarrow 9x_2^2 - 4x_2^3 - 6a{x_2} = 0\,\,\left( 1 \right)\) Lại có \(2x_2^2 - 3{x_2} + a = 0 \Leftrightarrow a = 3{x_2} - 2x_2^2\) thay vào \(\left( 1 \right)\) được : \(9x_2^2 - 4x_2^3 - 6\left( {3{x_2} - 2x_2^2} \right){x_2} = 0 \Leftrightarrow 8x_2^3 - 9x_2^2 = 0 \Leftrightarrow \left[ \begin{array}{l}{x_2} = 0 \Rightarrow a = 0\left( {KTM} \right)\\{x_2} = \dfrac{9}{8} \Rightarrow a = \dfrac{{27}}{{32}}\left( {TM} \right)\end{array} \right.\) Vậy \(a = \dfrac{{27}}{{32}} \in \left( {\dfrac{4}{5};\dfrac{9}{{10}}} \right)\). Chọn A. Câu hỏi 29 : Cho hàm số \(f\left( x \right)\). Biết \(f\left( 0 \right) = 4\) và \(f'\left( x \right) = 2{\sin ^2}x + 3\), \(\forall x \in \mathbb{R}\), khi đó \(\int\limits_0^{\dfrac{\pi }{4}} {f\left( x \right)} dx\) bằng
Đáp án: C Phương pháp giải: +) Tính \(f\left( x \right) = \int {f'\left( x \right)dx} \). +) Sử dụng các công thức nguyên hàm cơ bản để tính \(\int\limits_0^{\dfrac{\pi }{4}} {f\left( x \right)} dx\). Lời giải chi tiết: Ta có \(f'\left( x \right) = 2{\sin ^2}x + 3 = 1 - \cos 2x + 3 = 4 - \cos 2x\). \( \Rightarrow f\left( x \right) = \int {f'\left( x \right)dx} = \int {\left( {4 - \cos 2x} \right)dx} = 4x - \dfrac{1}{2}\sin 2x + C\) Theo giả thiết có \(f\left( 0 \right) = 4 \Leftrightarrow 4.0 - \dfrac{1}{2}\sin 0 + C = 4 \Leftrightarrow C = 4\). \(\begin{array}{l} \Rightarrow f\left( x \right) = 4x - \dfrac{1}{2}\sin 2x + 4\\ \Rightarrow \int\limits_0^{\dfrac{\pi }{4}} {f\left( x \right)dx} = \int\limits_0^{\dfrac{\pi }{4}} {\left( {4x - \dfrac{1}{2}\sin 2x + 4} \right)dx} \\ = \left. {\left( {2{x^2} + \dfrac{1}{4}\cos 2x + 4x} \right)} \right|_0^{\dfrac{\pi }{4}} = 2\dfrac{{{\pi ^2}}}{{16}} + \pi - \dfrac{1}{4} = \dfrac{{{\pi ^2} + 8\pi - 2}}{8}\end{array}\). Chọn C Câu hỏi 30 : Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Biết \(f\left( 6 \right) = 1\) và \(\int\limits_0^1 {xf\left( {6x} \right)dx} = 1\), khi đó \(\int\limits_0^6 {{x^2}f'\left( x \right)dx} \) bằng
Đáp án: D Phương pháp giải: Sử dụng kết hợp các phương pháp đổi biến và từng phần để tính tích phân. Lời giải chi tiết: Đặt \(t = 6x \Rightarrow dt = 6dx \Rightarrow dx = \dfrac{{dt}}{6}\). Khi đó \(1 = \int\limits_0^1 {xf\left( {6x} \right)dx} = \int\limits_0^6 {\dfrac{1}{6}t.f\left( t \right).\dfrac{{dt}}{6}} = \dfrac{1}{{36}}\int\limits_0^6 {t.f\left( t \right)dt} \) \( \Rightarrow \int\limits_0^6 {xf\left( x \right)dx} = 1.36 = 36\). Đặt \(\left\{ \begin{array}{l}{x^2} = u\\f'\left( x \right)dx = dv\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = 2xdx\\v = f\left( x \right)\end{array} \right.\) \( \Rightarrow \int\limits_0^6 {{x^2}f'\left( x \right)dx} = \left. {{x^2}f\left( x \right)} \right|_0^6 - \int\limits_0^6 {2xf\left( x \right)dx} = 36f\left( 6 \right) - 2\int\limits_0^6 {xf\left( x \right)dx} = 36.1 - 2.36 = - 36\). Chọn D. Câu hỏi 31 : Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Biết \(f\left( 5 \right) = 1\) và \(\int\limits_0^1 {xf\left( {5x} \right){\rm{d}}x} = 1\), khi đó \(\int\limits_0^5 {{x^2}f'\left( x \right){\rm{d}}x} \) bằng
Đáp án: D Phương pháp giải: Sử dụng phương pháp đổi biến số và tích phân từng phần Lưu ý rằng tích phân không phụ thuộc vào biến Lời giải chi tiết: Đặt \(t = 5x \Rightarrow \left\{ \begin{array}{l}dx = \dfrac{{dt}}{5}\\x = \dfrac{t}{5}\end{array} \right.\). Đổi cận: Với \(x = 0 \Rightarrow t = 0\); với \(x = 1 \Rightarrow t = 5\). Khi đó: \(\int\limits_0^1 {xf\left( {5x} \right){\rm{d}}x} = 1 \Leftrightarrow \int\limits_0^5 {\dfrac{t}{5}f\left( t \right)\dfrac{{{\rm{dt}}}}{5}} = 1 \Leftrightarrow \int\limits_0^5 {t.f\left( t \right){\rm{d}}t} = 25\) Do đó \(\int\limits_0^5 {x.f\left( x \right){\rm{d}}x} = 25\,\) (vì tích phân không phụ thuộc vào biến) Đặt: \(\left\{ \begin{array}{l}u = f\left( x \right)\\{\rm{d}}v = x{\rm{d}}x\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\rm{d}}u = f'\left( x \right){\rm{d}}x\\v = \dfrac{{{x^2}}}{2}\end{array} \right.\). Ta có: \(\int\limits_0^5 {x.f\left( x \right){\rm{d}}x} = 25\, \Leftrightarrow \dfrac{{{x^2}}}{2}.f\left( x \right)\left| \begin{array}{l}5\\0\end{array} \right. - \dfrac{1}{2}\int\limits_0^5 {{x^2}.f'\left( x \right){\rm{d}}x} = 25\) \( \Leftrightarrow \dfrac{{25}}{2} - \dfrac{1}{2}\int\limits_0^5 {{x^2}.f'\left( x \right){\rm{d}}x} = 25 \Leftrightarrow \int\limits_0^5 {{x^2}.f'\left( x \right){\rm{d}}x} = - 25\). Chọn D. Câu hỏi 32 : Tính tích phân \(I = \int\limits_{ - 2}^0 {\left| {\dfrac{{{x^2} - x - 2}}{{x - 1}}} \right|dx} \) ta được kết quả \(I = a + b\ln 2 + c\ln 3\) (với \(a,\,\,b,\,\,c\) là các số nguyên). Khi đó giá trị của biểu thức \(T = {a^3} + 3{b^2} + 2c\) là:
Đáp án: C Phương pháp giải: - Xét dấu biểu thức \(\dfrac{{{x^2} - x - 2}}{{x - 1}}\) sau đó chia các khoảng để phá trị tuyệt đối. - Sử dụng phương pháp tính tích phân hàm hữu tỉ khi bậc tử > bậc mẫu (chia tử cho mẫu). - Sử dụng các nguyên hàm cơ bản để tính tích phân. Lời giải chi tiết: Ta có: \(\dfrac{{{x^2} - x - 2}}{{x - 1}} = \dfrac{{\left( {x + 1} \right)\left( {x - 2} \right)}}{{x - 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\). Ta có bảng xét dấu:
Khi đó ta có: \(\begin{array}{l}I = \int\limits_{ - 2}^0 {\left| {\dfrac{{{x^2} - x - 2}}{{x - 1}}} \right|dx} \\\,\,\,\, = \int\limits_{ - 2}^{ - 1} {\left| {\dfrac{{{x^2} - x - 2}}{{x - 1}}} \right|dx} + \int\limits_{ - 1}^0 {\left| {\dfrac{{{x^2} - x - 2}}{{x - 1}}} \right|dx} \\\,\,\,\, = - \int\limits_{ - 2}^{ - 1} {\dfrac{{{x^2} - x - 2}}{{x - 1}}dx} + \int\limits_{ - 1}^0 {\dfrac{{{x^2} - x - 2}}{{x - 1}}dx} \\\,\,\,\, = - \int\limits_{ - 2}^{ - 1} {\left( {x - \dfrac{2}{{x - 1}}} \right)dx} + \int\limits_{ - 1}^0 {\left( {x - \dfrac{2}{{x - 1}}} \right)dx} \\\,\,\,\, = - \left. {\left( {\dfrac{{{x^2}}}{2} - 2\ln \left| {x - 1} \right|} \right)} \right|_{ - 2}^{ - 1} + \left. {\left( {\dfrac{{{x^2}}}{2} - 2\ln \left| {x - 1} \right|} \right)} \right|_{ - 1}^0\\\,\,\,\, = - \left( {\dfrac{1}{2} - 2\ln 2} \right) + \left( {2 - 2\ln 3} \right) - \left( {\dfrac{1}{2} - 2\ln 2} \right)\\\,\,\,\, = 1 + 4\ln 2 - 2\ln 3\\ \Rightarrow a = 1,\,\,b = 4,\,\,c = - 2\end{array}\) Vậy \(T = 2{a^3} + 3b - 4c = {2.1^3} + 3.4 - 4\left( { - 2} \right) = 22\). Chọn C. Câu hỏi 33 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Biết \(f\left( {4x} \right) = f\left( x \right) + 4{x^3} + 2x\) và \(f\left( 0 \right) = 2\) . Tính \(\int\limits_0^1 {f\left( x \right)} dx\).
Đáp án: A Phương pháp giải: - Biến đổi đẳng thức đã cho thành: \(f\left( {4x} \right) = f\left( x \right) + 4{x^3} + 2x \Leftrightarrow f\left( {4x} \right) - f\left( x \right) = 4{x^3} + 2x\) - Từ đó suy ra \(f\left( x \right)\) có dạng \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) - Sử dụng điều kiện bài cho tìm hàm số \(f\left( x \right)\) và tính tích phân. Lời giải chi tiết: \(f\left( {4x} \right) = f\left( x \right) + 4{x^3} + 2x \Leftrightarrow f\left( {4x} \right) - f\left( x \right) = 4{x^3} + 2x\) \( \Rightarrow f\left( x \right)\) có dạng \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) Vì \(f\left( 0 \right) = 2 \Rightarrow d = 2\). Ta có: \(\begin{array}{l}f\left( {4x} \right) - f\left( x \right) = 4{x^3} + 2x\\ \Rightarrow \left( {64a{x^3} + 16b{x^2} + 4cx + 2} \right) - \left( {a{x^3} + b{x^2} + cx + 2} \right) = 4{x^3} + 2x\\ \Rightarrow 63a{x^3} + 15b{x^2} + 3cx = 4{x^3} + 2x\\ \Rightarrow \left\{ \begin{array}{l}63a = 4\\15b = 0\\3c = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{4}{{63}}\\b = 0\\c = \dfrac{2}{3}\end{array} \right.\\ \Rightarrow f\left( x \right) = \dfrac{4}{{63}}{x^3} + \dfrac{2}{3}x + 2\end{array}\) Vậy \(\int\limits_0^1 {f\left( x \right)dx} = \int\limits_0^1 {\left( {\dfrac{4}{{63}}{x^3} + \dfrac{2}{3}x + 2} \right)dx} = \dfrac{{148}}{{63}}\). Chọn A. Câu hỏi 34 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(\int\limits_0^7 {f\left( x \right)dx} = 10\) và \(\int\limits_0^3 {f\left( x \right)dx} = 6\). Tính \(I = \int\limits_{ - 2}^3 {f\left| {3 - 2x} \right|dx} \).
Đáp án: D Phương pháp giải: - Tính tích phân bằng phương pháp đổi biến, đặt \(t = 3 - 2x\). - Sử dụng tính chất: \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} \), chia cận phù hợp để phá trị tuyệt đối. Lời giải chi tiết: Đặt \(t = 3 - 2x \Rightarrow dt = - 2dx\). Đổi cận \(\left\{ \begin{array}{l}x = - 2 \Rightarrow t = 7\\x = 3 \Rightarrow t = - 3\end{array} \right.\). Khi đó ta có: \(\begin{array}{l}I = - \dfrac{1}{2}\int\limits_7^{ - 3} {f\left( {\left| t \right|} \right)dt} = \dfrac{1}{2}\int\limits_{ - 3}^7 {f\left( {\left| t \right|} \right)dt} \\\,\,\,\, = \dfrac{1}{2}\left( {\int\limits_{ - 3}^0 {f\left( { - t} \right)dt} + \int\limits_0^7 {f\left( t \right)dt} } \right)\\\,\,\,\, = \dfrac{1}{2}\left( { - \int\limits_3^0 {f\left( x \right)dx} + \int\limits_0^7 {f\left( x \right)dx} } \right)\\\,\,\,\, = \dfrac{1}{2}\left( {\int\limits_0^3 {f\left( x \right)dx} + \int\limits_0^7 {f\left( x \right)dx} } \right)\\\,\,\,\, = \dfrac{1}{2}\left( {6 + 10} \right) = 8\end{array}\). Chọn D. Câu hỏi 35 : Biết \(\int\limits_0^{\dfrac{\pi }{4}} {\dfrac{1}{{1 + \tan x}}dx = a.\pi + b\ln 2} \) với \(a;\,\,b\) là các số hữu tỉ. Tính tỷ số \(\dfrac{a}{b}\).
Đáp án: A Phương pháp giải: Biến đổi hàm số đã cho về \(\dfrac{1}{{1 + \tan x}} = \dfrac{{\cos x}}{{\sin x + \cos x}} = \dfrac{1}{2}\left( {1 + \dfrac{{\cos x - \sin x}}{{\sin x - \cos x}}} \right)\) rồi tính tích phân. Lời giải chi tiết: Ta có : \(\begin{array}{l}\int\limits_0^{\dfrac{\pi }{4}} {\dfrac{1}{{1 + \tan x}}dx} = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{1}{{1 + \dfrac{{\sin x}}{{\cos x}}}}dx} \\ = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{1}{{\dfrac{{\cos x + \sin x}}{{\cos x}}}}dx} = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{\cos x}}{{\sin x + \cos x}}dx} \\ = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{\sin x + \cos x + \cos x - \sin x}}{{2\left( {\sin x + \cos x} \right)}}dx} \\ = \dfrac{1}{2}\int\limits_0^{\dfrac{\pi }{4}} {\left( {1 + \dfrac{{\cos x - \sin x}}{{\sin x + \cos x}}} \right)dx} \\ = \dfrac{1}{2}\left[ {x + \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{d\left( {\sin x + \cos x} \right)}}{{\sin x + \cos x}}} } \right]\\ = \dfrac{1}{2}\left. {\left( {x + \ln \left| {\sin x + \cos x} \right|} \right)} \right|_0^{\dfrac{\pi }{4}}\\ = \dfrac{1}{2}\left( {\dfrac{\pi }{4} + \ln \sqrt 2 } \right) = \dfrac{\pi }{8} + \dfrac{1}{2}\ln \sqrt 2 \\ = \dfrac{\pi }{8} + \dfrac{1}{4}\ln 2\\ \Rightarrow a = \dfrac{1}{8},b = \dfrac{1}{4} \Rightarrow \dfrac{a}{b} = \dfrac{1}{2}\end{array}\) Chọn A. Câu hỏi 36 : Cho \(y = f\left( x \right)\) là một hàm số bất kỳ có đạo hàm trên \(\mathbb{R},\) đặt \(I = \int\limits_0^1 {xf'\left( x \right)dx} .\) Khẳng đinh nào dưới đây đúng?
Đáp án: C Phương pháp giải: Sử dụng phương pháp tích phân từng phần để làm bài. Lời giải chi tiết: Ta có: \(I = \int\limits_0^1 {xf'\left( x \right)dx} \) Đặt \(\left\{ \begin{array}{l}u = x\\dv = f'\left( x \right)dx\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}du = dx\\v = f\left( x \right)\end{array} \right.\) \( \Rightarrow I = \left. {\left[ {xf\left( x \right)} \right]} \right|_0^1 - \int\limits_0^1 {f\left( x \right)dx} \) \( = f\left( 1 \right) + \int\limits_1^0 {f\left( x \right)dx} .\) Chọn C. Câu hỏi 37 : Cho hàm số \(f\left( x \right)\) có \(f\left( 0 \right) = 0\) và \(f'\left( x \right) = {\sin ^4}x\,\,\forall x \in \mathbb{R}\). Tích phân \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} \) bằng:
Đáp án: C Phương pháp giải: - Tìm hàm số \(f\left( x \right) = \int {f'\left( x \right)dx} \). - Sử dụng giả thiết \(f\left( 0 \right) = 0\) tìm hằng số \(C\). - Với hàm \(f\left( x \right)\) tìm được, tính \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} \). Lời giải chi tiết: Ta có \(f\left( x \right) = \int {f'\left( x \right)dx} = \int {{{\sin }^4}xdx} \) \(\begin{array}{l} = \int {{{\left( {\dfrac{{1 - \cos 2x}}{2}} \right)}^2}dx} \\ = \dfrac{1}{4}\int {\left( {1 - 2\cos 2x + {{\cos }^2}2x} \right)dx} \\ = \dfrac{1}{4}\int {\left( {1 - 2\cos 2x + \dfrac{{1 + \cos 4x}}{2}} \right)dx} \\ = \dfrac{1}{4}\left( {x - \sin 2x + \dfrac{1}{2}x + \dfrac{1}{2}.\dfrac{{\sin 4x}}{4}} \right) + C\\ = \dfrac{{3x}}{8} - \dfrac{{\sin 2x}}{4} + \dfrac{{\sin 4x}}{{32}} + C\end{array}\) Theo bài ra ta có \(f\left( 0 \right) = 0 \Leftrightarrow C = 0\) \( \Rightarrow f\left( x \right) = \dfrac{{3x}}{8} - \dfrac{{\sin 2x}}{4} + \dfrac{{\sin 4x}}{{32}}\). Vậy \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} = \int\limits_0^{\frac{\pi }{2}} {\left( {\dfrac{{3x}}{8} - \dfrac{{\sin 2x}}{4} + \dfrac{{\sin 4x}}{{32}}} \right)dx} = \dfrac{{3{\pi ^2} - 16}}{{64}}\) (sử dụng MTCT). Chọn C. Câu hỏi 38 : Cho hàm số \(f\left( x \right)\) là hàm số chẵn và liên tục trên \(\left[ { - 1;1} \right]\) thỏa mãn: \(\int\limits_{ - 1}^1 {f\left( x \right)dx} = \dfrac{{86}}{{15}}\) và \(f\left( 1 \right) = 5\). Khi đó \(\int\limits_0^1 {xf'\left( x \right)dx} \) bằng:
Đáp án: A Phương pháp giải: - Sử dụng tính chất của hàm chẵn: \(\int\limits_{ - a}^a {f\left( x \right)dx} = 2\int\limits_0^a {f\left( x \right)dx} \) (\(f\left( x \right)\) liên tục trên \(\left[ { - a;a} \right]\)). - Sử dụng phương pháp tích phân từng phần \(\int\limits_a^b {udv} = \left. {uv} \right|_a^b - \int\limits_a^b {vdu} \). Lời giải chi tiết: Vì \(f\left( x \right)\) là hàm số chẵn và liên tục trên \(\left[ { - 1;1} \right]\) nên \(\int\limits_{ - 1}^1 {f\left( x \right)dx} = 2\int\limits_0^1 {f\left( x \right)dx} = \dfrac{{86}}{{15}}\) \( \Rightarrow \int\limits_0^1 {f\left( x \right)dx} = \dfrac{{43}}{{15}}\). Xét tích phân \(I = \int\limits_0^1 {xf'\left( x \right)dx} \). Đặt \(\left\{ \begin{array}{l}u = x\\dv = f'\left( x \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = f\left( x \right)\end{array} \right.\), khi đó ta có: \(I = \left. {xf\left( x \right)} \right|_0^1 - \int\limits_0^1 {f\left( x \right)dx} = f\left( 1 \right) - \int\limits_0^1 {f\left( x \right)dx} = 5 - \dfrac{{43}}{{15}} = \dfrac{{32}}{{15}}\). Chọn A. Câu hỏi 39 : Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( 0 \right) = \dfrac{2}{3}\) và \(\left( {\sqrt x + \sqrt {x + 1} } \right)f'\left( x \right) = 1,\,\forall x \ge - 1\). Biết rằng \(\int\limits_0^1 {f\left( x \right)} dx = \dfrac{{a\sqrt 2 + b}}{{15}}\) với \(a,b \in \mathbb{Z}\). Tính \(T = a + b\).
Đáp án: D Phương pháp giải: - Rút \(f'\left( x \right)\) từ giả thiết đề bài cho. - Tìm \(f\left( x \right) = \int {f'\left( x \right)dx} \), sử dụng công thức tính nguyên hàm: \(\int {\sqrt x dx} = \dfrac{2}{3}x\sqrt x + C\). - Từ giả thiết \(f\left( 0 \right) = \dfrac{2}{3}\) tìm hằng số \(C\) và suy ra hàm số \(f\left( x \right)\). - Tính \(\int\limits_0^1 {f\left( x \right)dx} \) với hàm \(f\left( x \right)\) vừa tìm được, đưa kết quả về dạng \(\dfrac{{a\sqrt 2 + b}}{{15}}\). Đồng nhất hệ số tìm \(a,\,\,b\) và tính tổng \(T = a + b\). Lời giải chi tiết: Ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\left( {\sqrt x + \sqrt {x + 1} } \right)f'\left( x \right) = 1\,\,\,\,\forall x \ge - 1\\ \Leftrightarrow f'\left( x \right) = \dfrac{1}{{\sqrt x + \sqrt {x + 1} }}\,\,\,\,\forall x \ge - 1\\ \Leftrightarrow f'\left( x \right) = \sqrt {x + 1} - \sqrt x \,\,\,\,\forall x \ge - 1\end{array}\) \( \Rightarrow f\left( x \right) = \int {\left( {\sqrt {x + 1} - \sqrt x } \right)dx} = \dfrac{2}{3}\left( {\left( {x + 1} \right)\sqrt {x + 1} - x\sqrt x } \right) + C\) Mà \(f\left( 0 \right) = \dfrac{2}{3}\)\( \Rightarrow \dfrac{2}{3}\left( {1 - 0} \right) + C = \dfrac{2}{3} \Rightarrow C = 0\). \( \Rightarrow f\left( x \right) = \dfrac{2}{3}\left( {\left( {x + 1} \right)\sqrt {x + 1} - x\sqrt x } \right)\). Khi đó ta có: \(\begin{array}{l}\int\limits_0^1 {f\left( x \right)dx} = \dfrac{2}{3}\int\limits_0^1 {\left( {\left( {x + 1} \right)\sqrt {x + 1} - x\sqrt x } \right)dx} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{2}{3}.\dfrac{2}{5}\left. {\left( {{{\left( {x + 1} \right)}^2}\sqrt {x + 1} - {x^2}\sqrt x } \right)} \right|_0^1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{4}{{15}}\left[ {\left( {4\sqrt 2 - 1} \right) - \left( {1 - 0} \right)} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{16\sqrt 2 - 8}}{{15}}\\ \Rightarrow \left\{ \begin{array}{l}a = 16\\b = - 8\end{array} \right.\end{array}\) Vậy \(T = a + b = 16 + \left( { - 8} \right) = 8.\) Chọn D. Câu hỏi 40 : Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_0^1 {f\left( x \right)dx} = 2;\,\,\,\int\limits_0^3 {f\left( x \right)dx = 6.} \) Giá trị của \(\int\limits_{ - 1}^1 {f\left( {\left| {2x - 1} \right|} \right)} dx\) bằng:
Đáp án: B Phương pháp giải: Sử dụng tính chất của tích phân: \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} .\) Sử dụng phương pháp tích phân đổi biến. Lời giải chi tiết: Ta có: \(\int\limits_{ - 1}^1 {f\left( {\left| {2x - 1} \right|} \right)} dx = \int\limits_{ - 1}^{\dfrac{1}{2}} {f\left( { - 2x - 1} \right)dx} + \int\limits_{\dfrac{1}{2}}^1 {f\left( {2x - 1} \right)dx} \) Đặt \({I_1} = \int\limits_{ - 1}^{\dfrac{1}{2}} {f\left( { - 2x - 1} \right)dx} ;\,\,\,\,{I_2} = \int\limits_{\dfrac{1}{2}}^2 {f\left( {2x - 1} \right)dx} \) Tính \({I_1} = \int\limits_{ - 1}^{\dfrac{1}{2}} {f\left( { - 2x - 1} \right)dx} \) Đặt \( - 2x - 1 = t \Rightarrow dt = - 2dx \Rightarrow dx = - \dfrac{1}{2}dt\) Đổi cận: \(\left\{ \begin{array}{l}x = - 1 \Rightarrow t = 3\\x = \dfrac{1}{2} \Rightarrow t = 0\end{array} \right..\) \( \Rightarrow {I_1} = - \dfrac{1}{2}\int\limits_3^0 {f\left( t \right)dt} = \dfrac{1}{2}\int\limits_0^3 {f\left( t \right)dt} = \dfrac{1}{2}\int\limits_0^3 {f\left( x \right)dx} = \dfrac{1}{2}.6 = 3.\) Tính \({I_2} = \int\limits_{\dfrac{1}{2}}^1 {f\left( {2x + 1} \right)dx} \) Đặt \(2x - 1 = t \Rightarrow dt = 2dx \Rightarrow dx = \dfrac{1}{2}dt\) Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 1\\x = \dfrac{1}{2} \Rightarrow t = 0\end{array} \right..\) \(\begin{array}{l} \Rightarrow {I_2} = \dfrac{1}{2}\int\limits_0^1 {f\left( t \right)dt} = \dfrac{1}{2}\int\limits_0^1 {f\left( x \right)dx} = \dfrac{1}{2}.2 = 1.\\ \Rightarrow I = {I_1} + {I_2} = 3 + 1 = 4.\end{array}\) Chọn B.
|