Phương pháp giải:

Lời giải chi tiết:

\({S_{hv}} = 4 \Rightarrow \) cạnh hình vuông bằng 2.

\(V\left( {I; - 2} \right) \Rightarrow \) cạnh hình vuông mới bằng \(\left| { - 2} \right|\).cạnh hình vuông cũ.

\( \Rightarrow \) Cạnh hình vuông mới bằng \(4\)

\( \Rightarrow {S_m} = {4^2} = 16\)

\( \Rightarrow \dfrac{{{S_c}}}{{{S_m}}} = \dfrac{4}{{16}} = \dfrac{1}{4} \Rightarrow \)\(S\)tăng 4 lần

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\(\begin{array}{l}{V_{\left( {I;3} \right)}}\left( {AB} \right) = A'B' \Rightarrow A'B' = 3AB\\{V_{\left( {I;3} \right)}}\left( {AC} \right) = A'C' \Rightarrow A'C' = 3AC\\{V_{\left( {I;3} \right)}}\left( {BC} \right) = B'C' \Rightarrow B'C' = 3BC\\ \Rightarrow \dfrac{{{P_{A'B'C'}}}}{{{P_{ABC}}}} = \dfrac{{3\left( {AB + AC + BC} \right)}}{{AB + AC + BC}} = 3\end{array}\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

Vô số tâm vì tự tùy ý với tỷ số vị tự \(k = 1\).

Chọn D.

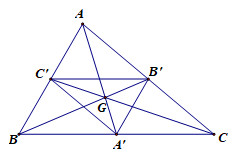
Phương pháp giải:

Lời giải chi tiết:

Có vô số tỉ số vị tự.

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

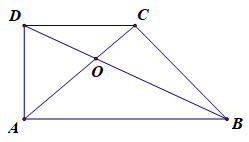
\(\begin{array}{l}V\left( {G;k} \right)A = A'\\ \Rightarrow \overrightarrow {GA} = k\overrightarrow {GA'} \Rightarrow k = - 2\end{array}\)

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

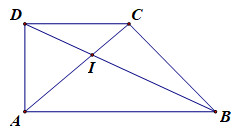
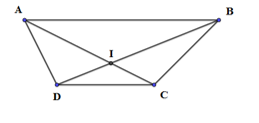
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)

\(\begin{array}{l}{V_{\left( {O;k} \right)}}\left( A \right) = C,\,\,\,{V_{\left( {O;k} \right)}}\left( B \right) = D\\ \Rightarrow \overrightarrow {CD}  = k\overrightarrow {AB}  \Rightarrow k = \dfrac{1}{3}\end{array}\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

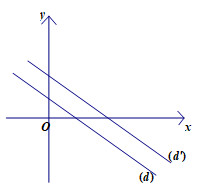
\(\begin{array}{l}AC \cap BD = \left\{ I \right\}\\{V_{\left( {I;k} \right)}}\left( {AB} \right) = CD\\k\overrightarrow {AB}  = \overrightarrow {CD}  \Rightarrow k =  - \dfrac{1}{2}\end{array}\)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Có vô số phép vị tự biến \(\left( d \right)\) thành chính nó.

Có vố phép vị tự biến \(\left( {d'} \right)\) thành chính nó.

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Cho điểm \(I\) cố định và một số \(k \ne 0\) phép vị tự tâm \(I\) có tỉ số \(k\) là phép biến \(M \in \left( d \right)\) thành \(M' \in \left( {d'} \right)\) sao cho \(\overrightarrow {IM'}  = k\overrightarrow {IM} \)

\( \Rightarrow \) Có vô số phép vị tự (vì có thể có nhiều tâm vị tự).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Vì đây là phép vị tự tâm \(O\)(điểm duy nhất)

\( \Rightarrow \) Chỉ có 1 phép vị tự tâm \(O\) biến \(\left( d \right)\) thành \(\left( {d'} \right)\)

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

\(\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 5\) có tâm \(A\left( {3; - 1} \right)\), bán kính \(R = \sqrt 5 \)

Phép vị tự tỉ số \(k =  - 2 \Rightarrow {R_{\left( {C'} \right)}} = \left| { - 2} \right|.\sqrt 5  = 2\sqrt 5 \)

\(\overrightarrow {IA'}  = \left( { - 2} \right).\overrightarrow {IA} \)

Gọi \(A'\left( {x;y} \right)\)\( \Rightarrow \overrightarrow {IA'} \left( {x - 1;y - 2} \right);\,\,\,\overrightarrow {IA} \left( {2; - 3} \right)\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}x - 1 = \left( { - 2} \right).2\\y - 2 = \left( { - 2} \right).\left( { - 3} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 3\\y = 8\end{array} \right.\\ \Rightarrow \left( {C'} \right):{\left[ {x - \left( { - 3} \right)} \right]^2} + {\left( {y - 8} \right)^2} = {\left( {2\sqrt 5 } \right)^2}\\ \Leftrightarrow {\left( {x + 3} \right)^2} + {\left( {y - 8} \right)^2} = 20\end{array}\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\(\begin{array}{l}d:x - 2y + 6 = 0\\d':x - 2y - 6 = 0\\{V_{\left( {I;k} \right)}}\left( d \right) = d'\end{array}\)

Lấy điểm \(A\left( {0;3} \right) \in d\)

\(\begin{array}{l} \Rightarrow {V_{\left( {I;k} \right)}}\left( A \right) = A'\left( {x;y} \right) \in d'\\ \Leftrightarrow \overrightarrow {IA'}  = k\overrightarrow {IA} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 2 = k\left( {0 - 2} \right)\\y - 2 = k\left( {3 - 2} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 2k + 2\\y = k + 2\end{array} \right.\end{array}\)

Thay tọa độ điểm \(A'\) vào phương trình \(d'\), ta có: \(\left( { - 2k + 2} \right) - 2\left( {k + 2} \right) - 6 = 0\)\( \Leftrightarrow k =  - 2\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\({V_{\left( {I;2} \right)}}\left( d \right) = \Delta  \Rightarrow d\parallel \Delta \)\( \Rightarrow \) Phương trình \(\Delta \) có dạng \(x - y + c = 0.\)

Lấy điểm \(A\left( {0;2} \right) \in d\)

\(\begin{array}{l} \Rightarrow A'\left( {x;y} \right) \in \Delta ,\,\,A' = {V_{\left( {I;2} \right)}}\left( A \right) \Rightarrow \overrightarrow {IA'}  = 2\overrightarrow {IA} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 0 = 2\left( {0 - 0} \right)\\y - 5 = 2\left( {2 - 5} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y =  - 1\end{array} \right. \Rightarrow A'\left( {0; - 1} \right)\end{array}\)

Thay tọa độ điểm \(A'\) vào phương trình \(\Delta \) ta có: \(0 - \left( { - 1} \right) + c = 0 \Leftrightarrow c =  - 1\)

\( \Rightarrow \) Phương trình \(\Delta :x - y - 1 = 0\)

\( \Rightarrow d\left( {0;\Delta } \right) = \dfrac{{\left| {0 - 0 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{1}{{\sqrt 2 }}.\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\(\begin{array}{l}d:2x + y - 4 = 0\\{V_{\left( {I; - 2} \right)}}\left( d \right) = \left( {d'} \right) \Rightarrow d\parallel d'\end{array}\)

\( \Rightarrow \) Phương trình \(d\) có dạng \(2x + y + c = 0\)

Lấy điểm \(A\left( {2;0} \right) \in d\)

\(\begin{array}{l} \Rightarrow A\left( {x;y} \right) \in d',\,\,A' = {V_{\left( {I; - 2} \right)}}\left( A \right) \Rightarrow \overrightarrow {IA'}  =  - 2\overrightarrow {IA} \\ \Leftrightarrow \left\{ \begin{array}{l}x + 1 =  - 2\left( {2 + 1} \right)\\y - 2 =  - 2\left( {0 - 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 7\\y = 6\end{array} \right.\\ \Rightarrow A'\left( { - 7;6} \right)\end{array}\)

Thay tọa độ \(A'\left( { - 7;6} \right)\) vào \(d'\) ta có: \(2.\left( { - 7} \right) + 6 + c = 0 \Leftrightarrow c = 8.\)

\( \Rightarrow \) Phương trình đường thẳng \(d':2x + y + 8 = 0\).

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\(\Delta :2x + 3y = 5 \Leftrightarrow 2x + 3y - 5 = 0\)

\({V_{\left( {I;3} \right)}}\left( \Delta  \right) = d \Leftrightarrow \Delta \parallel d \Rightarrow \) Phương trình đường thẳng \(d\) có dạng: \(2x + 3y + c = 0\)

Lấy điểm \(A\left( {1;1} \right) \in \Delta \)

\(\begin{array}{l} \Rightarrow A'\left( {x;y} \right) \in d,\,\,A' = {V_{\left( {I;3} \right)}}\left( A \right) \Rightarrow \overrightarrow {IA'}  = 3\overrightarrow {IA} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 3\left( {1 - 1} \right)\\y - 5 = 3\left( {1 - 5} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 7\end{array} \right.\\ \Rightarrow A'\left( {1; - 7} \right)\end{array}\)

Thay tọa độ điểm \(A'\) vào phương trình \(d\) ta có: \(2.1 + 3.\left( { - 7} \right) + c = 0 \Leftrightarrow c = 19\)

\( \Rightarrow \) Phương trình \(d\) là \(2x + 3y + 19 = 0\)

Thay lần lượt 4 đáp án vào ta thấy chỉ có điểm \(\left( { - 8; - 1} \right)\) thỏa mãn và thuộc đường thẳng \(d\).

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\(\left( {{C_1}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 1\) \( \Rightarrow \) tâm \({I_1}\left( {3; - 1} \right)\), bán kinh \({R_1} = 1\)

\(\left( {{C_2}} \right):{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 4\)\( \Rightarrow \) tâm \({I_2}\left( {4;3} \right)\), bán kinh \({R_2} = 2\)

Gọi \(I\) là tâm vị tự của 2 đường tròn với \(I\left( {x;y} \right)\)

Ta có: \(\left\{ \begin{array}{l}\overrightarrow {I\,{I_1}} \left( {1 - x;3 - y} \right)\\\overrightarrow {I\,{I_2}} \left( {4 - x;3 - y} \right)\end{array} \right.\)

\(k = \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{1}{2}\) (\(k > 0\) vì đây là vị tự ngoài)

\(\begin{array}{l} \Rightarrow \overrightarrow {I\,{I_1}}  = \dfrac{1}{2}\overrightarrow {I\,{I_2}} \\ \Leftrightarrow \left\{ \begin{array}{l}1 - x = \dfrac{1}{2}\left( {4 - x} \right)\\3 - y = \dfrac{1}{2}\left( {3 - y} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 2\\y = 3\end{array} \right.\end{array}\)

Vậy vị tự tâm ngoài \(\left( { - 2;3} \right)\).

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

\({V_{\left( {I; - 4} \right)}}\,\left( \Delta  \right) = d \Rightarrow \Delta \parallel d\)\( \Rightarrow \) Phương trình \(d\) có dạng: \(x - 2y + c = 0\)

Lấy điểm \(A\left( {0;3} \right) \in \Delta \)

\(\begin{array}{l} \Rightarrow A'\left( {x;y} \right) \in d,\,\,\,A' = {V_{\left( {I; - 4} \right)}}\left( A \right)\\ \Leftrightarrow \overrightarrow {IA'}  =  - 4\overrightarrow {IA} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 2 =  - 4\left( {0 - 2} \right)\\y - m =  - 4\left( {3 - m} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 10\\y = 5m - 12\end{array} \right.\end{array}\)

Thay tọa độ điểm \(A'\) vào phương trình \(d'\) ta có: \(10 - 2\left( {5m - 12} \right) + c = 0\,\left( 1 \right)\)

Ta có

\(\begin{array}{l}H\left( {16;1} \right) \in d \Rightarrow 16 - 2.1 + c = 0 \Leftrightarrow c =  - 14\\ \Rightarrow \left( 1 \right) \Leftrightarrow 10 - 2\left( {5m - 12} \right) - 14 = 0 \Leftrightarrow m = 2\end{array}\)

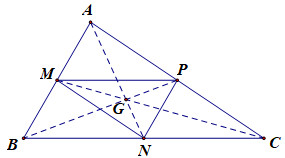
Chọn D.

Phương pháp giải:

Lời giải chi tiết:

\(\left\{ \begin{array}{l}{V_{\left( {O; - 1} \right)}}\\A\left( {3;2} \right)\end{array} \right.\)

Qua \({V_{\left( {O; - 1} \right)}}\) biến \(A\) thành \(A'\)

\(\begin{array}{l} \Rightarrow \overrightarrow {OA'}  = k\overrightarrow {OA}  \Leftrightarrow \left( {x;y} \right) =  - 1\left( {3;2} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 3\\y =  - 2\end{array} \right. \Rightarrow A\left( { - 3; - 2} \right)\end{array}\)

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Qua \({V_{\left( {G;k} \right)}}\) biến \(A\) thành \(N\)

\(\begin{array}{*{20}{l}}
{ \Rightarrow \overrightarrow {GN} = k\overrightarrow {GA} }\\
{ \Rightarrow k = - \frac{1}{2}}
\end{array}\)

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Qua \({V_{\left( {I;3} \right)}}\) biến \(A\left( {4;4} \right)\) thành \(B\left( {8;8} \right)\)            

\(\begin{array}{l} \Rightarrow \overrightarrow {IB}  = k\overrightarrow {IA} \\ \Leftrightarrow \left( {8 - a;8 - b} \right) = 3\left( {4 - a;4 - b} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}8 - a = 12 - 3a\\8 - b = 12 - 3b\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 2\end{array} \right. \Rightarrow a + b = 4\end{array}\)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

\(M\left( {x;y} \right)\) là điểm bất kì thuộc \(d\)

\(M'\left( {x';y'} \right)\) là ảnh của \(M\) qua \(V\left( {I;2} \right)\)

\(\begin{array}{l}{V_{\left( {I;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {IM'}  = k\overrightarrow {IM} \\ \Leftrightarrow \left( {x' - 1;y' - 2} \right) = 2\left( {x - 1;y - 2} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x' - 1 = 2x - 2\\y' - 2 = 2y - 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{x' + 1}}{2}\\y = \dfrac{{y' + 2}}{2}\end{array} \right.\end{array}\)

Thay \(\left( {x;y} \right)\) vào \(d\):

\(\begin{array}{l}\dfrac{{y' + 2}}{2} = \dfrac{{x' + 1}}{2} + 1\\ \Leftrightarrow y' + 2 = x' + 1 + 2\\ \Leftrightarrow y' = x' + 1\\ \Leftrightarrow y' - x' - 1 = 0\\ \Leftrightarrow x' - y' + 1 = 0\end{array}\)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Qua \({V_{\left( {I;2} \right)}}\) biến \(A\left( {1; - 2} \right)\) thành \(A'\left( { - 5;1} \right)\)

\(\begin{array}{l} \Rightarrow \overrightarrow {IA'}  = 2\overrightarrow {IA} \\ \Leftrightarrow \left( { - 5 - x;1 - y} \right) = 2\left( {1 - x; - 2 - y} \right)\\ \Leftrightarrow \left\{ \begin{array}{l} - 5 - x = 2 - 2x\\1 - y =  - 4 - 2y\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 7\\y =  - 5\end{array} \right. \Rightarrow I\left( {7; - 5} \right)\end{array}\)

Qua \(V\left( {I;2} \right)\) biến \(B\left( {0;1} \right)\) thành \(B'\):

\(\begin{array}{l} \Rightarrow \overrightarrow {IB'}  = 2\overrightarrow {IB} \\ \Leftrightarrow \left( {x - 7;y + 5} \right) = 2\left( { - 7;6} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 7\\y = 7\end{array} \right. \Rightarrow B\left( { - 7;7} \right)\end{array}\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 5\) có tâm \(I\left( {1; - 2} \right)\), bán kính \(R = \sqrt 5 \)

Ta có: Phép vị tự tâm \(O\) tỉ số \(k =  - 2\)

\( \Rightarrow {R_{\left( {C'} \right)}} = \left| k \right|.{R_{\left( C \right)}}\)\( \Leftrightarrow {R_{\left( {C'} \right)}} = \left| { - 2} \right|.\sqrt 5  = 2\sqrt 5 \)

Phép vị tự tâm \(O\) tỉ số \(k =  - 2\) biến \(I\left( {1; - 2} \right)\) thành \(I'\left( {x;y} \right)\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}x = 1.\left( { - 2} \right)\\y = \left( { - 2} \right).\left( { - 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 2\\y = 4\end{array} \right.\\ \Rightarrow I'\left( { - 2;4} \right)\\ \Rightarrow \left( {C'} \right):{\left[ {x - \left( { - 2} \right)} \right]^2} + {\left( {y - 4} \right)^2} = {\left( {2\sqrt 5 } \right)^2}\\\,\,\,\,\,\,\,\,\,\, \Leftrightarrow {\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} = 20\end{array}\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\(\left\{ \begin{array}{l}{V_{\left( {I; - 2} \right)}}\\I\left( {1;3} \right)\\A'\left( {1;2} \right)\end{array} \right.\)

Qua \({V_{\left( {I; - 2} \right)}}\) biến \(A\) thành \(A'\)

\(\begin{array}{l} \Rightarrow \overrightarrow {IA'}  = k\overrightarrow {IA}  \Leftrightarrow \left( {0; - 1} \right) =  - 2\left( {x - 1;y - 3} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = \dfrac{7}{2}\end{array} \right. \Rightarrow A\left( {1;\dfrac{7}{2}} \right).\end{array}\)

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

\(\left\{ \begin{array}{l}{V_{\left( {I; - 2} \right)}}\\I\left( {3; - 1} \right)\\M\left( {4;5} \right)\end{array} \right.\)

Qua\({V_{\left( {I; - 2} \right)}}\) biến \(M\) thành \(M'\)

\(\begin{array}{l} \Rightarrow \overrightarrow {IM'}  = k\overrightarrow {IM}  \Leftrightarrow \left( {x - 3;y + 1} \right) =  - 2\left( {1;6} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 13\end{array} \right. \Rightarrow M'\left( {1; - 13} \right).\end{array}\)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Với 2 đường tròn bất kì chỉ có 1 phép vị tự biến đường tròn này thành đường tròn kia.

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

\(\overrightarrow {IM'}  = k\overrightarrow {IM} \)

Tỉ số \(k\) biến \(M\) thành chính nó

\( \Rightarrow k = 1\)

Chọn B.

Phương pháp giải:

Áp dụng tính chất của phép vị tự.

Lời giải chi tiết:

\(\begin{array}{l}\left\{ \begin{array}{l}{V_{\left( {I; - 2} \right)}}\left( M \right) = M'\\{V_{\left( {I; - 2} \right)}}\left( N \right) = N'\end{array} \right. \Rightarrow M'N' = 2MN\\M\left( {3; - 4} \right);N\left( {0; - 2} \right) \Rightarrow MN = \sqrt {13} \\ \Rightarrow M'N' = 2\sqrt {13} \end{array}\)

Chọn B.

Phương pháp giải:

Từ biểu thức đã có tìm tọa độ điểm A, rồi tìm ảnh của điểm qua qua định nghĩa phép vị tự.

Lời giải chi tiết:

Ta có \(\overrightarrow {OA}  = \overrightarrow i  - 7\overrightarrow j  \Rightarrow \left\{ \begin{array}{l}{x_A} = 1\\{y_A} =  - 7\end{array} \right.\).

Nên \({V_{\left( {O; - 3} \right)}}\left( A \right) = A' \Leftrightarrow \overrightarrow {OA'}  =  - 3\overrightarrow {OA}  \Rightarrow A'\left( { - 3;21} \right)\).

Chọn D.

Phương pháp giải:

Tìm ảnh của tâm I đường tròn, bán kính tăng 2 lần.

Lời giải chi tiết:

Ta có: Tâm \(A\left( {1; - 3} \right),\,\,R = 3\) của \(\left( C \right)\). Khi đó bán kính mới là: \(R' = 3 \times 2 = 6\)

Lại có: \({V_{\left( {I;2} \right)}}\left( A \right) = A' \Leftrightarrow \overrightarrow {IA'}  = 2.\overrightarrow {IA}  \Rightarrow \left\{ \begin{array}{l}{x_{A'}} - 3 = 2.\left( {1 - 3} \right)\\{y_{A'}} - 2 = 2.\left( { - 3 - 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} =  - 1\\{y_{A'}} =  - 8\end{array} \right.\) nên \(A'\left( { - 1; - 8} \right)\).

Vậy ảnh của đường tròn \(\left( C \right)\) là \({\left( {x + 1} \right)^2} + {\left( {y + 8} \right)^2} = 36\).

Chọn A.

Phương pháp giải:

\({V_{\left( {A;\dfrac{3}{2}} \right)}}\left( {\Delta ABC} \right) = \Delta AB'C'\) \( \Rightarrow \) Bán kính \(R\) của đường tròn ngoại tiếp \(\Delta AB'C'\) gấp \(\dfrac{3}{2}\) lần bán kính của đường tròn ngoại tiếp \(\Delta ABC\).

Lời giải chi tiết:

\(\left\{ \begin{array}{l}{V_{\left( {A;\dfrac{3}{2}} \right)}}\left( A \right) = A\\{V_{\left( {A;\dfrac{3}{2}} \right)}}\left( B \right) = B'\\{V_{\left( {A;\dfrac{3}{2}} \right)}}\left( C \right) = C'\end{array} \right. \Rightarrow {V_{\left( {A;\dfrac{3}{2}} \right)}}\left( {\Delta ABC} \right) = \Delta AB'C'\).

\( \Rightarrow \) Bán kính \(R\) của đường tròn ngoại tiếp \(\Delta AB'C'\) gấp \(\dfrac{3}{2}\) lần bán kính của đường tròn ngoại tiếp \(\Delta ABC\).

Tam giác \(ABC\) vuông tại \(A\) nên đường tròn ngoại tiếp \(\Delta ABC\) là

\(r = \dfrac{1}{2}BC = \dfrac{1}{2}\sqrt {A{B^2} + A{C^2}}  = \dfrac{1}{2}\sqrt {{6^2} + {8^2}}  = 5\).

Vậy \(R = \dfrac{3}{2}r = \dfrac{3}{2}.5 = \dfrac{{15}}{2}\).

Chọn C.

Phương pháp giải:

\({V_{\left( {I;k} \right)}}\left( {\Delta ABC} \right) = \Delta A'B'C' \Rightarrow {S_{\Delta A'B'C'}} = {k^2}.{S_{\Delta ABC}}\).

Lời giải chi tiết:

\({V_{\left( {I;3} \right)}}\left( {\Delta ABC} \right) = \Delta A'B'C' \Rightarrow {S_{\Delta A'B'C'}} = 9.{S_{\Delta ABC}}\).

Chọn D.

Phương pháp giải:

Phép vị tự tâm \(I\), tỉ số \(k\) biến đường tròn bán kính \(R\) thành đường tròn có bán kính \(R' = \left| k \right|R\).

Lời giải chi tiết:

Đường tròn \(\left( C \right):\,\,{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 25\) có bán kính \(R = 5\).

Phép vị tự tỉ số \(k =  - \dfrac{1}{2}\) biến đường tròn \(\left( C \right)\) thành đường tròn có bán kính \(R' = \left| { - \dfrac{1}{2}} \right|R = \dfrac{1}{2}.5 = \dfrac{5}{2}\).

Chọn B.

Phương pháp giải:

- Xác định tâm \(J\) và bán kính \(R\) của đường tròn \(\left( C \right)\).

- Tìm \(J' = {V_{\left( {I;k} \right)}}\left( J \right)\), bán kính \(R' = \left| k \right|R\).

- Viết phương trình đường tròn \(\left( {C'} \right)\) tâm \(J'\) bán kính \(R'\).

Lời giải chi tiết:

Đường tròn \(\left( C \right)\) có tâm \(J\left( {1; - 2} \right)\) bán kính \(R = \sqrt {{1^2} + {{\left( { - 2} \right)}^2} - \left( { - 4} \right)}  = \sqrt 9  = 3\).

Gọi \(J'\left( {x;y} \right)\) là ảnh của \(J\) của phép vị tự tâm \(I\) tỉ số \(k = 2\) ta có:

\({V_{\left( {I;2} \right)}}\left( J \right) = J' \Leftrightarrow \overrightarrow {IJ'}  = 2\overrightarrow {IJ}  \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 2\left( {1 - 2} \right)\\y - 1 = 2\left( { - 2 - 1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y =  - 5\end{array} \right. \Rightarrow J'\left( {0; - 5} \right)\).

Gọi \(\left( {C'} \right) = {V_{\left( {I;2} \right)}}\left( C \right) \Rightarrow \left( {C'} \right)\) là đường tròn tâm \(J'\left( {0;5} \right)\) bán kính \(R' = 2R = 6\).

Vậy phương trình \(\left( {C'} \right):\,\,{x^2} + {\left( {y + 5} \right)^2} = 36\).

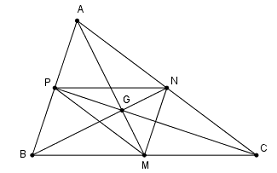
Phương pháp giải:

Phép vị tự tâm O tỉ số \(k\) biến \(M\left( {x;y} \right) \mapsto M'\left( {x';y'} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}x' = kx\\y' = ky\end{array} \right.\)

Phép quay tâm O góc quay  \(180^\circ \) biến \(M\left( {x;y} \right) \mapsto M'\left( {x';y'} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}x' =  - x\\y' =  - y\end{array} \right.\)

Lời giải chi tiết:

Lấy \(M\left( {x;y} \right) \in \left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\)

Phép vị tự tâm O tỉ số \(k = \dfrac{1}{2}\) biến \(M\left( {x;y} \right) \mapsto M'\left( {x';y'} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}x' = \dfrac{1}{2}x\\y' = \dfrac{1}{2}y\end{array} \right.\)

Phép quay tâm O góc quay  \(180^\circ \) biến \(M'\left( {x';y'} \right) \mapsto M''\left( {x'';y''} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}x'' =  - x'\\y'' =  - y'\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}x'' =  - \dfrac{1}{2}x\\y'' =  - \dfrac{1}{2}y\end{array} \right.\,\, \Leftrightarrow \left\{ \begin{array}{l}x =  - 2x''\\y =  - 2y''\end{array} \right.\)

\( \Rightarrow {\left( {2x'' - 2} \right)^2} + {\left( {2y'' - 2} \right)^2} = 4 \Leftrightarrow {\left( {x'' - 1} \right)^2} + {\left( {y'' - 1} \right)^2} = 1\)

Vậy phương trình của đường tròn cần tìm là \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\).

Chọn: A

Phương pháp giải:

Phép vị tự tâm \(A\) tỉ số \(k\): \({V_{\left( {I;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {IM'}  = k\overrightarrow {IM} \)

Lời giải chi tiết:

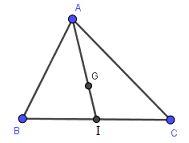
Vì \(G\) là trọng tâm tam giác \(ABC\) nên \(\dfrac{{GM}}{{GA}} = \dfrac{{GN}}{{GB}} = \dfrac{{GP}}{{GC}} = \dfrac{1}{2}\)  hay \(\overrightarrow {GM}  =  - \dfrac{1}{2}\overrightarrow {GA} ;\,\overrightarrow {GN}  =  - \dfrac{1}{2}\overrightarrow {GB} ;\,\overrightarrow {GP}  =  - \dfrac{1}{2}\overrightarrow {GC} \)

Xét phép vị tự tâm \(G\) tỉ số \( - \dfrac{1}{2}\)  ta có \({V_{\left( {G; - \dfrac{1}{2}} \right)}}\left( A \right) = M\), \({V_{\left( {G; - \dfrac{1}{2}} \right)}}\left( B \right) = N\), \({V_{\left( {G; - \dfrac{1}{2}} \right)}}\left( C \right) = P\) (do \(\overrightarrow {GM}  =  - \dfrac{1}{2}\overrightarrow {GA} ;\,\overrightarrow {GN}  =  - \dfrac{1}{2}\overrightarrow {GB} ;\,\overrightarrow {GP}  =  - \dfrac{1}{2}\overrightarrow {GC} \) (cmt))

Hay phép vị tự tâm \(G\) tỉ số \( - \dfrac{1}{2}\)  biến tam giác \(ABC\) thành tam giác \(MNP\).

Chọn D

Phương pháp giải:

Phép vị tự tâm \(I\) tỉ số \(k\) biến \(M\) thành \(M'\) thì \(\overrightarrow {IM'}  = k\overrightarrow {IM} \)

Lời giải chi tiết:

Gọi \(I\) là trung điểm của \(BC\).

Vì \(G\) là trọng tâm tam giác \(ABC\), ta có \(IG = \dfrac{1}{3}IA\)  suy ra \(\overrightarrow {IG}  = \dfrac{1}{3}\overrightarrow {IA} \)  nên phép vị tự tâm \(I\) tỉ số \(\dfrac{1}{3}\) biến \(A\) thành \(G.\)

Mà điểm \(A\) chạy trên đường tròn \(\left( {O;R} \right)\) cố định nên quỹ tích điểm \(G\) là ảnh của đường tròn \(\left( {O;R} \right)\) qua phép vị tự tâm \(I\) tỉ số \(\dfrac{1}{3}\).

Chọn C

Phương pháp giải:

\({V_{\left( {I;k} \right)}}\left( A \right) = A' \Leftrightarrow \overrightarrow {IA'}  = k\overrightarrow {IA} \).

Lời giải chi tiết:

\({V_{\left( {I;2} \right)}}\left( A \right) = A'\left( {x;y} \right) \Leftrightarrow \overrightarrow {IA'}  = 2\overrightarrow {IA}  \Leftrightarrow \left\{ \begin{array}{l}x - 3 = 2\left( {1 - 3} \right)\\y - 4 = 2\left( {2 - 4} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = 0\end{array} \right. \Rightarrow A'\left( { - 1;0} \right)\).

Chọn A.

Phương pháp giải:

\({V_{\left( {I;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {IM'}  = k\overrightarrow {IM} \)

Lời giải chi tiết:

\(\overrightarrow {DC}  = \dfrac{1}{2}\overrightarrow {AB}  \Rightarrow \left\{ \begin{array}{l}\overrightarrow {IC}  =  - \dfrac{1}{2}\overrightarrow {IA} \\\overrightarrow {ID}  =  - \dfrac{1}{2}\overrightarrow {IB} \end{array} \right.\,\, \Rightarrow {V_{\left( {I;k =  - \dfrac{1}{2}} \right)}}:AB \mapsto CD\)

Chọn: A

Phương pháp giải:

\({V_{\left( {I;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {IM'}  = k\overrightarrow {IM} \).

Lời giải chi tiết:

Gọi \(M'\left( {x;y} \right) = {V_{\left( {O; - 2} \right)}}\left( M \right) \Rightarrow \overrightarrow {OM'}  =  - 2\overrightarrow {OM}  \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y =  - 2\end{array} \right. \Rightarrow M'\left( {6; - 2} \right)\).

Chọn D.