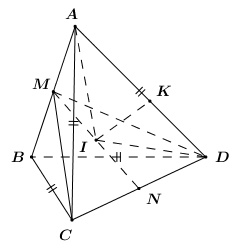
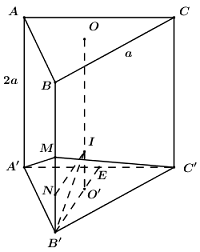
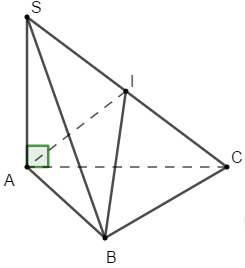
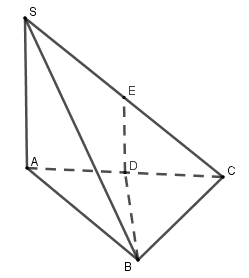
40 bài tập trắc nghiệm mặt cầu mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Cho tứ diện \(ABCD\) có \(AB = a;\)\(AC = BC = AD = BD = \dfrac{{a\sqrt 3 }}{2}\). Gọi \(M,\,\,N\) là trung điểm của \(AB,\,\,CD\). Góc giữa hai mặt phẳng \(\left( {ABD} \right);\,\,\left( {ABC} \right)\) là \(\alpha \) . Tính \({\rm{cos}}\alpha \) biết mặt cầu đường kính \(MN\) tiếp xúc với cạnh \(AD\).
Đáp án: B Phương pháp giải: - Xác định góc \(\alpha \): Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến. - Tính \(\cos \alpha \) bằng cách sử dụng định lý cô sin trong tam giác: \(\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\). Lời giải chi tiết:
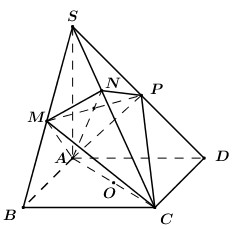
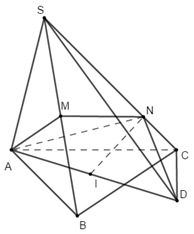
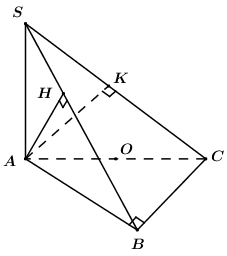
Xét các tam giác ACB, ADB lần lượt cân tại C và D nên \(CM \bot AB,DM \bot AB\) Ta có : \(\left\{ \begin{array}{l}\left( {ABC} \right) \cap \left( {ABD} \right) = AB\\CM \bot AB,CM \subset \left( {ABC} \right)\\DM \bot AB,DM \subset \left( {ABD} \right)\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABD} \right)} \right) = \angle \left( {CM;DM} \right)\). Tam giác ACM vuông tại M nên theo Pitago ta có : \(\begin{array}{l}C{M^2} = A{C^2} - A{M^2}\\ \Rightarrow CM = \sqrt {A{C^2} - A{M^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{2}\end{array}\) Tương tự \(DM = \dfrac{{a\sqrt 2 }}{2}\). Gọi K là hình chiếu của I lên AD ta có : Mặt cầu đường kính MN tiếp xúc với AD nên \(IK = IM = IN,IK \bot AD\). Xét tam giác AMI và AKI có : \(\begin{array}{l}\widehat {AMI} = \widehat {AKI} = {90^0};\\AI\,chung;\\IM = IK\left( {cmt} \right);\end{array}\) Do đó \(\Delta AMI = \Delta AKI\) (cạnh huyền – cạnh góc vuông) \( \Rightarrow AK = AM = \dfrac{a}{2}\) (cạnh tương ứng). Tương tự : \(\Delta DNI = \Delta DKI\) (cạnh huyền – cạnh góc vuông) \(\begin{array}{l} \Rightarrow DN = DK = AD - AK = \dfrac{{a\sqrt 3 }}{2} - \dfrac{a}{2} = \dfrac{{a\left( {\sqrt 3 - 1} \right)}}{2}\\ \Rightarrow DC = 2DN = 2.\dfrac{{a\left( {\sqrt 3 - 1} \right)}}{2} = a\left( {\sqrt 3 - 1} \right)\end{array}\) Ap dụng định lý cô sin trong tam giác MCD có : \(\begin{array}{l}\cos \widehat {CMD} = \dfrac{{M{C^2} + M{D^2} - C{D^2}}}{{2MC.MD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} - {{\left( {a\left( {\sqrt 3 - 1} \right)} \right)}^2}}}{{2.\dfrac{{a\sqrt 2 }}{2}.\dfrac{{a\sqrt 2 }}{2}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2\sqrt 3 - 3 > 0\\ \Rightarrow \cos \alpha = \cos \widehat {CMD} = 2\sqrt 3 - 3\end{array}\) Chọn B. Câu hỏi 2 : Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(2\sqrt 2 \). Cạnh bên \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3\). Mặt phẳng \(\left( \alpha \right)\) qua \(A\) và vuông góc với \(SC\) cắt cạnh \(SB,\,\,SC,\,\,SD\) lần lượt tại \(M,\,\,N,\,\,P\). Thể tích \(V\) của khối cầu ngoại tiếp tứ diện \(CMNP\).
Đáp án: A Phương pháp giải: - Chứng minh \(\angle AMC = \angle ANC = \angle APC = {90^0}\) và suy ra khối cầu ngoại tiếp tứ diện \(CMNP\). - Xác định bán kính \(R\) của khối cầu. - Tinh thể tích khối cầu bán kính \(R\): \(V = \dfrac{4}{3}\pi {R^3}\). Lời giải chi tiết:
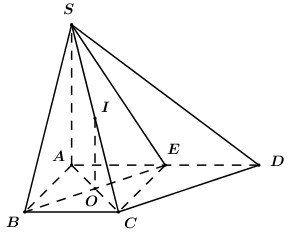
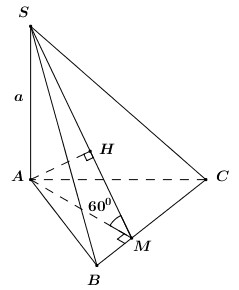
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM\). \(\left\{ \begin{array}{l}AM \bot BC\\AM \bot SC\end{array} \right. \Rightarrow AM \bot \left( {SBC} \right)\) \( \Rightarrow AM \bot MC\). \( \Rightarrow \angle AMC = {90^0}\) hay điểm \(M\) thuộc mặt cầu đường kính \(AC\). Chứng minh tương tự ta có \(AP \bot \left( {SCD} \right) \Rightarrow AP \bot PC \Rightarrow \angle APC = {90^0}\) hay \(P\) thuộc mặt cầu đường kính \(AC\). Lại có \(AN \bot SC \Rightarrow \angle ANC = {90^0}\) hay \(N\) thuộc mặt cầu đường kính \(AC\). Do đó \(CMNP\) nội tiếp khối cầu đường kính \(AC\) hay khối cầu ngoại tiếp tứ diện \(CMNP\) có bán kính \(R = \dfrac{1}{2}AC = \dfrac{1}{2}.2\sqrt 2 .\sqrt 2 = 2\). Vậy thể tích khối cầu cần tìm là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32\pi }}{3}\). Chọn A. Câu hỏi 3 : Cho hình chóp có \(SA \bot \left( {ABC} \right),\) \(AB = 3,\,\,AC = 2,\,\,\angle BAC = 60^\circ \). Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu ngoại tiếp chóp ABCNM.
Đáp án: B Phương pháp giải: Kẻ thêm đường kính của đường tròn ngoại tiếp tam giác ABC. Xét các mối quan hệ vuông góc rồi suy ra tâm mặt cầu cần tìm. Lời giải chi tiết: Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Kẻ đường kính AD của đường tròn tâm I. Khi đó \(\left\{ \begin{array}{l}C \in \left( {I;r} \right) \Rightarrow AC \bot CD\\SA \bot CD\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right)\) \(\begin{array}{l} \Rightarrow CD \bot AN;AN \bot SC\\ \Rightarrow AN \bot \left( {SCD} \right)\\ \Rightarrow AN \bot DN\end{array}\) \( \Rightarrow \angle AND = 90^\circ \) Nên N thuộc đường tròn \(\left( {I;r} \right)\) Tương tự ta có M thuộc đường tròn \(\left( {I;r} \right)\) Vậy mặt cầu ngoại tiếp ABCNM là mặt cầu \(\left( {I;r} \right)\) \( \Rightarrow r = IA\). Ta có \(2r = \frac{{BC}}{{\sin BAC}} = \frac{{\sqrt 7 }}{{\sin 60^\circ }} \Rightarrow r = \frac{{\sqrt {21} }}{3}\). Chọn B. Câu hỏi 4 : Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại \(A\) và \(B\). Biết \(SA\) vuông góc với \(\left( {ABCD} \right)\), \(AB = BC = a\), \(AD = 2a\), \(SA = a\sqrt 2 \). Gọi \(E\) là trung điểm của \(AD\). Bán kính mặt cầu đi qua các điểm \(S,\,\,A,\,\,B,\,\,C,\,\,E\) bằng:
Đáp án: D Phương pháp giải: - Gọi \(I\) là trung điểm của \(SC\), chứng minh \(IS = IA = IB = IC = IE\). - Sử dụng định lí Pytago để tính bán kính khối cầu. Lời giải chi tiết:
Xét tứ giác \(ABCE\) có \(AB = BC = AE = a,\,\,BC\parallel AE,\,\,\angle ABC = {90^0}\) nên \(ABCE\) là hình vuông. Gọi \(O = AC \cap BD\), \(I\) là trung điểm của \(SC\) ta có \(OI\parallel SA\) (\(OI\) là đường trung bình của tam giác \(SAC\)) nên \(OI \bot \left( {ABCD} \right)\). Do đó \(IA = IB = IC = IE\). Lại có \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A\) (tam giác vuông có trung điểm của cạnh huyền là tâm đường tròn ngoại tiếp tam giác). \( \Rightarrow IS = IA = IB = IC = IE\) \( \Rightarrow I\) là tâm mặt cầu đi qua các điểm \(S,\,\,A,\,\,B,\,\,C,\,\,E\), bán kính của khối cầu này là \(R = IS = \dfrac{1}{2}SC\). Vì là hình vuông cạnh nên \(AC = a\sqrt 2 \). Áp dụng định lí Pytago trong tam giác vuông có: \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {2{a^2} + 2{a^2}} = 2a\). Vậy \(R = \dfrac{1}{2}SC = a\). Chọn D. Câu hỏi 5 : Cho hình chóp đều \(S.ABC\) có chiều cao bằng \(h\) và cạnh bên bằng \(b\). Bán kính mặt cầu ngoại tiếp hình chóp bằng
Đáp án: C Phương pháp giải: - Xác định bán kính mặt cầu ngoại tiếp chóp là giao điểm của hai trục của hai mặt bất kì. - Sử dụng tam giác đồng dạng để tính bán kính mặt cầu. Lời giải chi tiết:
Gọi \(E\) là tâm tam giác đều \(ABC\) \( \Rightarrow SE \bot \left( {ABC} \right)\) và \(SE\) là trục của \(\left( {ABC} \right)\). Gọi \(F\) là trung điểm của \(SA\). Trong \(\left( {SAE} \right)\), từ \(F\) kẻ đường thẳng vuông góc với \(SA\) và cắt \(SE\) tại \(G\). Ta có: \(\left\{ \begin{array}{l}G \in SE \Rightarrow GA = GB = GC\\G \in GF \Rightarrow GS = GA\end{array} \right.\) \( \Rightarrow GA = GB = GC = GS\), do đó \(G\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\). Xét \(\Delta SFG\) và \(\Delta SEA\) có: \(\angle ASE\) chung, \(\angle SFG = \angle SEA = {90^0}\). \( \Rightarrow \Delta SFG \sim \Delta SEA\,\,\left( {g.g} \right)\) \( \Rightarrow \dfrac{{SF}}{{SE}} = \dfrac{{SG}}{{SA}}\) \( \Rightarrow SG = \dfrac{{SA.SF}}{{SE}} = \dfrac{{b.\dfrac{b}{2}}}{h} = \dfrac{{{b^2}}}{{2h}}\). Vậy bán kính mặt cầu ngoại tiếp khối chóp \(S.ABC\) là \(R = SG = \dfrac{{{b^2}}}{{2h}}\). Chọn C. Câu hỏi 6 : Cho tứ diện \(ABCD\) có cạnh \(AD\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), tam giác \(ABC\) vuông tại \(B\) có cạnh \(AB = 3\), \(BC = 4\)và góc giữa \(DC\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích mặt cầu ngoại tiếp tứ diện.
Đáp án: C Phương pháp giải: - Chứng minh tam giác \(BCD\) vuông tại \(B\), từ đó tìm tâm mặt cầu ngoại tiếp tứ diện. - Xác định góc giữa \(DC\) và \(\left( {ABC} \right)\) là góc giữa \(DC\) và hình chiếu của \(DC\) lên \(\left( {ABC} \right)\). - Sử dụng định lí Pytago, tính chất tam giác vuông cân tính bán kính mặt cầu. - Tính thể tích khối cầu có bán kính R là : \(V = \dfrac{4}{3}\pi {R^3}\). Lời giải chi tiết:
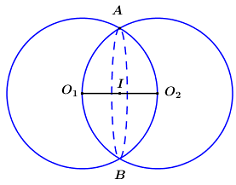
Ta có : \(\left\{ \begin{array}{l}BC \bot BA\\BC \bot DA\end{array} \right. \Rightarrow BC \bot \left( {ABD} \right)\)\( \Rightarrow BC \bot BD\)\( \Rightarrow \Delta BCD\) vuông tại B. Gọi I là trung điểm của CD thì \(IB = IC = ID = \dfrac{1}{2}CD\). Tam giác ACD vuông tại A nên \(IA = IC = ID = \dfrac{1}{2}CD\). Do đó \(IA = IB = IC = ID \Rightarrow I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\). Tam giác ABC vuông tại B nên \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {4^2}} = 5\) (Định lí Pytago). Vì \(DA \bot \left( {ABC} \right)\) nên \(AC\) là hình chiếu của \(DC\) lên \(\left( {ABC} \right)\). \( \Rightarrow \angle \left( {DC;\left( {ABC} \right)} \right) = \angle \left( {DC;AC} \right) = \angle DCA = {45^0}\). Tam giác \(DAC\) vuông tại \(A\) có \(\widehat {DCA} = {45^0}\) nên là tam giác vuông cân \( \Rightarrow DC = AC\sqrt 2 = 5\sqrt 2 \). \( \Rightarrow R = IA = \dfrac{1}{2}DC = \dfrac{{5\sqrt 2 }}{2}\). Vậy thể tích khối cầu ngoại tiếp tứ diện \(ABCD\) là : \(V = \dfrac{4}{3}\pi I{A^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{5\sqrt 2 }}{2}} \right)^3} = \dfrac{{125\sqrt 2 }}{3}\pi \). Chọn C. Câu hỏi 7 : Cho hai khối cầu \(\left( {{S_1}} \right),\,\,\left( {{S_2}} \right)\) có cùng bán kính 2 thỏa mãn tính chất: tâm của \(\left( {{S_1}} \right)\) thuộc \(\left( {{S_2}} \right)\) và ngược lại. Tính thể tích phần chung V của hai khối cầu tạo bởi \(\left( {{S_1}} \right)\) và \(\left( {{S_2}} \right)\).
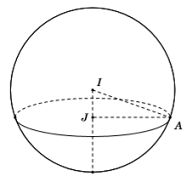
Đáp án: A Phương pháp giải: Sử dụng công thức tính thể tích khối chỏm cầu bán kính R, chiều cao h là \(V = \pi {h^2}\left( {R - \dfrac{h}{3}} \right)\). Lời giải chi tiết:
Gọi \({O_1},\,\,{O_2}\) lần lượt là tâm mặt cầu \(\left( {{S_1}} \right),\,\,\left( {{S_2}} \right)\). Hai mặt cầu này cắt nhau theo giao tuyến là đường tròn (C) có tâm I. Gọi A, B là một đường kính của đường tròn giao tuyến như hình vẽ, ta có AB là trung trực của \({O_1}{O_2}\), do đó I là trung điểm của \({O_1}{O_2}\) \( \Rightarrow I{O_1} = I{O_2} = \dfrac{1}{2}{O_1}{O_2} = \dfrac{R}{2} = 1\). Thể tích phần chung chính là tổng thể tích của hai khối chỏm cầu bằng nhau có bán kính R = 2, chiều cao \(h = \dfrac{R}{2} = 1\). Vậy \(V = 2.\pi {h^2}\left( {R - \dfrac{h}{3}} \right) = 2\pi {.1^2}\left( {2 - \dfrac{1}{3}} \right) = \dfrac{{10\pi }}{3}\). Chọn A. Câu hỏi 8 : Cho mặt cầu \(\left( S \right)\) tâm \(O\) và các điểm \(A\), \(B\), \(C\) nằm trên mặt cầu \(\left( S \right)\) sao cho \(AB = 3\), \(AC = 4\), \(BC = 5\) và khoảng cách từ \(O\) đến mặt phẳng \(\left( {ABC} \right)\) bằng \(1\). Thể tích của khối cầu \(\left( S \right)\) bằng
Đáp án: C Phương pháp giải: - Xác định chiều cao hạ từ tâm O của mặt cầu xuống mặt phẳng ABC. - Tính bán kính của mặt cầu R = OA. - Áp dụng công thức tính thể tích khối cầu bán kính R là: \(V = \dfrac{4}{3}\pi {R^3}.\) Lời giải chi tiết:
Tam giác ABC có: \(\left\{ \begin{array}{l}A{B^2} + A{C^2} = {3^2} + {4^2} = 25\\B{C^2} = {5^2} = 25\end{array} \right.\) \( \Rightarrow A{B^2} + A{C^2} = B{C^2}\) \( \Rightarrow \Delta ABC\) vuông tại A (Định lí Pytago đảo). Gọi H là trung điểm của BC khi đó H là tâm đường tròn ngoại tiếp tam giác ABC, suy ra \(HA = HB = HC = \dfrac{1}{2}BC = \dfrac{5}{2}.\) Mà \(OA = OB = OC \Rightarrow OH \bot \left( {ABC} \right)\)\( \Rightarrow d\left( {O;\left( {ABC} \right)} \right) = OH = 1.\). Áp dụng định lí Pytago trong tam giác vuông OBH có: \(R = OB = \sqrt {O{H^2} + H{B^2}} = \sqrt {1 + {{\left( {\dfrac{5}{2}} \right)}^2}} = \dfrac{{\sqrt {29} }}{2}.\) Vậy thể tích khối cầu cần tìm là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{{29\sqrt {29} }}{6}\pi .\) Chọn C. Câu hỏi 9 : Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AA’ = 2a, BC = a. Gọi M là trung điểm BB’. Bán kính mặt cầu ngoại tiếp khối chóp M.A’B’C’ bằng:
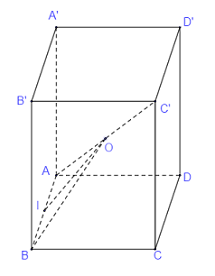
Đáp án: C Phương pháp giải: - Gọi \(O,\,\,O'\) lần lượt là tâm tam giác đều ABC và A’B’C’, khi đó ta có OO’ là trục của (A’B’C’). Gọi N là trung điểm của B’M, E là trung điểm của A’C’, qua N kẻ NI // B’E \(\left( {I \in OO'} \right)\), chứng minh \(IA' = IB' = IC' = IM\). - Sử dụng định lí Pytago tính bán kính mặt cầu. Lời giải chi tiết:
Gọi \(O,\,\,O'\) lần lượt là tâm tam giác đều ABC và A’B’C’, khi đó ta có OO’ là trục của (A’B’C’). Gọi N là trung điểm của B’M, E là trung điểm của A’C’. Qua N kẻ NI // B’E \(\left( {I \in OO'} \right)\) ta có: \(\left\{ \begin{array}{l}B'E \bot BB'\\NI\parallel B'E\end{array} \right. \Rightarrow NI \bot BB'\) \( \Rightarrow IM = IB'\). Lại có \(I \in OO'\) nên \(IA' = IB' = IC'\). Do đó ta có \(IA' = IB' = IC' = IM\) nên I là tâm mặt cầu ngoại tiếp chóp M.A’B’C’, bán kính \(R = IB'\). Ta có: \(\left\{ \begin{array}{l}NI\parallel B'O'\\B'N\parallel O'I\end{array} \right.\) nên O’B’NI là hình bình hành \( \Rightarrow O'I = B'N = \dfrac{1}{2}B'M = \dfrac{1}{4}BB' = \dfrac{a}{2}\). Tam giác A’B’C’ đều cạnh a nên \(B'E = \dfrac{{a\sqrt 3 }}{2} \Rightarrow B'O = \dfrac{2}{3}B'E = \dfrac{{a\sqrt 3 }}{3}\). Áp dụng định lí Pytago trong tam giác vuông O’B’I có: \(IB' = \sqrt {O'{I^2} + B'O{'^2}} = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{a\sqrt {21} }}{6}\). Chọn C. Câu hỏi 10 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) và \(BC = a.\) Cạnh bên \(SA\) vuông góc với đáy \(\left( {ABC} \right).\) Gọi \(H,{\rm{ }}K\) lần lượt là hình chiếu vuông góc của \(A\) lên \(SB\) và \(SC.\) Thể tích của khối cầu ngoại tiếp hình chóp \(A.HKCB\) bằng
Đáp án: B Phương pháp giải: - Xác định vị trí tâm mặt cầu ngoại tiếp khối chóp – là điểm cách đều các đỉnh của khối chóp. - Tính bán kính \(R\) của khối cầu. - Tính thể tích khối cầu bán kính \(R\): \(V = \dfrac{4}{3}\pi {R^3}\). Lời giải chi tiết:
Gọi \(O\) là trung điểm của \(AC\). Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\). Ta có: \(\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot HC\) \( \Rightarrow \Delta AHC\) vuông tại \(H\) \( \Rightarrow H\) thuộc mặt cầu tâm \(O\) đường kính \(AC\). Ta lại có: \(\Delta AKC,\,\,\Delta ABC\) lần lượt vuông tại \(K,\,\,B\) \( \Rightarrow K,\,\,B\) thuộc thuộc mặt cầu tâm \(O\) đường kính \(AC\). \( \Rightarrow \) 5 điểm \(A,\,\,H,\,\,K,\,\,B,\,\,C\) đều thuộc mặt cầu tâm \(O\) đường kính AC hay khối chóp \(A.HKCB\) nội tiếp mặt cầu tâm \(O\) đường kính \(AC\). Khi đó bán kính mặt cầu là \(R = \dfrac{{AC}}{2}\). Tam giác \(ABC\) vuông cân tại \(B\) và \(BC = a \Rightarrow AC = a\sqrt 2 \)\( \Rightarrow R = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\). Vậy thể tích của khối cầu ngoại tiếp hình chóp \(A.HKCB\) bằng \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^3} = \dfrac{{\pi {a^3}\sqrt 2 }}{3}\). Chọn B. Câu hỏi 11 : Cho mặt cầu \(\left( S \right)\). Biết rằng khi cắt mặt cầu \(\left( S \right)\) bởi một mặt phẳng cách tâm một khoảng có độ dài là 3 thì được giao tuyến là đường tròn \(\left( T \right)\) có chu vi là \(12\pi\). Diện tích của mặt cầu \(\left( S \right)\) bằng:
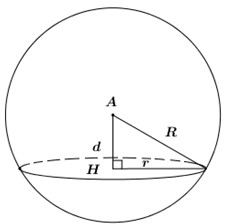
Đáp án: A Phương pháp giải: - Tính bán kính của đường tròn giao tuyến \(\left( T \right)\), sử dụng công thức chu vi đường tròn có bán kính \(r\) là \(C = 2\pi r\) - Sử dụng định lí Pytago tính bán kính mặt cầu \(\left( S \right)\): \(R = \sqrt {{r^2} + {d^2}} \) với \(d\) là khoảng cách từ tâm của mặt cầu \(\left( S \right)\) đến mặt phẳng chứa đường tròn \(\left( T \right)\). - Diện tích mặt cầu bán kính \(R\) là: \(S = 4\pi {R^2}\). Lời giải chi tiết:
Gọi \(I,\,\,J\) theo thứ tự là tâm mặt cầu \(\left( S \right)\) và đường tròn \(\left( T \right)\), \(A\) là điểm bất kì thuộc đường tròn \(\left( T \right)\). Khi đó ta có \(IJ = 3\), \(2\pi .AJ = 12\pi \Leftrightarrow AJ = 6\). Áp dụng định lí Pytago trong tam giác vuông \(AIJ\) ta có: \(AI = \sqrt {A{J^2} + I{J^2}} = \sqrt {{6^2} + {3^2}} = 3\sqrt 5 \). \( \Rightarrow \) Bán kính của mặt cầu là \(R = 3\sqrt 5 \). Vậy diện tích mặt cầu \(\left( S \right)\) là: \(S = 4\pi {R^2} = 4\pi .{\left( {3\sqrt 5 } \right)^2} = 180\pi .\) Chọn A. Câu hỏi 12 : Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), tam giác \(ABC\) vuông tại \(B\). Biết \(SA = 2a\), \(AB = a\), \(BC = a\sqrt 3 \). Tính bán kính \(R\) của mặt cầu ngoại tiếp hình chóp đã cho.
Đáp án: A Phương pháp giải: - Tam giác vuông có tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền. - Xác định điểm cách đều cả 4 đỉnh của chóp. - Sử dụng định lí Pytago để tính bán kính mặt cầu ngoại tiếp khối chóp. Lời giải chi tiết:
Gọi \(O,\,\,I\) lần lượt là trung điểm của \(AC\) và \(SC\). Khi đó \(OI\) là đường trung bình của tam giác \(SAC\) nên \(OI\parallel SA\). Mà \(SA \bot \left( {ABC} \right) \Rightarrow OI \bot \left( {ABC} \right)\). Tam giác \(ABC\) vuông tại \(B\) nên \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\), mà \(OI \bot \left( {ABC} \right)\) nên \(OI\) chính là trục của \(\left( {ABC} \right)\), suy ra \(IA = IB = IC\,\,\,\left( 1 \right)\). Lại có \(SA \bot \left( {ABC} \right)\) nên \(SA \bot AC\), do đó tam giác \(SAC\) vuông tại \(A\) nên \(I\) chính là tâm đường tròn ngoại tiếp tam giác \(SAC\), suy ra \(IS = IA = IC\,\,\,\left( 2 \right)\). Từ (1) và (2) ta có \(IA = IB = IC = IS\), hay \(I\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\), và bán kính mặt cầu là \(R = IS = \dfrac{1}{2}SC\). Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = 2a\). Áp dụng định lí Pytago trong tam giác vuông \(SAC\) ta có: \(SC = \sqrt {S{A^2} + A{C^2}} = 2a\sqrt 2 \). Vậy \(R = \dfrac{1}{2}SC = a\sqrt 2 \). Chọn A. Câu hỏi 13 : Một thùng rượu vang có dạng hình tròn xoay có hai đáy là hai hình tròn bằng nhau, khoảng cách giữa hai đáy bằng \(80\left( {cm} \right)\). Đường sinh của mặt xung quanh thùng là một phần đường tròn có bán kính \(60\left( {cm} \right)\)(tham khảo hình minh họa bên). Hỏi thùng đó có thể đựng bao nhiêu lít rượu?(làm tròn đến hàng đơn vị)
Đáp án: A Phương pháp giải: Áp dụng công thức tính chỏm cầu \({V_{cc}} = \pi {h^2}\left( {R - \dfrac{h}{3}} \right)\), với \(R\) là bán khối cầu, h là chiều cao của chỏm cầu. Lời giải chi tiết:
Ta có đường kính mặt cầu là \(60.2 = 120\,\,\,\left( {cm} \right).\) Mà khoảng cách giữa hai đáy của thùng rượu là \(80cm\) Nên chiều cao chỏm cầu là \(h = \dfrac{{120 - 80}}{2} = 20\,\,\left( {cm} \right).\) Thế tích của 1 chỏm cầu chiều cao \(h = 20\) và bán kính \(60cm\)là \({V_{cc}} = \pi {h^2}\left( {R - \dfrac{h}{3}} \right) = \pi {.20^2}\left( {60 - \dfrac{{20}}{3}} \right) = \dfrac{{64000}}{3}\pi \,\,\left( {c{m^3}} \right) = \dfrac{{64\pi }}{3}\,\,\left( l \right)\) Thể tích của cả khối cầu bán kính 60 cm là \(V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {.60^3} = 288000\pi \,\,\left( {c{m^3}} \right) = 288\pi \,\,\left( l \right)\) Khi đó thể tích thùng rượu là \(V' = V - 2{V_{cc}} = \dfrac{{736}}{3}\pi \,\,\left( l \right) \approx 771\,\,\left( l \right).\) Chọn A. Câu hỏi 14 : Cho lăng trụ đứng ABC.A'B'C' có chiều cao bằng 4, đáy ABC là tam giác cân tại A với AB = AC = 2; \(\angle BAC = {120^0}\). Tính diện tích mặt cầu ngoại tiếp lăng trụ trên.
Đáp án: C Phương pháp giải: - Gọi M là trung điểm của BC, H là điểm đối xứng với A qua M. Chứng minh H là tâm đường tròn ngoại tiếp tam giác ABC. - Gọi H’ là hình chiếu của A lên (A’B’C’), gọi I là trung điểm của HH’, chứng minh I là tâm mặt cầu ngoại tiếp khối lăng trụ đứng. - Sử dụng định lí Pytago tính bán kính mặt cầu. - Sử dụng công thức tính diện tích mặt cầu bán kính R là \({S_{mc}} = 4\pi {R^2}\). Lời giải chi tiết:
Gọi M là trung điểm của BC, H là điểm đối xứng với A qua M. Xét tứ giác ABHC có hai đường chéo cắt nhau tại trung điểm mỗi đường và \(AM \bot BC \Rightarrow AH \bot BC\) (do tam giác ABC cân tại A) nên ABHC là hình thoi \( \Rightarrow HB = HC\). Xét tam giác ABH có AB = BH, \(\angle BAH = \dfrac{1}{2}\angle BAC = {60^0}\) nên là tam giác đều, do đó HA = HB. Suy ra HA = HB = HC hay H là tâm đường tròn ngoại tiếp tam giác ABC. Gọi H’ là hình chiếu của A lên (A’B’C’) thì H’ chính là tâm đường tròn ngoại tiếp tam giác A’B’C’, khi đó HH’ là trục của khối lăng trụ đứng. Gọi I là trung điểm của HH’, ta có IA = IB = IC, IA’ = IB’ = IC’. Xét tam giác vuông AHI và tam giác vuông A’H’I có: HI = H’I (theo cách dựng), AH = A’H’. \( \Rightarrow \Delta AHI = \Delta A'H'I\) (2 cạnh góc vuông) \( \Rightarrow IA = IA'\). Do đó A = IB = IC = IA’ = IB’ = IC’ hay I chính là tâm mặt cầu ngoại tiếp khối lăng trụ đứng ABC.A’B’C’. Ta có AH = AB = 2 (do ABHC là hình thoi) và HH’ = AA’ = 4 nên IH = 2. Áp dụng định lí Pytago trong tam giác vuông AHI có: \(AI = \sqrt {A{H^2} + H{I^2}} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \). Suy ra bán kính mặt cầu ngoại tiếp khối lăng trụ là \(R = 2\sqrt 2 \). Vậy diện tích mặt cầu ngoại tiếp khối lăng trụ là: \({S_{mc}} = 4\pi {R^2} = 4\pi .{\left( {2\sqrt 2 } \right)^2} = 32\pi \). Chọn C. Câu hỏi 15 : Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\), \(AB = \sqrt 3 \), \(AC = 2\) và \(\angle BAC = {30^0}\). Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Bán kính R của mặt cầu ngoại tiếp hình chóp A.BCNM là:
Đáp án: C Phương pháp giải: - Sử dụng định lí Cô-sin trong tam giác tính độ dài cạnh BC, từ đó sử dụng định lí Pytago đảo chứng minh \(\Delta ABC\) vuông tại B. - Gọi I là trung điểm AC, chứng minh IA = IB = IC = IM = IN và suy ra bán kính mặt cầu. Lời giải chi tiết:
Áp dụng định lí Cosin trong tam giác ABC ta có: \(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \angle BAC\\B{C^2} = {\left( {\sqrt 3 } \right)^2} + {2^2} - 2.\sqrt 3 .2.\dfrac{{\sqrt 3 }}{2} = 1\\ \Rightarrow BC = 1\\ \Rightarrow A{B^2} + B{C^2} = A{C^2}\end{array}\) \( \Rightarrow \Delta ABC\) vuông tại B (Định lí Pytago đảo). Gọi I là trung điểm của AC \( \Rightarrow I\) là tâm đường tròn ngoại tiếp tam giác ABC, do đó có IA = IB = IC (1). Gọi H là trung điểm của AB ta có: \(IH \bot AB\). Ta có: \(\left\{ \begin{array}{l}IH \bot AB\\IH \bot SA\end{array} \right. \Rightarrow IH \bot \left( {SAB} \right) \Rightarrow IH \bot \left( {ABM} \right)\). Lại có \(\Delta ABM\) vuông tại M, có H là trung điểm của cạnh huyền AB nên H là tâm đường tròn ngoại tiếp \(\Delta ABM\) \( \Rightarrow IH\) là trục của \(\left( {ABM} \right)\) \( \Rightarrow IA = IB = IM\) (2). \(\Delta ACN\) vuông tại N có I là trung điểm cạnh huyền BC nên IA = IC = IN (3) Từ (1), (2), (3) ta suy ra IA = IB = IC = IM = IN hay I là tâm mặt cầu ngoại tiếp khối chóp A.BCNM, bán kính khối cầu là R = IA \( = \dfrac{1}{2}AC = 1\). Chọn C. Câu hỏi 16 : Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), tam giác \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\) bằng:
Đáp án: A Phương pháp giải: Xác định trục đường tròn ngoại tiếp tam giác \(SAB\) và trục đường tròn ngoại tiếp tứ giác \(ABCD\). Giao hai trục là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\) Từ đó tính bán kính dựa vào định lý Pytago Lời giải chi tiết: Gọi \(H\) là trung điểm đoạn \(AB\) và \(E\) là giao điểm hai đường chéo. Vì \(\Delta SAB\) đều nên \(SH \bot AB \Rightarrow SH \bot \left( {ABCD} \right)\) (vì \(\left( {SAB} \right) \bot \left( {ABCD} \right)\)) Ta có \(\left\{ \begin{array}{l}EH \bot AB\\EH \bot SH\end{array} \right. \Rightarrow EH \bot \left( {SAB} \right)\) Gọi I là trọng tâm tam giác \(SAB\), qua \(I\) kẻ \(Ix//HE\) Qua \(E\) kẻ \(Ey//SH\), và \(Ey\) giao với \(Ix\) tại \(K\). Khi đó \(KS = KA = KB = KC = KD.\) Hay \(K\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\) Ta có \(\Delta IKS\) vuông tại \(I\) có \(IS = \dfrac{2}{3}SH = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\) ; \(HE = \dfrac{{BC}}{2} = \dfrac{a}{2}.\) Nên \(KS = \sqrt {S{I^2} + I{K^2}} \) \( = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt {21} }}{6}\) Chọn A. Câu hỏi 17 : Cho hình chóp \(D.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(DA\) vuông góc với mặt phẳng đáy. Biết \(AB = 3a,\,\,BC = 4a,\,\,AD = 5a\). Bán kính mặt cầu ngoại tiếp hình chóp \(D.ABC\) bằng:
Đáp án: D Phương pháp giải: Cách tìm tâm mặt cầu ngoại tiếp hình chóp: +) Tìm tâm đường tròn ngoại tiếp đa giác đáy (Vì vậy, hình chóp có mặt cầu ngoại tiếp khi có đường tròn ngoại tiếp đa giác đáy). +) Dựng đường thẳng \(d\) qua tâm đường tròn ngoại tiếp và vuông góc với mặt phẳng đáy. +) Dựng mặt phẳng \(\left( \alpha \right)\) là mặt phẳng trung trực của một cạnh bên bất kì. +) Giao điểm của \(d\) và mp\(\left( \alpha \right)\) là tâm mặt cầu ngoại tiếp khối chóp đã cho. Lời giải chi tiết:
Gọi \(M\) và \(I\) lần lượt là trung điểm của \(AC,\,\,DC.\) Tam giác \(ABC\) vuông tại \(B\) nên trung điểm \(M\) của \(AC\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). \(M,\,\,I\) lần lượt là trung điểm của \(AC,\,\,DC\) nên \(MI\) là đường trung bình trong \(\Delta ADC\) hay \(MI\parallel AD\). Mặt khác, theo giả thiết \(DA \bot \left( {ABC} \right) \Rightarrow MI \bot \left( {ABC} \right)\). Mà \(M\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) và \(MI \bot \left( {ABC} \right)\) nên \(MI\) là trục của tam giác \(ABC\) hay \(IA = IB = IC\). Vì \(DA \bot \left( {ABC} \right) \Rightarrow DA \bot AC\) Tam giác \(DAC\) vuông tại \(A\) nên \(I\) là tâm đường tròn ngoại tiếp tam giác hay \(IA = ID = IC\). Do đó, \(IA = IB = IC = ID\) hay \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(D.ABC\). Tam giác \(ABC\) vuông tại \(B\) nên \(A{C^2} = A{B^2} + B{C^2} \Rightarrow AC = 5a\). Tam giác \(DAC\) vuông tại \(A\) nên \(CD = \sqrt {A{D^2} + A{C^2}} = 5\sqrt 2 a\). Vậy bán kính của mặt cầu ngoại tiếp khối chóp là \(R = IA = \dfrac{1}{2}DC = \dfrac{{5\sqrt 2 a}}{2}.\) Chọn D. Câu hỏi 18 : Cho 2 đường tròn nằm trên 2 mặt phẳng phân biệt và có chung dây cung \(AB\). Có bao nhiêu mặt cầu chứa cả 2 đường tròn đó?
Đáp án: B Phương pháp giải: Xác định số lượng tâm, bán kính của mặt cầu. Lời giải chi tiết:
Gọi tâm của 2 đường tròn là \(H,\,\,K\) và \(I\) là tâm của mặt cầu chứa cả 2 đường tròn đó. Nhận xét: \(I\) chính là giao điểm của hai đường vuông góc kẻ từ tâm các đường tròn, vuông góc với mặt phẳng chứa đường tròn đó. Do đó, tâm \(I\)được xác định là duy nhất. Vì 2 đường tròn nằm trên có chung dây cung AB nên AB cũng là 1 dây cung của mặt cầu. \( \Rightarrow \) Ta xác định được 1 mặt cầu duy nhất có tâm I và đi qua các điểm A, B. Chọn B. Câu hỏi 19 : Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9. Khối chóp có thể tích V lớn nhất bằng:
Đáp án: D Phương pháp giải: Lời giải chi tiết:
Giả sử khối chóp đó là S.ABCD. Ta có hình vẽ bên: Ta có: \(R = \dfrac{{S{A^2}}}{{2.SH}} = 9 \Rightarrow \dfrac{{S{H^2} + A{H^2}}}{{SH}} = 18 \Leftrightarrow A{H^2} = 18.SH - S{H^2}\) Mặt khác: \({V_{S.ABCD}} = \dfrac{1}{3}.SH.{S_{ABCD}} = \dfrac{1}{3}.SH.\dfrac{{A{C^2}}}{2} = \dfrac{2}{3}.SH.A{H^2} = \dfrac{2}{3}.SH.\left( {18.SH - S{H^2}} \right)\) Xét hàm số \(f\left( t \right) = \dfrac{2}{3}{t^2}\left( {18 - t} \right) = \dfrac{8}{3}.\left( {\dfrac{t}{2}.\dfrac{t}{2}.\left( {18 - t} \right)} \right) \le \dfrac{8}{3}{\left( {\dfrac{{t + 18 - t}}{3}} \right)^3} = 576\,\,\left( {0 < t < 18} \right)\) Dấu “=” xảy ra khi và chỉ khi \(\dfrac{t}{2} = 18 - t \Leftrightarrow t = 12\) Suy ra, thể tích khối chóp S.ABCD đạt giá trị lớn nhất là 576 khi và chỉ khi \(SH = 12\). Chọn D. Câu hỏi 20 : Cho hình vuông \(ABCD\) cạnh \(4a\). Trên cạnh \(AB\) và \(AD\) lần lượt lấy 2 điểm \(H\) và \(K\) sao cho \(BH = 3HA\) và \(AK = 3KD\). Trên đường thẳng vuông góc với \(\left( {ABCD} \right)\) tại \(H\) lấy điểm \(S\) sao cho \(\angle SBH = {30^0}\). Gọi \(E\) là giao điểm của \(CH\) và \(BK\). Tính thể tích của khối cầu ngoại tiếp của hình chóp \(S.AHEK\).
Đáp án: A Phương pháp giải: - Chứng minh tứ giác \(AHEK\) nội tiếp đường tròn đường kính \(HK\). - Xác định trục của tứ giác \(AHEK\), cắt đường trung trực của \(SH\) tại \(M\). - Chứng minh \(M\) là tâm mặt cầu ngoại tiếp chóp \(S.AHEK\). - Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông và định lí Pytago để tính bán kính mặt cầu. - Thể tích khối cầu bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\). Lời giải chi tiết:
Xét \(\Delta HBC\) và \(\Delta KAB\) có: \(\angle HBC = \angle KAB = {90^0}\); \(HB = KA = 3a\); \(BC = AB = 4a\). \( \Rightarrow \Delta HBC = \Delta KAB\,\,\,\left( {c.g.c} \right)\) \( \Rightarrow \angle HCB = \angle KBA\) (hai góc tương ứng). Mà \(\angle KBA + \angle KBC = {90^0}\) nên \(\angle KBC + \angle HCB = {90^0}\), do đó tam giác \(EBC\) vuông tại \(E\) hay \(BK \bot HC\). Gọi \(I\) là trung điểm của \(HK\), ta có: \(\angle HAK = \angle HEK = {90^0}\), do đó \(AHEK\) là tứ giác nội tiếp đường tròn tâm \(I\) đường kính \(HK\). Trong \(\left( {SHK} \right)\) kẻ đường thẳng song song với \(SH\) cắt \(SK\) tại \(M\), ta có: \(\left\{ \begin{array}{l}SH \bot \left( {ABCD} \right)\\d\parallel SH\end{array} \right. \Rightarrow d \bot \left( {ABCD} \right) \Rightarrow d \bot \left( {AHEK} \right)\) tại \(I\), mà \(I\) là tâm đường tròn ngoại tiếp tứ giác \(AHEK\) nên \(MA = MH = ME = MK\,\,\,\left( 1 \right)\). Xét tam giác \(SHK\) có: \(I\) là trung điểm của \(HK\). \(IM\parallel SH\) (theo cách dựng) \( \Rightarrow M\) là trung điểm của \(SK\) (định lí đường trung bình của tam giác). Mà \(SH \bot \left( {ABCD} \right)\) nên \(SH \bot HK\), suy ra tam giác \(SHK\) vuông tại \(H\), do đó \(M\) là tâm đường tròn ngoại tiếp tam giác \(SHK\) hay \(MS = MH = MK\,\,\,\left( 2 \right)\). Từ (1) và (2) \( \Rightarrow MA = MH = ME = MK = MS\), suy ra \(M\) là tâm khối cầu ngoại tiếp \(S.AHEK\), bán kính khối cầu là \(R = \dfrac{{SK}}{2}.\) Tam giác \(SHB\) vuông tại \(H\) có \(BH = 3a\), \(\angle SBH = {30^0}\,\,\left( {gt} \right)\) nên \(SH = HB.tan{30^0} = 3a.\dfrac{{\sqrt 3 }}{3} = a\sqrt 3 \). Áp dụng định lí Pytago ta có: \(\begin{array}{l}HK = \sqrt {A{H^2} + A{K^2}} = \sqrt {{a^2} + {{\left( {3a} \right)}^2}} = a\sqrt {10} \\SK = \sqrt {H{K^2} + S{H^2}} = \sqrt {{{\left( {\sqrt 3 a} \right)}^2} + {{\left( {\sqrt {10} a} \right)}^2}} = a\sqrt {13} \\ \Rightarrow R = \dfrac{{SK}}{2} = \dfrac{{a\sqrt {13} }}{2}\end{array}\) Vậy thể tích khối cầu ngoại tiếp chóp \(S.AHEK\) là: \(V = \dfrac{4}{3}.\pi .{R^3} = \dfrac{4}{3}\pi {\left( {\frac{{a\sqrt {13} }}{2}} \right)^3} = \dfrac{{13\pi {a^3}\sqrt {13} }}{6}.\) Chọn A. Câu hỏi 21 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với \(AB = 3a,BC = 4a,SA \bot \left( {ABC} \right),\)cạnh bên SC tạo với đáy góc \(60^\circ .\) Thể tích khối cầu ngoại tiếp tứ diện S.ABC là
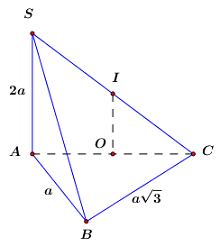
Đáp án: B Phương pháp giải: Tìm tâm mặt cầu ngoại tiếp tứ diện. Tính bán kính mặt cầu rồi tính thể tích dựa theo công thức \(V = \frac{4}{3}\pi {R^3}.\) Lời giải chi tiết: Gọi I là trung điểm của SC. Ta có \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\)vuông tại A Do đó \(IA = IS = IC\) Mặt khác \(BC \bot AB;BC \bot SA \Rightarrow BC \bot SB \Rightarrow \Delta SBC\) vuông tại B. Mà I là trung điểm của SC nên \(IS = IB = IC\) Suy ra I là tâm mặt cầu ngoại tiếp tứ diện S.ABC. +)\(\Delta ABC\) vuông tại B; có \(AB = 3;BC = 4\)\( \Rightarrow AC = 5\) +)\(\Delta SAC\) vuông tại A có \(AC = 5;\angle SCA = 60^\circ \Rightarrow SC = \frac{1}{{{\rm{cos60}}^\circ {\rm{.}}AC}} = 10\) Suy ra \(R = 5 \Rightarrow V = \frac{4}{3}\pi {R^3} = \frac{{500\pi {a^3}}}{3}.\) Chọn B. Câu hỏi 22 : Cho hình lập phương có cạnh \(4cm\). Mặt cầu tiếp xúc với 12 cạnh của hình lập phương đó có diện tích xung quanh là:
Đáp án: A Phương pháp giải: Mặt cầu tiếp xúc với 12 cạnh của hình lập phương, có tâm là tâm của hình lập phương, tiếp xúc với mỗi cạnh của hình lập phương tại trung điểm của nó. Tính bán kính của mặt cầu trên. Diện tích xung quanh của mặt cầu có bán kính \(R\) được tính bởi công thức \({S_{xq}} = 4\pi {R^2}\) Lời giải chi tiết:
Gọi hình lập phương đã cho là \(ABCD.A'B'C'D'\), \(O\) là giao điểm 2 đường chéo lớn hay \(O\) là tâm của hình lập phương. Gọi \(I\) là trung điểm \(AB\) Mặt cầu tiếp xúc với 12 cạnh của hình lập phương, có tâm là tâm của hình lập phương, tiếp xúc với mỗi cạnh của hình lập phương tại trung điểm của nó. Suy ra mặt cầu tiếp xúc với 12 cạnh của lập phương có tâm là \(O\) và bán kính \(R = OI\) \(I\) là trung điểm \(AB\) nên \(IA = IB = 2\left( {cm} \right)\) Ta có: \(AC' = \sqrt {AA{'^2} + A'C{'^2}} = \sqrt {AA{'^2} + A'B{'^2} + B'C{'^2}} = \sqrt 3 .4 = 4\sqrt 3 \) \( \Rightarrow AO = \dfrac{1}{2}AC' = 2\sqrt 3 \) \(OI \bot AB \Rightarrow OI = \sqrt {O{A^2} - A{I^2}} = \sqrt {{{\left( {2\sqrt 3 } \right)}^2} - {2^2}} = 2\sqrt 2 \left( {cm} \right)\) Suy ra diện tích xung quanh của mặt cầu trên là: \({S_{xq}} = 4\pi {R^2} = 4\pi .O{I^2} = 32\pi \left( {c{m^2}} \right)\) Chọn A Câu hỏi 23 : Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, \(AB = 2a,AD = a\), tam giác \(SAD\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(M\)là trung điểm của \(AB,\) \(H\) là hình chiếu vuông góc của \(D\) trên \(AC,\) \(I\) là trung điểm của \(HC.\) Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.MID.\)
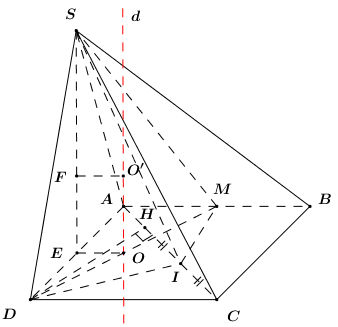
Đáp án: A Phương pháp giải: - Chứng minh tứ giác \(ADIM\) là tứ giác nội tiếp. Xác định tâm đường tròn ngoại tiếp tứ giác \(ADIM\). - Tâm mặt cầu ngoại tiếp chóp \(S.ADIM\) là giao điểm của hai trục của 2 mặt \(\left( {SAD} \right)\) và \(\left( {ADIM} \right)\). - Áp dụng tính chất tam giác đều và định lí Pytago tính bán kính mặt cầu ngoại tiếp chóp \(S.ADIM\). Lời giải chi tiết:
+ Xác định tâm mặt cầu ngoại tiếp chóp \(S.ADIM\). Áp dụng định lí Pytago trong tam giác vuông \(ACD\) có: \(AC = \sqrt {A{D^2} + C{D^2}} \)\( = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \). Áp dụng hệ thức lượng trong tam giác vuông \(ACD\) ta có \(AH.AC = A{D^2}\)\( \Rightarrow AH = \dfrac{{A{D^2}}}{{AC}} = \dfrac{{{a^2}}}{{a\sqrt 5 }} = \dfrac{{a\sqrt 5 }}{5}\). \( \Rightarrow HC = AC - AH = \dfrac{{4a\sqrt 5 }}{5}\)\( \Rightarrow IH = IC = \dfrac{{2a\sqrt 5 }}{5}\). \( \Rightarrow D{H^2} = AH.HC = \dfrac{{a\sqrt 5 }}{5}.\dfrac{{4a\sqrt 5 }}{5}\)\( \Rightarrow DH = \dfrac{{2a\sqrt 5 }}{5}\)\( = IH\). Áp dụng định lí Pytago trong tam giác vuông \(HDI\) có: \(DI = \sqrt {D{H^2} + H{I^2}} = \dfrac{{2a\sqrt {10} }}{5}\). Ta có: \(AI = AH + HI = \dfrac{{3a\sqrt 5 }}{5}\). Xét tam giác vuông \(ABC\) có: \(\cos \angle BAC = \dfrac{{AB}}{{AC}} = \dfrac{{2a}}{{a\sqrt 5 }} = \dfrac{2}{{\sqrt 5 }} = \cos \angle MAI\). Áp dụng định lí cosin trong tam giác \(AIM\) có; \(\begin{array}{l}M{I^2} = A{M^2} + A{I^2} - 2AM.AI.\cos \angle MAI\\M{I^2} = {a^2} + {\left( {\dfrac{{3a\sqrt 5 }}{5}} \right)^2} - 2.a.\dfrac{{3a\sqrt 5 }}{5}.\dfrac{2}{{\sqrt 5 }}\\M{I^2} = \dfrac{{2{a^2}}}{5} \Rightarrow MI = \dfrac{{a\sqrt {10} }}{5}\end{array}\) Áp dụng định lí Pytago trong tam giác vuông \(ADM\) có: \(DM = \sqrt {A{D^2} + A{M^2}} = a\sqrt 2 \). Xét tam giác \(DMI\) có \(D{M^2} = 2{a^2}\), \(D{I^2} + I{M^2} = {\left( {\dfrac{{2a\sqrt {10} }}{5}} \right)^2} + {\left( {\dfrac{{a\sqrt {10} }}{5}} \right)^2} = 2{a^2}\) \( \Rightarrow D{M^2} = D{I^2} + I{M^2}\)\( \Rightarrow \Delta DIM\) vuông tại \(I\)\( \Rightarrow \angle DIM = {90^0}\). Xét tứ giác \(ADIM\) có: \(\angle DAM = \angle DIM = {90^0}\). \( \Rightarrow A,\,\,I\) thuộc đường tròn đường kính \(DM\). Gọi \(O\) là trung điểm của \(DM\)\( \Rightarrow O\) là tâm đường tròn ngoại tiếp tứ giác \(ADIM\). Kẻ đường thẳng \(d\) qua \(O\) và \(d \bot \left( {ADIM} \right)\), suy ra \(d\) là trục của mặt phẳng \(\left( {ADIM} \right)\). Gọi \(E\) là trung điểm của \(AD \Rightarrow SE \bot AD\)\( \Rightarrow SE \bot \left( {ABCD} \right)\). Gọi \(F\) là tâm tam giác đều \(SAD\) . Qua \(F\) kẻ đường thẳng song song với \(OE\) cắt \(d\) tại \(O'\). Ta có: \(OE\) là đường trung bình của tam giác \(ADM\)\( \Rightarrow OE\parallel AM\)\( \Rightarrow OE \bot AB\). \(\left\{ \begin{array}{l}OE \bot AB\\OE \bot SE\end{array} \right. \Rightarrow OE \bot \left( {SAB} \right)\)\( \Rightarrow O'F \bot \left( {SAB} \right) \Rightarrow \)\(O'F\) là trục của \(\Delta SAB\). \( \Rightarrow O'S = O'A = O'B\). Lại có \(O' \in d \Rightarrow O'A = O'D = O'I = O'M\). \( \Rightarrow O'A = O'D = O'I = O'M = O'S\) \( \Rightarrow O'\) là tâm mặt cầu ngoại tiếp chóp \(S.ADIM\). + Tính \(R = O'S\). Tam giác \(SAD\) đều cạnh \(a\) \( \Rightarrow SE = \dfrac{{a\sqrt 3 }}{2}\)\( \Rightarrow SF = \dfrac{2}{3}SE = \dfrac{{a\sqrt 3 }}{3}\). \(EO\) là đường trung bình của tam giác \(ADM\)\( \Rightarrow EO = \dfrac{1}{2}AM = \dfrac{1}{2}a\)\( = O'F\). Áp dụng định lí Pytago trong tam giác vuông \(SFO'\) có: \(O'S = \sqrt {S{F^2} + O'{F^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt {21} }}{6}\). Vậy \(R = \dfrac{{a\sqrt {21} }}{6}\). Chọn A. Câu hỏi 24 : Cho lăng trụ đứng \(ABC.A'B'C'\) có \(BC = AB = a\), \(AC = a\sqrt 3 \). Biết \(B'C\) tạo với đáy góc \({60^0}\). Tính diện tích mặt cầu ngoại tiếp tứ diện \(AC'B'B\).
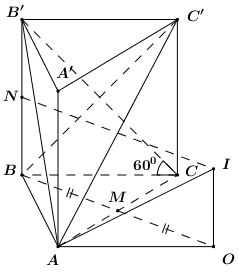
Đáp án: D Phương pháp giải: - Xác định tâm mặt cầu ngoại tiếp là điểm cách đều 4 đỉnh của tứ diện. - Áp dụng định lí Pytago để tính bán kính \(R\) của mặt cầu. - Diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}\). Lời giải chi tiết: Gọi \(M\) là trung điểm của \(AC\) và \(O\) là điểm đối xứng \(B\) qua \(M\). Ta có \(AM = MC = \frac{{a\sqrt 3 }}{2}\) và \(BM \bot AC\) (do tam giác \(ABC\) cân tại \(B\)). Áp dụng định lí Pytago trong tam giác vuông \(ABM\) có: \(BM = \sqrt {A{B^2} - A{M^2}} \) \( = \sqrt {{a^2} - \frac{{3{a^2}}}{4}} = \frac{a}{2}\). \( \Rightarrow OB = 2OM = a\). Xét tứ giác \(ABCO\) có: \(\left\{ \begin{array}{l}MA = MI\\MB = MO\\AC \bot OB\end{array} \right.\) \( \Rightarrow ABCO\) là hình thoi. \( \Rightarrow OA = OI = AB = BC = a\). \( \Rightarrow OA = OB = OC\) \( \Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Gọi \(N\) là trung điểm của \(BB'\), qua \(N\) kẻ mặt phẳng vuông góc với \(BB'\) cắt đường thẳng qua \(O\) và vuông góc với \(\left( {ABC} \right)\) tại \(I\) ta có: \(I\) thuộc đường thẳng qua \(O\) và vuông góc với \(\left( {ABC} \right)\) \( \Rightarrow IA = IB = IC\). \(I\) thuộc mặt phẳng vuông góc với \(BB'\) tại \(N\) \( \Rightarrow IB = IB'\). \( \Rightarrow IA = IB = IC = IB'\) \( \Rightarrow I\) thuộc trục của \(\left( {ABB'} \right)\), chính là trục của \(\left( {ABB'A'} \right)\). \( \Rightarrow IA = IB = IC = IB' = IA'\) \( \Rightarrow I\) thuộc trục của \(\left( {AA'C} \right)\), chính là trục của \(\left( {ACC'A'} \right)\). \( \Rightarrow IA = IB = IC = IB' = IA' = IC'\), do đó \(I\) chính là tâm mặt cầu ngoại tiếp tứ diện \(AC'B'B\). Ta có: \(BB' \bot \left( {ABC} \right)\)\( \Rightarrow \angle \left( {B'C;\left( {ABC} \right)} \right) = \angle \left( {B'C;BC} \right) = \angle B'CB = {60^0}\). \( \Rightarrow BB' = BC.\tan {60^0} = a\sqrt 3 \) \( \Rightarrow OI = BN = \frac{1}{2}BB' = \frac{{a\sqrt 3 }}{2}\). Áp dụng định lí Pytago trong tam giác vuông \(OAI\) có: \(IA = \sqrt {O{A^2} + O{I^2}} \) \( = \sqrt {{a^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{{a\sqrt 7 }}{2}\). \( \Rightarrow R = \frac{{a\sqrt 7 }}{2}\) \( \Rightarrow {S_{mc}} = 4\pi {R^2} = 7\pi {a^2}\). Chọn D. Câu hỏi 25 : Cho hình chóp \(SABC\) có đáy \(ABC\) là tam giác vuông tại \(B\) và \(BA = BC = 3.\) Cạnh bên \(SA = 6\) và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp đã cho.
Đáp án: D Phương pháp giải: Bán kính mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy, có chiều cao \(h\) và bán kính đường tròn ngoại tiếp đáy \({R_d}\) là: \(R = \sqrt {\dfrac{{{h^2} + 4R_d^2}}{4}} .\) Lời giải chi tiết: Ta có: \(\Delta ABC\) vuông cân tại \(B\) và \(AB = BC = 3\) \( \Rightarrow AC = AB\sqrt 2 = 3\sqrt 2 .\) \( \Rightarrow \) Bán kính đường tròn ngoại tiếp \(\Delta ABC\) là: \({R_d} = \dfrac{1}{2}AC = \dfrac{{3\sqrt 2 }}{2}.\) \( \Rightarrow \) Bán kính mặt cầu ngoại tiếp hình chóp \(SABC\) là: \(R = \sqrt {\dfrac{{S{A^2} + 4R_d^2}}{4}} = \sqrt {\dfrac{{{6^2} + 4.{{\left( {\dfrac{{3\sqrt 2 }}{2}} \right)}^2}}}{4}} = \dfrac{{3\sqrt 6 }}{2}.\) Chọn D. Câu hỏi 26 : Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Cạnh bên \(SA = a\sqrt 6 \) và vuông góc với đáy \(\left( {ABCD} \right)\). Tính theo \(a\) diện tích mặt cầu ngoại tiếp khối chóp \(S.ABCD\)
Đáp án: B Phương pháp giải: Tìm tâm mặt cầu ngoại tiếp khối chóp như sau: Tìm tâm đường tròn ngoại tiếp đa giác đáy. Qua tâm đường tròn đó, kẻ đường thẳng \(d\) vuông góc với mặt đáy cắt mặt phẳng trung trực của một cạnh bên bất kì tại \(I\). Khi đó, \(I\) chình là tâm mặt cầu ngoại tiếp khối chóp đã cho. Tính bán kính \(R\) của khối chóp. Diện tích mặt cầu có bán kính bằng \(R\) là \(S = 4\pi {R^2}\) Lời giải chi tiết:
Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(I\) là trung điểm của \(SC\). \(ABCD\) là hình vuông nên \(O\) là tâm đường tròn ngoại tiếp hình vuông \(ABCD\) và \(O\) là trung điểm \(AC\) và \(BD.\) \(OI\) là đường trung bình trong tam giác \(SAC\) nên \(OI//SA\) mà \(SA \bot \left( {ABCD} \right)\) nên \(OI \bot \left( {ABCD} \right)\) \(I\) nằm trên đường thẳng qua tâm \(O\) và vuông góc với mặt phẳng \(\left( {ABCD} \right)\) nên \(IA = IB = IC = ID\) Mặt khác tam giác \(SAC\) vuông tại \(A\) có trung tuyến \(AI\) nên \(IA = \dfrac{1}{2}SC = SI = IC\) Suy ra \(IS = IA = IB = IC = ID\) hay \(I\) là tâm mặt cầu ngoại tiếp khối chóp. Ta có: \(ABCD\) là hình vuông nên \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = \sqrt 2 a\) Tam giác \(SAC\) vuông tại \(A\) nên \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {6{a^2} + 2{a^2}} = 2\sqrt 2 a\) \( \Rightarrow R = \dfrac{1}{2}SC = \sqrt 2 a\) Diện tích của mặt cầu ngoại tiếp khối chóp là \(S = 4\pi {R^2} = 4\pi .{\left( {\sqrt 2 a} \right)^2} = 8\pi {a^2}\) Chọn B. Câu hỏi 27 : Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,\,AD = 2a,{\rm{AA}}' = 2a.\) Diện tích mặt cầu ngoại tiếp tứ diện \(ACB'D'\) bằng
Đáp án: D Phương pháp giải: - Gọi O là tâm hình hộp chữ nhật ABCD.A’B’C’D’, chứng minh O cũng chính là tâm mặt cầu ngoại tiếp tứ diện ACB’D’. - Tính bán kính R = OA. - Áp dụng công thức tính diện tích mặt cầu \(S = 4\pi {R^2}\). Lời giải chi tiết:
Gọi O là tâm hình hộp chữ nhật ABCD.A’B’C’D’, khi đó ta có OA = OC = OB’ = OD’. Khi đó O cũng chính là tâm mặt cầu ngoại tiếp tứ diện ACB’D’. Do đó bán kính mặt cầu ngoại tiếp tứ diện ACB’D’ là R = OA = \(\dfrac{1}{2}AC'\). Áp dụng định lí Pytago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \)\( = \sqrt {{a^2} + 4{a^2}} \)\( = a\sqrt 5 \). \(AC' = \sqrt {A{C^2} + AA{'^2}} \)\( = \sqrt {5{a^2} + 4{a^2}} \)\( = 3a\). Suy ra \(R = \dfrac{1}{2}AC' = \dfrac{{3a}}{2}\). Vậy diện tích mặt cầu ngoại tiếp tứ diện ACB’D’ là \(R = 4\pi {R^2}\)\( = 4\pi {\left( {\dfrac{{3a}}{2}} \right)^2}\)\( = 9\pi {a^2}\). Đáp án D. Câu hỏi 28 : Cho hình chóp đều \(S.ABCD\) có \(ABCD\) là hình vuông cạnh \(a,\) tam giác \(SAC\) vuông tại \(S.\) Bán kính mặt cầu ngoại tiếp hình chóp đều \(S.ABCD\) bằng
Đáp án: A Phương pháp giải: - Gọi O là giao điểm của AC và BD. Chứng minh OA = OB = OC = OD = OS. - Áp dụng định lí Pytago. Lời giải chi tiết:
Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên OA = OB = OC = OD. Tam giác SAC vuông tại S có SO là trung tuyến ứng với cạnh huyền AC nên \(SO = \dfrac{1}{2}AC\) = OA = OC. Suy ra OA = OB = OC = OD = OS nên O là tâm mặt cầu ngoại tiếp chóp S.ABCD và bán kính mặt cầu đó là R = OA. Áp dụng định lí Pytago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \)\( = \sqrt {{a^2} + {a^2}} \)\( = a\sqrt 2 \). Vậy \(R = \dfrac{{a\sqrt 2 }}{2} = \dfrac{a}{{\sqrt 2 }}\). Đáp án A. Câu hỏi 29 : Cho một hình nón đỉnh \(I\) có đường tròn đáy là đường tròn đường kính \(AB = 6cm\) và đường cao bằng \(3\sqrt 3 cm.\) Gọi \(\left( S \right)\) là mặt cầu chứa đỉnh \(I\) và đường tròn đáy của hình nón. Bán kính của mặt cầu \(\left( S \right)\) bằng
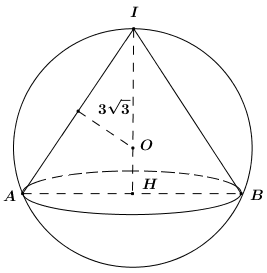
Đáp án: C Phương pháp giải: - Xác định tâm mặt cầu. - Chứng minh tâm mặt cầu trùng với tâm đường tròn ngoại tiếp tam giác IAB. - Chứng minh tam giác IAB đều. - Sử dụng công thức tính nhanh bán kính đường tròn ngoại tiếp tam giác đều cạnh a là \(R = \dfrac{{a\sqrt 3 }}{2}\). Lời giải chi tiết:
Mặt cầu chứa đỉnh I chứa đường tròn đường kính AB nên mặt cầu đi qua A, B. Do đó bán kính mặt cầu chính là bán kính đường tròn ngoại tiếp tam giác IBC. Tam giác IAB có IA = IB = l, suy ra tam giác IAB cân tại I. Gọi H là trung điểm của AB \( \Rightarrow SH \bot AB\) và AH = 3cm, \(IH = 3\sqrt 3 cm\). Áp dụng định lí Pytago trong tam giác vuông IAH ta có: \(IA = \sqrt {I{H^2} + A{H^2}} = \sqrt {27 + 9} = 6\,\,\left( {cm} \right) = IB\). \( \Rightarrow \Delta IAB\) đều cạnh 6cm. Vậy bán kính đường tròn ngoại tiếp tam giác IAB là \(R = \dfrac{{6\sqrt 3 }}{2} = 3\sqrt 3 \,\,\left( {cm} \right)\). Đáp án C. Câu hỏi 30 : Cho hàm số \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), cạnh vuông góc với mặt phẳng đáy. Biết \(SA = 10,\) \(AB = 6,\) \(BC = 8\). Bán kính của mặt cầu \(SA\)ngoại tiếp hình chóp bằng
Đáp án: C Phương pháp giải: Tìm tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\) bằng cách: - Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). - Qua \(O\) dựng đường thẳng \(d\) vuông góc với mặt phẳng \(\left( {ABC} \right)\). - Dựng mặt phẳng \(\left( \alpha \right)\) là mặt phẳng trung trực của một cạnh bên bất kì cắt đường thẳng \(d\) tại \(I\) thì \(I\) chính là tâm mặt cầu ngoại tiếp khối chóp. Suy ra bán kính của hình chóp \(R = IS = IA = IB = IC\). Lời giải chi tiết:
Gọi \(O\) là trung điểm \(AC\) và \(I\) là trung điểm \(SC\). Do tam giác \(ABC\) vuông tại \(B\) nên \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). \(IO\) là đường trung bình trong tam giác \(SAC\) nên \(IO\parallel SA\) mà \(SA \bot \left( {ABC} \right) \Rightarrow OI \bot \left( {ABC} \right)\). \(IO\) đi qua tâm đường tròn ngoại tiếp tam giác \(ABC\) và vuông góc với mp\(\left( {ABC} \right)\) nên \(IA = IB = IC\) (1) Mặt khác tam giác \(SAC\) vuông tại \(A,\) có trung tuyến \(AI\) nên \(AI = \dfrac{1}{2}SC = SI = IC\) (2) Từ (1) và (2) suy ra \(IA = IB = IC = IS\) do đó \(I\) là tâm mặt cầu ngoại tiếp khối chóp \(S.ABC\) Áp dụng định lí Pytago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{6^2} + {8^2}} = 10\) \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 \) Suy ra \(R = IA = \dfrac{1}{2}SC = \dfrac{1}{2}.10\sqrt 2 = 5\sqrt 2 \). Vậy bán kính mặt cầu ngoại tiếp hình chóp bằng \(5\sqrt 2 \). Chọn C. Câu hỏi 31 : Cho hình lập phương \(ABCD.A'B'C'D'\) có \(AC' = a\sqrt 3 \). Tính bán kính \(R\) của mặt cầu tiếp xúc với 6 mặt của hình lập phương trên
Đáp án: D Phương pháp giải: Mặt cầu tiếp xúc với 6 mặt của hình lập phương có đường kính lớn bằng cạnh của hình lập phương. Lời giải chi tiết:
\(ABCD.A'B'C'D'\) là hình lập phương nên ta có: \(\begin{array}{l}AC' = a\sqrt 3 \Leftrightarrow AC{'^2} = 3{a^2} \Leftrightarrow A{C^2} + CC{'^2} = 3{a^2}\\ \Leftrightarrow A{B^2} + B{C^2} + CC{'^2} = 3{a^2} \Leftrightarrow 3A{B^2} = 3{a^2} \Rightarrow AB = a\end{array}\) Mặt cầu tiếp xúc với 6 mặt của hình lập phương có đường kính lớn bằng cạnh của hình lập phương nên: \(2R = AB \Rightarrow R = \dfrac{a}{2}\). Vậy bán kính của mặt cầu tiếp xúc với 6 mặt của hình lập phương là \(R = \dfrac{a}{2}\). Chọn D. Câu hỏi 32 : Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng 4cm và chiều cao bằng 2cm . Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng
Đáp án: D Phương pháp giải: Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp đều có chiều cao \(h\), cạnh bên \(a\) là: \(R = \dfrac{{{a^2}}}{{2h}}\). Lời giải chi tiết: Hình chóp đều có chiều cao \(h = 2cm\), cạnh bên \(a = 4cm\) có bán kính mặt cầu ngoại tiếp là: \(R = \dfrac{{{a^2}}}{{2h}} = \dfrac{{{4^2}}}{{2.2}} = 4\,\,\left( {cm} \right)\). Chọn D. Câu hỏi 33 : Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), \(SA=a\), góc giữa hai mặt phẳng (SBC) và (ABC) bằng \(60^0\) . Biết mặt cầu tâm A bán kính \(\dfrac{{a\sqrt 3 }}{2}\) cắt mặt phẳng (SBC) theo giao tuyến là một đường tròn. Bán kính của đường tròn giao tuyến đó bằng:
Đáp án: A Phương pháp giải: - Sử dụng đạo hàm hợp tính đạo hàm hàm số \(g\left( x \right)\). - Giải phương trình \(g'\left( x \right) = 0\) và kết luận số cực trị của hàm số. Lời giải chi tiết:
Trong \(\left( {ABC} \right)\) kẻ \(AM \bot BC\,\,\left( {M \in BC} \right)\) ta có: \(\left\{ \begin{array}{l}BC \bot AM\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM\). Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SM \bot BC\\\left( {ABC} \right) \supset AM \bot BC\end{array} \right.\). \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SM;AM} \right) = \angle SMA = {60^0}\). Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AM \Rightarrow \Delta SAM\) vuông tại \(A\). Mà \(\widehat {SMA} = {60^0} \Rightarrow \widehat {ASM} = {30^0}\). Trong \(\left( {SAM} \right)\) kẻ \(AH \bot SM\), xét tam giác vuông \(SAH\) có: \(AH = SA.\sin {30^0} = \dfrac{a}{2}\). Ta có: \(\left\{ \begin{array}{l}AH \bot SM\\AH \bot BC\,\,\left( {BC \bot \left( {SAM} \right)} \right)\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right)\). \( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH = \dfrac{a}{2} = d\).
Giả sử mặt cầu tâm \(A\), bán kính \(R = \dfrac{{a\sqrt 3 }}{2}\) cắt \(\left( {SBC} \right)\) theo giao tuyến là một đường tròn có bán kính \(r\). Áp dụng định lí Pytago ta có: \(r = \sqrt {{R^2} - {d^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{2}\). Chọn A. Câu hỏi 34 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) và \(BA = BC = a.\) Cạnh bên \(SA = 2a\) và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp\(S.ABC\) là :
Đáp án: D Phương pháp giải: Xác định điểm cách đều bốn đỉnh của hình chóp từ đó tính bánh kính mặt cầu ngoại tiếp hình chóp Lời giải chi tiết:
Gọi \(D\) và \(E\) lần lượt là trung điểm của \(AC,SC\). Ta có \(DE//SA \Rightarrow DE \bot \left( {ABC} \right)\) mà \(D\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) nên \(ED\) là trục đường trong ngoại tiếp đáy. Do đó: \(EA = EB = EC\) Lại có tam giác \(SAC\) vuông tại \(A\) có \(E\) là trung điểm cạnh huyền nên \(EA = ES = EC = \dfrac{{SC}}{2}\) Suy ra \(EA = ES = EC = EB = \dfrac{{SC}}{2}\) hay \(E\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\) và bán kính mặt cầu là \(\dfrac{{SC}}{2}\) Xét tam giác \(ABC\) vuông tại \(B\) ta có: \(AC = \sqrt {B{C^2} + B{A^2}} = a\sqrt 2 \) Xét tam giác \(SAC\) vuông tại \(A\) ta có: \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {4{a^2} + 2{a^2}} = a\sqrt 6 \) Bán kính mặt cầu cần tìm là: \(R = \dfrac{{SC}}{2} = \dfrac{{a\sqrt 6 }}{2}.\) Chọn D. Câu hỏi 35 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, cạnh \(SA\) vuông góc với đáy, \(SA = a\sqrt 2 \). Biết thể tích khối chóp \(S.ABCD\) bằng \(\dfrac{{\sqrt 2 }}{3}{a^3}\). Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\).
Đáp án: C Phương pháp giải: Tìm tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\) bằng cách : - Tìm tâm \(O\) của đường tròn ngoại tiếp đa giác đáy \(ABCD\). - Dựng đường thẳng \(d\) qua \(O\) và vuông góc với \(\left( {ABCD} \right).\) - \(I\) là giao điểm của \(d\) và mặt phẳng trung trực bất kì của cạnh bên. Tính bán kính của mặt cầu ngoại tiếp hình chóp Lời giải chi tiết:
Gọi \(O = AC \cap BD \Rightarrow O\) là tâm đường tròn ngoại tiếp hình vuông \(ABCD\). Dựng đường thẳng \(d\) qua \(O\) và vuông góc với \(\left( {ABCD} \right).\) Dựng mặt phẳng \(\left( \alpha \right)\) là mặt phẳng trung trực của cạnh bên \(SA\) và cắt \(SA\) tại \(M\). Gọi \(I = d \cap \left( \alpha \right)\) là tâm mặt cầu ngoại tiếp khối chóp \(S.ABCD.\) Ta có : \({V_{S.ABCD}} = \dfrac{1}{3}SA.A{B^2} \Leftrightarrow \dfrac{{\sqrt 2 }}{3}{a^3} = \dfrac{1}{2}.a\sqrt 2 .A{B^2} \Rightarrow AB = a\) \( \Rightarrow AD = a\sqrt 2 \Rightarrow AO = \dfrac{{a\sqrt 2 }}{2}\). Do \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Leftrightarrow MA \bot AO\). Ta có \(SA = a\sqrt 2 \Rightarrow AM = \dfrac{{a\sqrt 2 }}{2} = OI\). Áp dụng định lí Pytago trong tam giác vuông \(OAI\) có: \(R = AI = \sqrt {A{O^2} + O{I^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} = a\). Chọn C. Câu hỏi 36 : Cho điểm \(A\) nằm ngoài mặt cầu \(S\left( {O;R} \right)\). Biết rằng qua \(A\) có vô số tiếp tuyến với mặt cầu. Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu có bán kính bằng \(\dfrac{{\sqrt 2 }}{2}R\). Tính độ dài đoạn thẳng \(OA\) theo \(R.\)
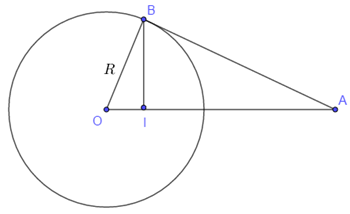
Đáp án: B Phương pháp giải: Vẽ hình và phân tích đề Vận dụng các kiến thức về hình học để tính Lời giải chi tiết:
Giả sử có một tiếp tuyến đi qua \(A\) và cắt mặt cầu tại \(B\). Qua \(B\) kẻ \(BI \bot OA\,\,\,\left( {I \in OA} \right)\) thì \(I\) là tâm đường tròn là tập hợp các tiếp điểm của tiếp tuyến kẻ từ \(A\). Theo giả thiết ta có: \(IB = \dfrac{{\sqrt 2 R}}{2}\). Tam giác \(OBA\) vuông tại \(B\), có chiều cao \(BI\) nên ta có: \(\dfrac{1}{{I{B^2}}} = \dfrac{1}{{O{B^2}}} + \dfrac{1}{{B{A^2}}}\) (hệ thức lượng trong tam giác vuông). \(\begin{array}{l} \Leftrightarrow \dfrac{1}{{{{\left( {\dfrac{{\sqrt 2 R}}{2}} \right)}^2}}} = \dfrac{1}{{{R^2}}} + \dfrac{1}{{B{A^2}}} \Rightarrow BA = R\\ \Rightarrow OA = \sqrt {O{B^2} + B{A^2}} = \sqrt 2 R\end{array}\) Chọn B. Câu hỏi 37 : Cho tứ diện \(ABCD\) có \(AB = AC = AD = 5,\,\,BC = 2;\,\,BD = 3;\,\,CD = 4\). Tính bán kính của mặt cầu ngoại tiếp tứ diện \(ABCD\)?
Đáp án: A Phương pháp giải: - Tìm tâm mặt cầu ngoại tiếp tứ diện \(ABCD\). - Khi đó bán kính của mặt cầu ngoại tiếp của tứ diện \(ABCD\) là \(R = IA = IB = IC = ID\). Lời giải chi tiết:
Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(BCD\), có bán kính là \(r\). Do \(AB = AC = AD = 5\) nên chân đường cao hạ từ \(A\) xuống mặt phẳng \(\left( {BCD} \right)\) trùng với tâm đường tròn ngoại tiếp tam giác \(BCD\) Suy ra \(AO \bot \left( {BCD} \right).\) Gọi \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\) thì \(I\) nằm trên \(AO\). Tam giác \(BCD\) có \(BC = 2;\)\(BD = 3;\)\(CD = 4\) nên \(p = \dfrac{{BC + BD + CD}}{2} = \dfrac{9}{2}\). Khi đó diện tích tam giác \(BCD\)được tính bởi công thức: \({S_{BCD}} = \sqrt {p\left( {p - BC} \right)\left( {p - BD} \right)\left( {p - CD} \right)} = \dfrac{{3\sqrt {15} }}{4}\) Mặt khác, diện tích tam giác \(BCD\) còn tính bởi \({S_{BCD}} = \dfrac{{BC.BD.CD}}{{4r}} \Rightarrow r = \dfrac{{8\sqrt {15} }}{{15}}\) (\(r\) là bán kính đường tròn ngoại tiếp). Suy ra \(OB = OC = OD = \dfrac{{8\sqrt {15} }}{{15}}\). Đặt \(IA = IB = IC = ID = R\), ta có: \(AO \bot \left( {BCD} \right)\) nên \(\begin{array}{l}AO = \sqrt {A{C^2} - O{C^2}} = \sqrt {\dfrac{{311}}{{15}}} \\O{I^2} + O{C^2} = I{C^2}\\ \Leftrightarrow {\left( {OA - IA} \right)^2} + O{C^2} = I{C^2}\\ \Leftrightarrow {\left( {\sqrt {\dfrac{{311}}{{15}}} - R} \right)^2} + {\left( {\dfrac{{8\sqrt {15} }}{{15}}} \right)^2} = {R^2}\\ \Rightarrow R = \dfrac{{25\sqrt {15} }}{{2\sqrt {311} }}\end{array}\) Vậy bán kính mặt cầu ngoại tiếp tứ diện \(ABCD\) bằng \(\dfrac{{25\sqrt {15} }}{{2\sqrt {311} }}\). Chọn A. Câu hỏi 38 : Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, \(AB = 3a,\,\,AD = 4a\), \(SA\) vuông góc với mặt đáy, \(SC\) tạo với mặt phẳng đáy một góc \({60^0}\). Tính bán kính của mặt cầu ngoại tiếp hình chóp \(S.ABCD\) theo \(a\).
Đáp án: B Phương pháp giải: Tìm tâm của mặt cầu ngoại tiếp khối chóp bằng cách : - Tìm tâm \(O\) của đường tròn ngoại tiếp đa giác đáy. - Kẻ đường thẳng \(d\) đi qua tâm \(O\) và vuông góc với mặt phẳng đáy. - Vẽ mặt phẳng \(\left( P \right)\) là mặt phẳng trung trực của một cạnh bên bất kì. - \(I = \left( P \right) \cap d\) là tâm mặt cầu ngoại tiếp khối chóp. Lời giải chi tiết:
Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(I\) là trung điểm cạnh \(SC\). Do \(ABCD\) là hình chữ nhật nên \(O\) là giao điểm 2 đường chéo cũng chình là tâm đường tròn ngoại tiếp hcn \(ABCD\) (do \(OA = OB = OC = OD\)). \(OI\) là đường trung bình trong tam giác \(SAC\) nên \(OI//SA\) mà \(SA\) vuông góc với mp \(\left( {ABCD} \right)\) nên \(OI\) cũng vuông góc với mp \(\left( {ABCD} \right)\) Do đó \(IA = IB = IC = ID\) (do \(I\) nằm trên đường thẳng đi qua tâm \(O\) và vuông góc với đáy). \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \) Tam giác \(SAC\) vuông tại \(A\) có trung tuyến \(AI\) nên \(IA = IS = IC\). \( \Rightarrow IA = IB = IC = ID = IS\) hay \(I\) là tâm mặt cầu ngoại tiếp khối chóp \(S.ABCD\). \(SA\) vuông góc với đáy nên góc tạo bởi \(SC\) và mặt phẳng đáy chính là góc \(\angle SCA \Rightarrow \angle SCA = {60^0}\). \(AC = \sqrt {A{B^2} + B{C^2}} = 5a;\,\,\,SC = \dfrac{{AC}}{{\cos \widehat {SCA}}} = \dfrac{{5a}}{{\cos 60^\circ }} = 10a\). Do đó \(R = IS = \dfrac{1}{2}SC = 5a\). Vậy bán kính mặt cầu ngoại tiếp khối chóp bằng \(5a\). Chọn B. Câu hỏi 39 : Cho hình chóp O.ABC có \(OA = OB = OC = a,\)\(\angle AOB = {60^0},\)\(\angle BOC = {90^0},\)\(\angle AOC = {120^0}\). Gọi \(S\) là trung điểm cạnh \(OB\). Bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\) là:
Đáp án: D Phương pháp giải: Sử dụng tính chất của tam giác đồng dạng Lời giải chi tiết:
Tam giác \(OAB\) có \(\left\{ \begin{array}{l}OA = OB\,\,\left( {gt} \right)\\\angle AOB = {60^0}\,\,\left( {gt} \right)\end{array} \right. \Rightarrow \Delta OAB\) đều \( \Rightarrow AB = a\). Tam giác \(OBC\) có \(\left\{ \begin{array}{l}OB = OC\,\,\left( {gt} \right)\\\angle BOC = {90^0}\,\,\left( {gt} \right)\end{array} \right. \Rightarrow \Delta OBC\) vuông cân tại \(O\) \( \Rightarrow BC = a\sqrt 2 \). Tam giác \(OAC\) có \(\left\{ \begin{array}{l}OA = OC\,\,\left( {gt} \right)\\\angle AOC = {120^0}\end{array} \right.\), áp dụng định lí Cosin trong tam giác ta có \(AC = \sqrt {O{A^2} + O{C^2} - 2OA.OC.\cos \angle AOC} = a\sqrt 3 \). Khi đó ta có \(A{C^2} = A{B^2} + A{C^2}\), do đó tam giác \(ABC\) vuông tại \(B\) (định lí Pytago đảo). Gọi \(H\) là trung điểm của \(AC\), suy ra \(H\) là tâm đường tròn ngoại tiếp \(\Delta ABC\). Chóp \(O.ABC\) có các cạnh bên bằng nhau, do đó chân đường cao trùng với tâm đường tròn ngoại tiếp đáy nên \(OH \bot \left( {ABC} \right)\), suy ra \(OH \bot HB\) \( \Rightarrow \Delta OBH\) vuông tại \(H\). Gọi \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\), \(J\) là trung điểm của \(SB\). Vì \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\) nên \(IS = IA = IB = IC\) \( \Rightarrow IS = IB\) và \(I \in OH\). \( \Rightarrow \Delta ISB\) cân tại \(I\), do đường trùng tuyến \(IJ\) đồng thời là đường cao \( \Rightarrow IJ \bot SB\). Xét \(\Delta OIJ\) và \(\Delta OBH\) có: \(\angle BOH \) chung; \(\angle SJI = \angle SHB = {90^0}\). \( \Rightarrow \Delta OIJ \sim \Delta OBH\,\,\left( {g.g} \right)\) \( \Rightarrow \dfrac{{OJ}}{{OH}} = \dfrac{{IJ}}{{HB}} \Rightarrow IJ = \dfrac{{OJ.HB}}{{OH}}\). Ta có: \(OJ = \dfrac{3}{4}OB = \dfrac{3}{4}a\). Tam giác \(ABC\) vuông tại \(B\) nên \(HB = \dfrac{1}{2}AC = \dfrac{{a\sqrt 3 }}{2}\). Áp dụng định lí Pytago trong tam giác vuông có: \(OH = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}} = \dfrac{a}{2}\). \(\begin{array}{l} \Rightarrow IJ = \dfrac{{\dfrac{{3a}}{4}.\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{a}{2}}} = \dfrac{{3a\sqrt 3 }}{4}\\ \Rightarrow R = SI = \sqrt {S{J^2} + I{J^2}} = \sqrt {{{\left( {\dfrac{a}{4}} \right)}^2} + {{\left( {\dfrac{{3a\sqrt 3 }}{4}} \right)}^2}} = \dfrac{{a\sqrt 7 }}{2}.\end{array}\) Chọn D. Câu hỏi 40 : Cho tứ diện \(ABCD\) có \(BC = a,\) \(CD = a\sqrt 3 ,\) \(\widehat {BCD} = \widehat {ABC} = \widehat {ADC} = {90^0}\). Số đo góc giữa hai đường thẳng \(BC\) và \(AD\) bằng \({60^0}\). Bán kính mặt cầu ngoại tiếp tứ diện \(ABCD\) bằng:
Đáp án: D Phương pháp giải: Tam giác ABC vuông tại A suy ra A, B, C nằm trên mặt cầu đường kính BC. Lời giải chi tiết:
Gọi I, O, M lần lượt là trung điểm của AC, BD, CD. Do \(\widehat {ABC} = \widehat {ADC} = {90^0}\) nên A, B, C, D nằm trên mặt cầu (S) tâm I, đường kính AC. Lại có, tam giác BCD vuông tại C \( \Rightarrow \) O là tâm đường tròn (C) ngoại tiếp tam giác BCD (trên mặt phẳng (BCD) \( \Rightarrow OI \bot \left( {BCD} \right)\) Ta có: \(OM//BC,\,\,IM//CD,\,\) góc giữa hai đường thẳng \(BC\) và \(AD\) bằng \({60^0} \Rightarrow \left( {\widehat {IM;OM}} \right) = {60^0}\) \( \Rightarrow \Delta OIM\) vuông tại O và \(\widehat {IMO} = {60^0}\). Ta có: \(BD = \sqrt {B{C^2} + C{D^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}} = 2a \Rightarrow r = a\) (bán kính đường tròn (C) Khoảng cách từ tâm I đến (BCD): \(d = OI = OM.\tan \widehat {IMO} = \dfrac{1}{2}.a.\tan {60^0} = \dfrac{{a\sqrt 3 }}{2}\) Ta có: \({R^2} = {r^2} + {d^2} = {a^2} + {\left( {\dfrac{{a\sqrt 3 }}{2}} \right)^2} = \dfrac{{7{{\rm{a}}^2}}}{4} \Leftrightarrow R = \dfrac{{a\sqrt 7 }}{2}\) (R là bán kính mặt cầu (S)). Chọn D.
|