Phương pháp giải:

Hàm số: \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0.\)

Lời giải chi tiết:

+) Xét đáp án A: \(y =  - 2 + 3x\) có \(a = 3 > 0 \Rightarrow \) hàm số đồng biến trên \(\mathbb{R}.\)

Đáp án A.

Phương pháp giải:

\(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\).

\(\frac{1}{A}\) xác định \( \Leftrightarrow A \ne 0\).

Lời giải chi tiết:

Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\x - 3 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \ne 3\end{array} \right.\).

Vậy tập xác định của hàm số là \(D = \left( { - 2; + \infty } \right]\backslash \left\{ 3 \right\}\).

Đáp án D.

Phương pháp giải:

Cho hàm số y = f(x) có tập xác định là D.

- Nếu \(\forall x \in D \Rightarrow  - x \in D\) và f(-x) = f(x) thì hàm số là hàm số chẵn.

- Nếu \(\forall x \in D \Rightarrow  - x \in D\) và f(-x) = –f(x) thì hàm số là hàm số chẵn.

Lời giải chi tiết:

Xét đáp án D ta có:

TXĐ: D = R nên \(\forall x \in D \Rightarrow  - x \in D\).

Đặt \(y = f\left( x \right) =  - {x^4} + 3{x^2} + 1\) ta có:

\(\begin{array}{l}f\left( { - x} \right) =  - {\left( { - x} \right)^4} + 3{\left( { - x} \right)^2} + 1\\f\left( { - x} \right) =  - {x^4} + 3{x^2} + 1\\f\left( { - x} \right) = f\left( x \right)\end{array}\)

Vậy hàm số \(y =  - {x^4} + 3{x^2} + 1\) là hàm số chẵn.

Đáp án D.

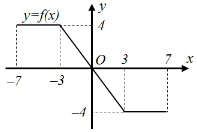
Phương pháp giải:

Thay các giá trị x = 5 và x =  – 5  vào hàm số f (x) tương ứng rồi tính giá trị biểu thức.

Lời giải chi tiết:

Ta có:\(\left\{ \begin{array}{l}f\left( 5 \right) = \frac{{\sqrt {5 + 4}  - 1}}{{5 - 1}} = \frac{1}{2}\\f\left( { - 5} \right) = 3 - \left( { - 5} \right) = 8\end{array} \right.\) \( \Rightarrow f\left( 5 \right) + f\left( { - 5} \right) = \frac{1}{2} + 8 = \frac{{17}}{2}.\)

Đáp án  C.

Phương pháp giải:

Dựa vào đồ thị hàm số nhận xét các khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết:

Khẳng định A sai vì hàm số là hàm hằng trên các đoạn \(\left[ { - 7; - 3} \right]\) và \(\left[ {3;7} \right].\)

Chọn A.

Phương pháp giải:

Tìm tập xác định của hàm số.

Lời giải chi tiết:

Xét hàm số \(y = \frac{x}{{{x^2} + 1}}\) có điều kiện xác định là \({x^2} + 1 \ne 0,\) luôn đúng nên hàm số có tập xác định là \(\mathbb{R}.\)

Chọn B.

Phương pháp giải:

Biểu thức \(\sqrt {f\left( x \right)} \) xác định nếu \(f\left( x \right) \ge 0\).

Lời giải chi tiết:

ĐK: \(1 - x \ge 0 \Leftrightarrow x \le 1\).

TXĐ: \(D = \left( { - \infty ;1} \right]\).

Chọn A.

Phương pháp giải:

Hàm số \(f\left( x \right)\) xác định trên tập đối xứng \(D\) là hàm chẵn nếu \(f\left( { - x} \right) = f\left( x \right)\).

Lời giải chi tiết:

Đáp án A: TXĐ: \(D = \mathbb{R}\).

Ta thấy \(f\left( { - x} \right) =  - \left( { - x} \right) = x =  - f\left( x \right)\) nên hàm số lẻ.

Đáp án B: TXĐ: \(D = \mathbb{R}\).

Có \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\) nên hàm số chẵn.

Chọn B.

Phương pháp giải:

Biểu thức \(\frac{1}{{f\left( x \right)}}\) xác định khi \(f\left( x \right) \ne 0\).

Lời giải chi tiết:

ĐK: \({x^2} + 4 \ne 0\).

Do \({x^2} + 4 > 0,\forall x \in \mathbb{R}\) nên TXĐ: \(D = \mathbb{R}\).

Chọn B.

Phương pháp giải:

Biểu thức \(\sqrt {f\left( x \right)} \) xác định nếu \(f\left( x \right) \ge 0\).

Biểu thức \(\frac{1}{{f\left( x \right)}}\) xác định nếu \(f\left( x \right) \ne 0\).

Lời giải chi tiết:

ĐK: \(\left\{ \begin{array}{l}x - 1 \ge 0\\x + 4 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \ne  - 4\end{array} \right. \Leftrightarrow x \ge 1\).

Tập xác định \(D = \left[ {1; + \infty } \right)\).

Chọn D.

Phương pháp giải:

Biểu thức \(\frac{1}{{f\left( x \right)}}\) xác định \( \Leftrightarrow f\left( x \right) \ne 0,\) biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\)

Lời giải chi tiết:

Hàm số \(f\left( x \right) = \frac{{\sqrt {2 - x}  + \sqrt {2 + x} }}{x}\) xác định

\( \Leftrightarrow \left\{ \begin{array}{l}2 - x \ge 0\\2 + x \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\x \ge  - 2\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2 \le x \le 2\\x \ne 0\end{array} \right..\)

Vậy hàm số \(f\left( x \right) = \frac{{\sqrt {2 - x}  + \sqrt {2 + x} }}{x}\) có tập xác định là \(D = \left[ { - 2;2} \right]\backslash \left\{ 0 \right\}.\)

Chọn A.

Phương pháp giải:

Xét hàm số \(y = f\left( x \right)\) có tập xác định \(D\)

Với \(\forall \,\,x \in D \Rightarrow  - x \in D\) ta có:

\( + )\,\,\,f\left( { - x} \right) = f\left( x \right) \Rightarrow f\left( x \right)\) là hàm số chẵn.

\( + )\,\,\,f\left( { - x} \right) =  - f\left( x \right) \Rightarrow f\left( x \right)\) là hàm số lẻ.

Lời giải chi tiết:

Xét hàm số \(f\left( x \right) = \sqrt {3 + x}  - \sqrt {3 - x} \) có tập xác định là \(D = \left[ { - 3;3} \right]\).

\( \Rightarrow \forall x \in D\) thì \( - x \in D.\)

Có \(f\left( { - x} \right) = \sqrt {3 + \left( { - x} \right)}  - \sqrt {3 - \left( { - x} \right)}  =  - \left( {\sqrt {3 + x}  - \sqrt {3 - x} } \right).\)

Vậy \(f\left( x \right) =  - f\left( { - x} \right)\) nên đây là hàm số lẻ.

Chọn C.

Phương pháp giải:

Phương pháp đánh giá.

Lời giải chi tiết:

Ta có \(f\left( x \right) = \left| { - 5x} \right| \ge 0,\forall x\) nên khẳng định D sai.

Chọn D.

Phương pháp giải:

Xét tính chẵn, lẻ của hàm số đã cho.

+) Hàm số là hàm chẵn thì hàm số có trục \(Oy\) là trục đối xứng.

+) Hàm số là hàm lẻ thì hàm số có tâm \(O\) là tâm đối xứng.

Lời giải chi tiết:

Ta có: \(f\left( x \right) = \left| {x + 2018} \right| + \left| {x - 2018} \right|\)

TXĐ: \(D = \mathbb{R} \Rightarrow \) đáp án D đúng.

Với mọi \(x \in \mathbb{R} \Rightarrow  - x \in \mathbb{R}.\) Khi đó ta có:

\(f\left( { - x} \right) = \left| { - x + 2018} \right| + \left| { - x - 2018} \right| = \left| {x - 2018} \right| + \left| {x + 2018} \right| = f\left( x \right)\)

\( \Rightarrow \) Hàm số là hàm số chẵn và nhận trục \(Oy\) làm trục đối xứng.

\( \Rightarrow \) đáp án B và C đúng.

Chọn A.

Phương pháp giải:

Hàm số \(f\left( x \right)\) là hàm số chẵn nếu với mọi \(x \in D\), ta có \( - x \in D\) và \(f\left( { - x} \right) = f\left( x \right).\) 

Hàm số \(f\left( x \right)\) là hàm số lẻ nếu với mọi \(x \in D\), ta có  và \(f\left( { - x} \right) =  - f\left( x \right).\) 

Lời giải chi tiết:

Ta có:

1) \(f\left( { - x} \right) = \frac{{{{\left( { - x} \right)}^4} + 10}}{{\left( { - x} \right)}} =  - \frac{{{x^4} + 10}}{x} =  - f\left( x \right)\,\, \Rightarrow \) hàm số là hàm lẻ.

2) \(f\left( { - x} \right) = \frac{1}{{20 - {{\left( { - x} \right)}^2}}} = \frac{1}{{20 - {x^2}}} = f\left( x \right) \Rightarrow \) hàm số là hàm chẵn.

3) \(f\left( { - x} \right) =  - 7{\left( { - x} \right)^4} + 2\left| { - x} \right| + 1 =  - 7{x^4} + 2\left| x \right| + 1 = f\left( { - x} \right) \Rightarrow \) hàm số là hàm chẵn.

4) \(f\left( { - x} \right) = \left| { - x + 2} \right| - \left| { - x - 2} \right| = \left| {x - 2} \right| - \left| {x + 2} \right| =  - f\left( x \right)\,\, \Rightarrow \) hàm số là hàm lẻ.

Vậy có hai hàm số chẵn.

Chọn A.

Phương pháp giải:

Biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0,\) biểu thức \(\frac{1}{{g\left( x \right)}}\) xác định \( \Leftrightarrow g\left( x \right) \ne 0.\)

Lời giải chi tiết:

Ta có: \(\left\{ \begin{array}{l}2x - 6 \ge 0\\x - 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x \ne 3\end{array} \right. \Rightarrow x > 3 \Rightarrow D = \left( {3; + \infty } \right).\)

Chọn B.

Phương pháp giải:

Hàm số \(f\left( x \right)\) là hàm số chẵn nếu với mọi \(x \in D\), ta có \( - x \in D\) và \(f\left( { - x} \right) = f\left( x \right)\) 

Hàm số \(f\left( x \right)\)  là hàm số lẻ nếu với mọi \(x \in D\), ta có \( - x \in D\) và \(f\left( { - x} \right) =  - f\left( x \right)\) 

Lời giải chi tiết:

\(f\left( { - x} \right) = \frac{{\sqrt {1 + \left( { - x} \right)}  + \sqrt {1 - \left( { - x} \right)} }}{{\left( { - x} \right)}} =  - \frac{{\sqrt {1 - x}  + \sqrt {1 + x} }}{x} =  - f\left( x \right)\,\, \Rightarrow \) hàm số là hàm lẻ.

\(g\left( { - x} \right) = \left| { - {x^3}} \right| - 4\left| { - x} \right| = \left| {{x^3}} \right| - 4\left| x \right| = g\left( x \right)\, \Rightarrow \) hàm số là hàm chẵn.

Chọn D.

Phương pháp giải:

Biểu thức: \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\)

Lời giải chi tiết:

Điều kiện: \(\left\{ \begin{array}{l}x - 1 \ge 0\\2x - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \ge \frac{1}{2}\end{array} \right. \Rightarrow x \ge 1 \Rightarrow D = \left[ {1; + \infty } \right).\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

Tập xác định: \(D = \left[ { - \frac{1}{2};\frac{1}{2}} \right]\)

Với mọi \(x \in D \Rightarrow - x \in D\) và

\(f\left( { - x} \right) = \sqrt {1 - 2\left( { - x} \right)}  - \sqrt {1 + 2\left( { - x} \right)}  = \sqrt {1 + 2x}  - \sqrt {1 - 2x}  =  - f\left( x \right)\)

Vậy hàm số đã cho là hàm số lẻ.

Phương pháp giải:

Lời giải chi tiết:

Tập xác định : \(D = R\backslash \left\{ { - 1;\,\,1} \right\}.\)

Với mọi \(  x \in D\) thì \( - x \in D\) và

\(f\left( { - x} \right) = \frac{{ - x}}{{\left( { - x - 1} \right)\left( { - x + 1} \right)}} = \frac{{ - x}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} =  - f\left( x \right)\)

Vậy hàm số đã cho là hàm số lẻ.

Phương pháp giải:

Lời giải chi tiết:

Tập xác định: \(D = R\backslash \left\{ 0 \right\}.\)

Với mọi \(x \in D \Rightarrow  - x \in D\) và

\(f\left( { - x} \right) = \frac{{\left| { - x - 1} \right| - \left| { - x + 1} \right|}}{{\left| { - x + 2} \right| - \left| { - x - 2} \right|}} = \frac{{\left| {x - 1} \right| - \left| {x + 1} \right|}}{{\left| {x + 2} \right| - \left| {x - 2} \right|}} = f\left( x \right).\)

Vậy hàm số đã cho là hàm số chẵn.

Phương pháp giải:

Lời giải chi tiết:

Hàm số xác định \(\Leftrightarrow \) \(\sqrt {{x^2} - 2x + 2}  \ne \sqrt {{x^2} + 2x + 2}  \Leftrightarrow x \ne 0\).

Tập xác định: \(D = R\backslash \left\{ 0 \right\}.\)

Với mọi \(x \in D\) thì \( - x \in D\) và

\(f\left( { - x} \right) = \frac{1}{{\sqrt {{x^2} + 2x + 2}  - \sqrt {{x^2} - 2x + 2} }} = \frac{{ - 1}}{{\sqrt {{x^2} - 2x + 2}  - \sqrt {{x^2} + 2x + 2} }} =  - f\left( x \right)\).

Vậy hàm số đã cho là hàm số lẻ.

Phương pháp giải:

\(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\).

Lời giải chi tiết:

Hàm số xác định

\( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {m^2} \ge 0\,\,\left( {luon\,\,dung} \right)\\{x^2} - m \ge 0\end{array} \right. \Leftrightarrow {x^2} \ge m\).

Để hàm số xác định trên R thì \({x^2} \ge m\,\,\forall x \in R\).

Mà \({x^2} \ge 0\,\,\forall x \Rightarrow m \le 0\).

Vậy \(m \in \left( { - \infty ;0} \right]\).

Đáp án D.

Phương pháp giải:

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) =  - f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số lẻ và có đồ thị hàm số đối xứng qua gốc tọa độ \(O.\)

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) = f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số chẵn và có đồ thị hàm số đối xứng qua trục tung \(Oy.\)

Lời giải chi tiết:

Ta có TXĐ: \(D = \mathbb{R} \Rightarrow \forall x \in D \Rightarrow  - x \in D\)

Đồ thị hàm số đã cho nhận trục tung làm trục đối xứng \( \Leftrightarrow \) hàm số đã cho là hàm số chẵn

\(\begin{array}{l} \Leftrightarrow f\left( { - x} \right) = f\left( x \right),\forall x \in \mathbb{R}\\ \Leftrightarrow {\left( { - x} \right)^4} - \left( {{m^2} - 3m + 2} \right){\left( { - x} \right)^3} + {m^2} - 1 = {x^4} - \left( {{m^2} - 3m + 2} \right){x^3} + {m^2} - 1,\forall x \in \mathbb{R}\\ \Leftrightarrow {x^4} + \left( {{m^2} - 3m + 2} \right){x^3} + {m^2} - 1 = {x^4} - \left( {{m^2} - 3m + 2} \right){x^3} + {m^2} - 1,\forall x \in \mathbb{R}\\ \Leftrightarrow 2\left( {{m^2} - 3m + 2} \right){x^3} = 0,\,\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow {m^2} - 3m + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 1}\\{m = 2}\end{array}} \right.\end{array}\)

Vậy có 2 giá trị của \(m\) thỏa mãn bài toán.

Chọn  A

Phương pháp giải:

Hàm số \(\frac{1}{{f\left( x \right)}}\) xác định \( \Leftrightarrow f\left( x \right) \ne 0.\)

Lời giải chi tiết:

Hàm số \(y = \frac{{2x + 1}}{{{x^2} - 2x + m - 2}}\) xác định trên \(\mathbb{R}\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 2x + m - 2 \ne 0{\rm{ }}\forall x \in \mathbb{R}\\ \Leftrightarrow {\left( {x - 1} \right)^2} + m - 3 \ne 0{\rm{ }}\forall x \in \mathbb{R}\\ \Leftrightarrow {\left( {x - 1} \right)^2} \ne  - \left( {m - 3} \right)\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow  - \left( {m - 3} \right) < 0\\ \Leftrightarrow m - 3 > 0\\ \Leftrightarrow m > 3\end{array}\) 

Chọn  A.

Phương pháp giải:

Hàm số \(f\left( x \right) = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0.\)

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\)

Hàm số \(f\left( x \right) = \left( {m + 1} \right)x + m - 2\) đồng biến trên \(\mathbb{R} \Leftrightarrow m + 1 > 0 \Leftrightarrow m >  - 1.\)

Lại có: \(\left\{ \begin{array}{l}m \in \mathbb{Z}\\m \in \left[ { - 3;\,\,3} \right]\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m \in \mathbb{Z}\\ - 1 < m \le 3\end{array} \right. \Rightarrow m \in \left\{ {0;\,\,1;\,\,2;\,\,3} \right\}.\)

Vậy có 4 giá trị nguyên của \(m\)  thoả mãn bài toán.

Chọn  C.

Phương pháp giải:

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) =  - f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số lẻ và có đồ thị hàm số đối xứng qua gốc tọa độ \(O.\)

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) = f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số chẵn và có đồ thị hàm số đối xứng qua trục tung \(Oy.\)

Lời giải chi tiết:

Ta có \(\sqrt {{x^2} + 1}  > \sqrt {{x^2}}  = \left| x \right| \ge x \Rightarrow \sqrt {{x^2} + 1}  - x \ne 0\) với mọi \(x\).

Suy ra TXĐ: \(D = \mathbb{R}\)

Mặt khác  \(\sqrt {{x^2} + 1}  > \sqrt {{x^2}}  = \left| x \right| \ge  - x \Rightarrow \sqrt {{x^2} + 1}  + x \ne 0\) do đó

\(f(x) = \frac{{{{\left( {x + \sqrt {{x^2} + 1} } \right)}^2}}}{{\left( {\sqrt {{x^2} + 1}  + x} \right)\left( {\sqrt {{x^2} + 1}  - x} \right)}} - 2{x^2} - 1 = \frac{{{x^2} + 2x\sqrt {{x^2} + 1}  + {x^2} + 1}}{{{x^2} + 1 - {x^2}}} - 2{x^2} - 1 = 2x\sqrt {{x^2} + 1} \)

Với mọi \(x \in \mathbb{R}\) ta có \( - x \in \mathbb{R}\)  và \(f\left( { - x} \right) = 2\left( { - x} \right)\sqrt {{{\left( { - x} \right)}^2} + 1}  =  - 2x\sqrt {{x^2} + 1}  =  - f\left( x \right)\)

Do đó \(f\left( x \right) = \frac{{x + \sqrt {{x^2} + 1} }}{{\sqrt {{x^2} + 1}  - x}} - 2{x^2} - 1\) là hàm số lẻ.

Chọn A.

Phương pháp giải:

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) =  - f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số lẻ và có đồ thị hàm số đối xứng qua gốc tọa độ \(O.\)

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) = f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số chẵn và có đồ thị hàm số đối xứng qua trục tung \(Oy.\)

Lời giải chi tiết:

Ta có TXĐ: \(D = \mathbb{R} \Rightarrow \forall x \in D \Rightarrow  - x \in D\)

Đồ thị hàm số đã cho nhận gốc tọa độ \(O\)  làm tâm đối xứng \( \Leftrightarrow \) hàm số đã cho là hàm số lẻ

\(\begin{array}{l} \Leftrightarrow f\left( { - x} \right) =  - f\left( x \right),\forall x \in \mathbb{R}\\ \Leftrightarrow {\left( { - x} \right)^3} - \left( {{m^2} - 9} \right){\left( { - x} \right)^2} + \left( {m + 3} \right)\left( { - x} \right) + m - 3 =  - \left[ {{x^3} - \left( {{m^2} - 9} \right){x^2} + \left( {m + 3} \right)x + m - 3} \right],\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow  - {x^3} - \left( {{m^2} - 9} \right){x^2} - \left( {m + 3} \right)x + m - 3 =  - {x^3} + \left( {{m^2} - 9} \right){x^2} - \left( {m + 3} \right)x - m + 3,\,\,\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow 2\left( {{m^2} - 9} \right){x^2} - 2\left( {m - 3} \right) = 0,\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{m^2} - 9 = 0}\\{m - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 3\\m =  - 3\end{array} \right.\\m = 3\end{array} \right. \Leftrightarrow m = 3\end{array}\)

Chọn  B

Phương pháp giải:

 \(\begin{array}{l}y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{f_1}\left( x \right){\rm{ }}\,\,khi\,\,\,\,\,x \in {D_1}{\rm{ }}}\\{{f_2}\left( x \right)\,\,\,{\rm{ }}khi\,\,\,x \in {D_2}}\\{{f_3}\left( x \right){\rm{ }}\,khi\,\,\,x \in {D_3}}\end{array}} \right.\\{D_f} = {D_1} \cup {D_2} \cup {D_3}\\f\left( {{x_1}} \right) = {f_1}\left( {{x_1}} \right){\rm{ }};{\rm{ }}{x_1} \in {D_1}\\f\left( {{x_2}} \right) = {f_2}\left( {{x_2}} \right){\rm{ ; }}{x_2} \in {D_2}\\f\left( {{x_3}} \right) = {f_3}\left( {{x_3}} \right){\rm{ ; }}{x_3} \in {D_3}\end{array}\)

\({x_4} \notin D \Rightarrow \) không tồn tại \(f\left( {{x_4}} \right).\)

Lời giải chi tiết:

Ta có: \(\left\{ \begin{array}{l}f\left( 2 \right) = \frac{{2\sqrt {2 + 2}  - 3}}{{2 - 1}} = 1\\f\left( { - 2} \right) = {\left( { - 2} \right)^2} + 1 = 5\end{array} \right. \Rightarrow P = 1 + 5 = 6.\)  

Chọn  C.

Phương pháp giải:

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) =  - f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số lẻ và có đồ thị hàm số đối xứng qua gốc tọa độ \(O.\)

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) = f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số chẵn và có đồ thị hàm số đối xứng qua trục tung \(Oy.\)

Lời giải chi tiết:

\(\begin{array}{l} + )\,\,\,f\left( x \right) = {x^{2018}} - 2017\\D = \mathbb{R}\\\forall x \in D \Rightarrow  - x \in D\\f( - x) = {\left( { - x} \right)^{2018}} - 2017 = {x^{2018}} - 2017 = f\left( x \right)\end{array}\) 

\( \Rightarrow \) Hàm số trên là hàm số chẵn \( \Rightarrow \) loại đáp án A.

\(\begin{array}{l} + )\,\,f(x) = \sqrt {2x + 3} \\D = \left[ { - \frac{3}{2};\,\, + \infty } \right).\end{array}\)

Vì \(D\) là tập không đối xứng nên hàm số không chẵn, không lẻ \( \Rightarrow \) loại đáp án B.

\(\begin{array}{l} + )\,\,\,f\left( x \right) = \sqrt {3 + x}  - \sqrt {3 - x} \\D = \left[ { - 3;3} \right]\\\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) = \sqrt {3 + \left( { - x} \right)}  - \sqrt {3 - \left( { - x} \right)}  = \sqrt {3 - x}  - \sqrt {3 + x}  =  - f\left( x \right)\end{array}\)

\( \Rightarrow \) Hàm số trên là hàm lẻ \( \Rightarrow \) đáp án C đúng.

\(\begin{array}{l} + )\,\,\,f\left( x \right) = \left| {x + 3} \right| + \left| {x - 3} \right|\\D = \mathbb{R}\\\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) = \left| { - x + 3} \right| + \left| { - x - 3} \right| = \left| {x - 3} \right| + \left| {x + 3} \right| = f\left( x \right)\end{array}\)

\( \Rightarrow \) Hàm số trên là hàm chẵn \( \Rightarrow \) loại đáp án D.

Chọn  C.

Phương pháp giải:

Hàm số \(y = \frac{1}{{f\left( x \right)}}\)  xác định \( \Leftrightarrow f\left( x \right) \ne 0.\)

Lời giải chi tiết:

Hàm số đã cho có nghĩa

\(\begin{array}{l} \Leftrightarrow \left( {\sqrt[3]{{{x^2} - 3x + 2}} - \sqrt[3]{{{x^2} - 7}}} \right) \ne 0\\ \Leftrightarrow \sqrt[3]{{{x^2} - 3x + 2}}{\rm{ }} \ne {\rm{ }}\sqrt[3]{{{x^2} - 7}}\\ \Leftrightarrow {x^2} - 3x + 2{\rm{ }} \ne {\rm{ }}{x^2} - 7\\ \Leftrightarrow  - 3x \ne  - 9\\ \Leftrightarrow x \ne 3\end{array}\)

Vậy TXĐ: \(D = \mathbb{R}\backslash \left\{ 3 \right\}.\)

Chọn  A.

Phương pháp giải:

 \(\begin{array}{l}y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{f_1}\left( x \right){\rm{ }}\,\,khi\,\,\,\,\,x \in {D_1}{\rm{ }}}\\{{f_2}\left( x \right)\,\,\,{\rm{ }}khi\,\,\,x \in {D_2}}\\{{f_3}\left( x \right){\rm{ }}\,khi\,\,\,x \in {D_3}}\end{array}} \right.\\{D_f} = {D_1} \cup {D_2} \cup {D_3}\\f\left( {{x_1}} \right) = {f_1}\left( {{x_1}} \right){\rm{ }};{\rm{ }}{x_1} \in {D_1}\\f\left( {{x_2}} \right) = {f_2}\left( {{x_2}} \right){\rm{ ; }}{x_2} \in {D_2}\\f\left( {{x_3}} \right) = {f_3}\left( {{x_3}} \right){\rm{ ; }}{x_3} \in {D_3}\end{array}\)

\({x_4} \notin D \Rightarrow \) không tồn tại \(f\left( {{x_4}} \right).\)

Lời giải chi tiết:

Vì \(4 \in \left( {2;5} \right]\) nên \(f\left( 4 \right) = {4^2} - 1 = 16 - 1 = 15.\)

Chọn  B.

Phương pháp giải:

Hàm số \({\rm{y  = }}ax + b\left( {a \ne 0} \right)\). Khi đó:

Hàm số đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0.\)

Hàm số nghịch biến trên \(\mathbb{R} \Leftrightarrow a < 0.\)

Lời giải chi tiết:

Hàm số \(y = 4 - 3x\) có \(a =  - 3 < 0\) nên hàm số đã cho nghịch biến trên \(\mathbb{R}.\) 

Chọn  C.

Phương pháp giải:

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) = f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số chẵn và đồ thị đối xứng qua \(Oy.\)

Lời giải chi tiết:

\(D = \mathbb{R}\)

Ta có: \(f\left( x \right) = {x^2} - \left| x \right|\)

Với \(x \in D \Rightarrow  - x \in D\) ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} - \left| { - x} \right| = {x^2} - \left| x \right| = f\left( x \right).\)

\( \Rightarrow f\left( x \right) = {x^2} - \left| x \right|\) là hàm số chẵn và đồ thị đối xứng qua \(Oy.\)

Chọn  B.

Phương pháp giải:

\(y = \frac{1}{{f\left( x \right)}}\) có nghĩa \( \Leftrightarrow f\left( x \right) \ne 0.\)

Lời giải chi tiết:

Hàm số đã cho xác định \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x + 1 \ne 0}\\{x - 3 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne \frac{{ - 1}}{2}}\\{x \ne 3}\end{array}} \right.} \right.\)

Vậy TXĐ là: \(D = \mathbb{R}\backslash \left\{ {\frac{{ - 1}}{2};3} \right\}.\)

Chọn  B.

Phương pháp giải:

\(\left. \begin{array}{l}\forall x \in D \Rightarrow  - x \in D\\f\left( { - x} \right) = f\left( x \right)\end{array} \right\} \Rightarrow f\left( x \right)\) là hàm số chẵn và có đồ thị hàm số đối xứng qua trục tung \(Oy.\)

Lời giải chi tiết:

ĐKXĐ: \(\sqrt {{x^2} + 1}  \ne m\,\,\,\left( * \right)\) (*)

Hàm số đã cho là hàm số chẵn \( \Leftrightarrow f\left( { - x} \right) = f\left( x \right)\)  với mọi \(x\) thỏa mãn điều kiện \(\left( * \right)\)

\( \Leftrightarrow \frac{{{x^2}\left( {{x^2} - 2} \right) - \left( {2{m^2} - 2} \right)x}}{{\sqrt {{x^2} + 1}  - m}} = \frac{{{x^2}\left( {{x^2} - 2} \right) + \left( {2{m^2} - 2} \right)x}}{{\sqrt {{x^2} + 1}  - m}}\) với mọi \(x\)  thỏa mãn điều kiện \(\left( * \right)\)

\( \Leftrightarrow {x^2}\left( {{x^2} - 2} \right) - \left( {2{m^2} - 2} \right)x = {x^2}\left( {{x^2} - 2} \right) + \left( {2{m^2} - 2} \right)x\) với mọi \(x\) thỏa mãn điều kiện (*)

\( \Leftrightarrow 2\left( {2{m^2} - 2} \right)x = 0\) với mọi \(x\) thỏa mãn điều kiện (*)

\( \Leftrightarrow 2{m^2} - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m =  - 1\end{array} \right.\)

*  Với \(m = 1\) ta có hàm số là \(f\left( x \right) = \frac{{{x^2}\left( {{x^2} - 2} \right)}}{{\sqrt {{x^2} + 1}  - 1}}\)

ĐKXĐ : \(\sqrt {{x^2} + 1}  \ne 1 \Leftrightarrow x \ne 0\)

Suy ra TXĐ: \({\rm{D}} = \mathbb{R}\backslash \left\{ 0 \right\}\)

Dễ thấy với mọi \(x \in \mathbb{R}\backslash \left\{ 0 \right\}\) ta có \( - x \in \mathbb{R}\backslash \left\{ 0 \right\}\) và \(f\left( { - x} \right) = f\left( x \right)\)

Do đó \(f\left( x \right) = \frac{{{x^2}\left( {{x^2} - 2} \right)}}{{\sqrt {{x^2} + 1}  - 1}}\) là hàm số chẵn.

*  Với \(m =  - 1\)  ta có hàm số là \(f\left( x \right) = \frac{{{x^2}\left( {{x^2} - 2} \right)}}{{\sqrt {{x^2} + 1}  + 1}}\)

TXĐ: \({\rm{D}} = \mathbb{R}\)

Dễ thấy với mọi \(x \in \mathbb{R}\) ta có \( - x \in \mathbb{R}\) và \(f\left( { - x} \right) = f\left( x \right)\)

Do đó \(f\left( x \right) = \frac{{{x^2}\left( {{x^2} - 2} \right)}}{{\sqrt {{x^2} + 1}  + 1}}\) là hàm số chẵn.

Vậy \(m =  \pm 1\) là giá trị cần tìm.

Chọn  D.

Phương pháp giải:

Điểm \(A({x_0};{y_0})\) thuộc vào đồ thị hàm số \(y = f\left( x \right)\) nếu \({y_0} = f\left( {{x_0}} \right).\)

Lời giải chi tiết:

Thay lần lượt toạ độ của các điểm \({M_1},\,{M_2},{M_3},{M_4}\) vào hàm số \(y = \frac{1}{{x - 1}},\) ta có:

\({M_1}\left( {2;1} \right)\): \(1 = \frac{1}{{2 - 1}} \Leftrightarrow 1 = 1\) (luôn đúng)

\({M_2}\left( {1;1} \right):1 = \frac{1}{{1 - 1}} \Leftrightarrow 1 = \frac{1}{0}\) (vô lý)

\({M_3}\left( {2;0} \right):0 = \frac{1}{{2 - 1}} \Leftrightarrow 0 = 1\) (vô lý)

\({M_4}\left( {0; - 1} \right): - 1 = \frac{1}{{0 - 1}} \Leftrightarrow   1 =- 1\) (vô lý)

Chọn  A.

Phương pháp giải:

Hàm số \(\frac{1}{{f\left( x \right)}}\) xác định \( \Leftrightarrow f\left( x \right) \ne 0.\)

Lời giải chi tiết:

Hàm số \(y = \frac{{3x - 1}}{{2x - 2}}\) xác định \( \Leftrightarrow 2x - 2 \ne 0 \Leftrightarrow x \ne 1\)

Vậy TXĐ là \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)

Chọn  D.