Phương pháp giải:

Bước 1: Gọi số phức \(z=x+yi\) có điểm biểu diễn là \(M(x;y)\)

Bước 2: Thay z vào đề bài \(\Rightarrow \) Sinh ra một phương trình:

+) Đường thẳng: \(Ax+By+C=0.\)

+) Đường tròn: \({{x}^{2}}+{{y}^{2}}-2ax-2by+c=0.\)

+) Parabol: \(y=a.{{x}^{2}}+bx+c\)

+) Elip: \(\frac{{{x}^{2}}}{a}+\frac{{{y}^{2}}}{b}=1\)

Lời giải chi tiết:

Giả sử \(z=a+bi\) , ta có \({{z}^{2}}={{(a+bi)}^{2}}={{a}^{2}}-{{b}^{2}}+2abi\).

Số phức \({{z}^{2}}\) có điểm biểu diễn nằm trên trục tung khi \({{a}^{2}}-{{b}^{2}}=0\Leftrightarrow a=\pm b\).

Chọn đáp án D.

Phương pháp giải:

Phương pháp tìm tập hợp điểm biểu diễn số phức

Bước 1: Gọi số phức \(z=x+yi\) có điểm biểu diễn là \(M(x;y)\)

Bước 2: Thay z vào đề bài \(\Rightarrow \) Sinh ra một phương trình:

+) Đường thẳng: \(Ax+By+C=0.\)

+) Đường tròn: \({{x}^{2}}+{{y}^{2}}-2ax-2by+c=0.\)

+) Parabol: \(y=a.{{x}^{2}}+bx+c\)

+) Elip: \(\frac{{{x}^{2}}}{a}+\frac{{{y}^{2}}}{b}=1\)

Lời giải chi tiết:

Giả sử ta có số phức \(z=a+bi\) . Thay vào \(|z-(3-4i)|=2\) có

\(|a+bi-(3-4i)|=2\Leftrightarrow |(a-3)+(b+4)i|=2\Leftrightarrow \sqrt{{{(a-3)}^{2}}+{{(b+4)}^{2}}}=2\Leftrightarrow {{(a-3)}^{2}}+{{(b+4)}^{2}}=4\)

Chọn đáp án A 

Phương pháp giải:

Phương pháp tìm tập hợp điểm biểu diễn số phức

Bước 1: Gọi số phức \(z=x+yi\) có điểm biểu diễn là \(M(x;y)\)

Bước 2: Thay z vào đề bài \(\Rightarrow \) Sinh ra một phương trình:

+) Đường thẳng: \(Ax+By+C=0.\)

+) Đường tròn: \({{x}^{2}}+{{y}^{2}}-2ax-2by+c=0.\)

+) Parabol: \(y=a.{{x}^{2}}+bx+c\)

+) Elip: \(\frac{{{x}^{2}}}{a}+\frac{{{y}^{2}}}{b}=1\)

Lời giải chi tiết:

Giả sử ta có số phức \(z=a+bi.\) Thay vào \(|z-i|=1\) có

\(|a+bi-i|=1 \Leftrightarrow |a+(b-1)i|=1\Leftrightarrow {{a}^{2}}+{{(b-1)}^{2}}=1.\)

Chọn đáp án D 

Phương pháp giải:

Phương pháp tìm tập hợp điểm biểu diễn số phức

Bước 1: Gọi số phức \(z=x+yi\)có điểm biểu diễn là \(M(x;y)\)

Bước 2: Thay z vào đề bài \(\Rightarrow \)Sinh ra một phương trình:

+) Đường thẳng: \(Ax+By+C=0.\)

+) Đường tròn: \({{x}^{2}}+{{y}^{2}}-2ax-2by+c=0.\)

+) Parabol: \(y=a.{{x}^{2}}+bx+c\)

+) Elip: \(\frac{{{x}^{2}}}{a}+\frac{{{y}^{2}}}{b}=1\)

Lời giải chi tiết:

Giả sử ta có số phức \(z=x+yi\) . Ta có \({{z}^{2}}={{(x+yi)}^{2}}={{x}^{2}}-{{y}^{2}}+2xyi\).

\({{z}^{2}}\) là số thực âm \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} - {y^2} < 0}&{}\\{xy = 0}&{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}&{}\\{y \ne 0}&{}\end{array}} \right..\)

Chọn C

Phương pháp giải:

Phương pháp tìm tập hợp điểm biểu diễn số phức

Bước 1: Gọi số phức \(z=x+yi\)có điểm biểu diễn là \(M(x;y)\)

Bước 2: Thay zvào đề bài \(\Rightarrow \)Sinh ra một phương trình:

+) Đường thẳng: \(Ax+By+C=0.\)

+) Đường tròn: \({{x}^{2}}+{{y}^{2}}-2ax-2by+c=0.\)

+) Parabol: \(y=a.{{x}^{2}}+bx+c\)

+) Elip: \(\frac{{{x}^{2}}}{a}+\frac{{{y}^{2}}}{b}=1\)

Lời giải chi tiết:

Giả sử ta có số phức \(z=x+yi\). Ta có \(z(1+i)=(x+yi)(1+i)=(x-y)+(x+y)i\)

\(z(1+i)\) là số thực khi \(x+y=0\).

Chọn C

Phương pháp giải:

Phương pháp tìm tập hợp điểm biểu diễn số phức

Bước 1: Gọi số phức \(z=x+yi\)có điểm biểu diễn là \(M(x;y)\)

Bước 2: Thay zvào đề bài \(\Rightarrow \)Sinh ra một phương trình:

+) Đường thẳng: \(Ax+By+C=0.\)

+) Đường tròn: \({{x}^{2}}+{{y}^{2}}-2ax-2by+c=0.\)

+) Parabol: \(y=a.{{x}^{2}}+bx+c\)

+) Elip: \(\frac{{{x}^{2}}}{a}+\frac{{{y}^{2}}}{b}=1\)

Lời giải chi tiết:

Giả sử \(z=a+bi\) , ta có \({{z}^{2}}={{(a+bi)}^{2}}={{a}^{2}}-{{b}^{2}}+2abi\).

Số phức \({{z}^{2}}\) có điểm biểu diễn nằm trên trục hoành khi \(2ab = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a = 0}\\{b = 0}\end{array}} \right..\)

Chọn đáp án D.

Phương pháp giải:

Điểm \(M\left( {a;b} \right)\) là điểm biểu diễn cho số phức \(z = a + bi\).

Lời giải chi tiết:

Điểm biểu diễn của số phức \(z = 7 + bi\) với \(b \in \mathbb{R}\) là \(M\left( {7;b} \right),\,\,b \in \mathbb{R}\).

\(M\left( {7;b} \right),\,\,b \in \mathbb{R}\) thuộc đường thẳng \(x = 7\,\,\forall b \in \mathbb{R}\).

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

Vì các học sinh lớp 10A1 đều học giỏi ít nhất một trong hai môn Toán hoặc Tiếng Anh nên số học sinh của lớp là: \(30 + 25 - 16 = 39\) (học sinh).

Chọn  B.

Phương pháp giải:

Nếu \(\left| {z - \left( {{x_0} + {y_0}i} \right)} \right| = R,\,\,\left( {{x_0},{y_0},R \in \mathbb{R},\,\,R > 0} \right)\) thì tập hợp các điểm biểu diễn của z là đường tròn tâm \(I\left( {{x_0};{y_0}} \right)\), bán kính \(R\).

Lời giải chi tiết:

Tập hợp các điểm biểu diễn của số phức z trên mặt phẳng tọa độ là đường tròn tâm \(I\left( {0;1} \right)\), bán kính \(R = 3\). Khi đó: \(\left| {z - i} \right| = 3\).

Chọn: B

Phương pháp giải:

Lời giải chi tiết:

Chọn D

Phương pháp giải:

Điểm biểu diễn cho số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) là \(M\left( {a;b} \right)\).

Lời giải chi tiết:

Điểm biểu diễn của số phức \(z = 2019 + bi\) (\(b\) là số thực tùy ý) là \(M\left( {2019;b} \right)\).

Điểm \(M\left( {2019;b} \right)\) luôn thuộc đường thẳng \(x = 2019\) vói mọi \(b\) tùy ý.

Chọn B.

Phương pháp giải:

Gọi số phức \(z = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right).\)

Biến đổi điều kiện: \(\left| {2z - 1} \right| = 1\) để tìm quỹ tích của số phức \(z.\)

Lời giải chi tiết:

Gọi số phức \(z = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right).\)

Theo đề bài ta có: \(\left| {2z - 1} \right| = 1\)

\(\begin{array}{l} \Leftrightarrow \left| {2\left( {x + yi} \right) - 1} \right| = 1\\ \Leftrightarrow \left| {2x - 1 + 2yi} \right| = 1\\ \Leftrightarrow \sqrt {{{\left( {2x - 1} \right)}^2} + 4{y^2}}  = 1\\ \Leftrightarrow {\left( {2x - 1} \right)^2} + 4{y^2} = 1\\ \Leftrightarrow 4{\left( {x - \dfrac{1}{2}} \right)^2} + 4{y^2} = 1\\ \Leftrightarrow {\left( {x - \dfrac{1}{2}} \right)^2} + {y^2} = \dfrac{1}{4}\end{array}\)

\( \Rightarrow \) Quỹ tích của số phức \(z\) là đường tròn tâm \(I\left( {\dfrac{1}{2};\,\,0} \right)\) và bán kính \(R = \dfrac{1}{2}.\)

Chọn B.

Phương pháp giải:

Tập hợp các số phức \(z\) thỏa mãn \(\left| {z - \left( {a + bi} \right)} \right| = R\) là đường tròn tâm \(I\left( {a;b} \right)\), bán kính \(R\).

Lời giải chi tiết:

Tập hợp các số phức \(z\) thỏa mãn \(\left| {z - 3 + 2i} \right| = 4 \Leftrightarrow \left| {z - \left( {3 - 2i} \right)} \right| = 4\) là đường tròn tâm \(I\left( {3; - 2} \right)\), bán kính \(R = 4\).

Chọn D.

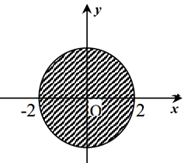
Phương pháp giải:

Điểm biểu diễn số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) là \(M\left( {a;\,\,b} \right).\)

Dựa vào đồ thị hàm số, viết phương trình đường tròn trên đồ thị.

Lời giải chi tiết:

Điểm biểu diễn số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) là \(M\left( {a;\,\,b} \right).\)

Ta thấy tập hợp các điểm biểu diễn số phức \(z\) bài cho là hình tròn (không chứa biên) có tâm \(O\) và bán kính \(R = 2\)

\( \Rightarrow \) Điều kiện thỏa mãn bài toán là: \({a^2} + {b^2} < 4.\) 

Chọn A.

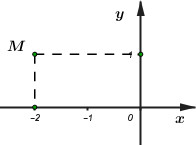
Phương pháp giải:

Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow M\left( {a;\,\,b} \right)\)  là điểm biểu diễn số phức \(z.\)

Lời giải chi tiết:

Dựa vào đồ thị hàm số ta thấy điểm \(M\left( { - 2;\,\,1} \right) \Rightarrow z =  - 2 + i.\)

\( \Rightarrow {\left( {1 + z} \right)^2} = {\left( {1 - 2 + i} \right)^2} = {\left( {i - 1} \right)^2} = {i^2} - 2i + 1 =  - 2i.\)

Chọn A.

Phương pháp giải:

Tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| {z - \left( {a + bi} \right)} \right| = R\) là đường tròn có tâm \(I\left( {a;b} \right)\) và bán kính \(R\).

Lời giải chi tiết:

Tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| {z - 1 + 2i} \right| = 2 \Leftrightarrow \left| {z - \left( {1 - 2i} \right)} \right| = 2\) là đường tròn có tâm \(I\left( {1; - 2} \right)\) và bán kính \(R = 2\).

Chọn A.

Phương pháp giải:

Tính \({z_1} + 2{z_2}\) và suy ra điểm biểu diễn.

Lời giải chi tiết:

Ta có: \({z_1} + 2{z_2} = \left( {1 + i} \right) + 2\left( {2 + i} \right) = 1 + i + 4 + 2i = 5 + 3i\).

Do đó điểm biểu diễn số phức trên là \(\left( {5;3} \right)\).

Chọn D.

Phương pháp giải:

Gọi \(z = x + yi\left( {x;y \in R} \right)\) khi đó \(\overline z  = x - yi\)

Từ đó nhân hai số phức để tìm tập hợp điểm

Lời giải chi tiết:

Gọi \(z = x + yi\left( {x;y \in R} \right)\) khi đó \(\overline z  = x - yi\)

Ta có: \(z.\overline z  = 1 \Leftrightarrow \left( {x + yi} \right)\left( {x - yi} \right) = 1\)\( \Leftrightarrow {x^2} - {\left( {yi} \right)^2} = 1\)\( \Leftrightarrow {x^2} + {y^2} = 1\)

Vậy tập hợp điểm biểu diễn số phức \(z\) là một đường tròn.

Chọn B.

Phương pháp giải:

Phương pháp tìm tập hợp điểm biểu diễn số phức

Bước 1: Gọi số phức \(z = x + yi\) có điểm biểu diễn là \(M(x;y)\)

Bước 2: Thay \(z\) vào đề bài \( \Rightarrow \) Sinh ra một phương trình:

+) Đường thẳng: \(Ax + By + C = 0.\)

+) Đường tròn: \({x^2} + {y^2} - 2ax - 2by + c = 0.\)

+) Parabol: \(y = a.{x^2} + bx + c\)

+) Elip: \(\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} = 1\)

Lời giải chi tiết:

Giả sử \(z = a + bi\), ta có \({z^2} = {\left( {a + bi} \right)^2} = {a^2} - {b^2} + 2abi\).

Số phức \({z^2}\) có điểm biểu diễn nằm trên trục tung khi \({a^2} - {b^2} = 0 \Leftrightarrow a =  \pm b\).

Vậy tập hợp các điểm biểu diễn số phức \(z\) là đường phân giác góc phần tư (I), (III) và đường phân giác góc phần tư (II), (IV).

Chọn D.

Phương pháp giải:

Tập hợp các số phức thỏa mãn \(\left| {z - \left( {a + bi} \right)} \right| = R\) là đường tròn tâm \(I\left( {a;b} \right)\) bán kính \(R\).

Lời giải chi tiết:

Tập hợp các số phức \(z\) thỏa mãn \(\left| {z + i} \right| = 2 \Leftrightarrow \left| {z - \left( { - i} \right)} \right| = 2\)  là đường tròn tâm \(I\left( {0; - 1} \right)\), bán kính \(R = 2\).

Đường tròn đó có phương trình là: \({x^2} + {\left( {y + 1} \right)^2} = 4\).

Chọn B.

Phương pháp giải:

- Đặt \(z = a + bi\), thay vào các điều kiện bài cho lập hệ phương trình ẩn \(x,y\).

- Giải hệ phương trình tìm \(x,y \Rightarrow z\).

Lời giải chi tiết:

Đặt \(z = a + bi\) ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}\left| z \right| = 5\\\left| {z - \left( {7 + 7i} \right)} \right| = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} = 25\\{\left( {a - 7} \right)^2} + {\left( {b - 7} \right)^2} = 25\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} = 25\\{a^2} + {b^2} - 14a - 14b + 98 = 25\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} = 25\\a + b = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 7 - a\\{a^2} + {\left( {7 - a} \right)^2} = 25\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 7 - a\\2{a^2} - 14a + 24 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 4,b = 3\\a = 3,b = 4\end{array} \right.\end{array}\)

  \( \Rightarrow \) hai số phức cần tìm là \(4 + 3i,3 + 4i \Rightarrow T = {\left| {{z_1} - {z_2}} \right|^2} = {\left| {\left( {4 + 3i} \right) - \left( {3 + 4i} \right)} \right|^2} = {\left| {1 - i} \right|^2} = 2\).

Chọn D.

Phương pháp giải:

Số phức \(z = x + yi\,\left( {x;y \in \mathbb{R}} \right)\) có mô đun \(\left| z \right| = \sqrt {{x^2} + {y^2}} \)

Lời giải chi tiết:

Gọi số phức \(z = x + yi\,\left( {x;y \in \mathbb{R}} \right)\) suy ra  \(\left| z \right| = \sqrt {{x^2} + {y^2}}  = \sqrt 7  \Leftrightarrow {x^2} + {y^2} = 7\)

Tập hợp điểm biểu diễn số phức \(z\) là đường tròn tâm \(O\left( {0;0} \right)\) bán kính \(R = \sqrt 7 \).

Chọn D

Phương pháp giải:

Sử dụng phương pháp hình học.

Lời giải chi tiết:

Giả sử \(M,{F_1},{F_2}\) lần lượt là điểm biểu diễn của các số phức \(z,\,\,{z_1} = 1,\,\,\,{z_2} =  - 2i\)

Khi đó \(\left| {z - 1} \right| + \left| {z + 2i} \right| = 2\sqrt 2  \Leftrightarrow M{F_1} + M{F_2} = 2\sqrt 2 \)

\( \Rightarrow \) Tập hợp những điểm biểu diễn số phức z là Một đường Elip.

Chọn: C

Phương pháp giải:

Số phức \(z = x + yi\,\,\left( {x;y \in \mathbb{R}} \right)\) có phần thực là \(x\) và phần ảo là \(y.\)

Lời giải chi tiết:

Số phức \(z = x + yi\,\,\left( {x;y \in \mathbb{R}} \right)\) có phần thực là \(x = 3\) nên tập hợp điểm biểu diễn số phức \(z\) là đường thẳng \(x = 3.\)

Chọn D

Phương pháp giải:

Sử dụng phương pháp hình học.

Lời giải chi tiết:

Gọi \(z = x + yi\,\,\,\left( {x;\,\,y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\,\,y} \right)\) là điểm biểu diễn số phức \(z.\)

\(\left| {z - 3} \right| + \left| {z + 3} \right| = 10 \Leftrightarrow M{F_1} + M{F_2} = 10 = 2a\)

Với \({F_1}\left( {3;\,\,0} \right),\,\,\,{F_2}\left( { - 3;\,\,0} \right),\,\,\,a = 5 \Rightarrow c = 3 \Rightarrow {b^2} = {a^2} - {c^2} = 16.\)  

\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức thỏa mãn \(\left| {z - 3} \right| + \left| {z + 3} \right| = 10\) là elip \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)

 \( \Rightarrow {z_1},{z_2}\) là hai số phức thuộc S có môđun nhỏ nhất khi và chỉ khi điểm biểu diễn của \({z_1},{z_2}\) lần lượt là \(A\left( {4;0} \right),B\left( { - 4;0} \right)\).

\( \Rightarrow {z_1} = 4i,\,\,{z_2} =  - 4i\,\, \Rightarrow P = z_1^2 + z_2^2 =  - 32\).

Chọn: C  

Phương pháp giải:

Giả sử \(z = x + yi,\,\,\left( {x,y \in \mathbb{R}} \right)\), biến đổi và kết luận.

Lời giải chi tiết:

Giả sử \(z = x + yi,\,\,\left( {x,y \in \mathbb{R}} \right)\), ta có:

\(\begin{array}{l}\,\,\,\,\left( {1 + x + yi} \right)\left( {1 - i\left( {x + yi} \right)} \right) = \left( {1 + x + yi} \right)\left( {1 + y - xi} \right)\\ = \left( {1 + x} \right)\left( {1 + y} \right) + \left( {y\left( {1 + y} \right) - x\left( {1 + x} \right)} \right)i + xy\end{array}\)

Do \(\left( {1 + z} \right)\left( {1 - iz} \right)\) là số thực nên \(y\left( {1 + y} \right) - x\left( {1 + x} \right) = 0 \Leftrightarrow {\left( {x + \dfrac{1}{2}} \right)^2} = {\left( {y + \dfrac{1}{2}} \right)^2} \Leftrightarrow \left[ \begin{array}{l}x - y = 0\\x + y + 1 = 0\end{array} \right.\)

Vậy tập hợp các điểm biểu diễn của số phức z là: Hai đường thẳng.

Chọn: D

Phương pháp giải:

Sử dụng phương pháp hình học.

Lời giải chi tiết:

Số phức \(z = x + yi,\left( {x,y \in \mathbb{R}} \right)\) có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4 \Rightarrow  - 1 \le x \le 3\).

\(w = z + \overline z  + 2i = x + yi + x - yi + 2i = 2x + 2i\)

Tọa độ điểm biểu diễn số phức \(w\) là \(M\left( {x;2} \right),\,\,x \in \left[ { - 1;3} \right]\)

Vậy, tập hợp các điểm biểu diễn của số phức là \(w\) là đoạn thẳng \(AB\) với \(A\left( { - 1;2} \right),\,B\left( {3;2} \right)\).

Chọn: B

Phương pháp giải:

Tập hợp các số phức z thỏa mãn \(\left| {z - \left( {a + bi} \right)} \right| = R\) thuộc đường tròn tâm \(I\left( {a;b} \right)\) bán kính \(R\).

Lời giải chi tiết:

\(\left| {z + 2 - 5i} \right| = 6 \Rightarrow \left| {z - \left( { - 2 + 5i} \right)} \right| = 6\).

Vậy tập hợp điểm biểu diễn số phức \(z\) thỏa mãn điều kiện\(\left| {z + 2 - 5i} \right| = 6\) là đường tròn có tâm và bán kính lần lượt là \(I\left( { - 2;5} \right),\,\,R = 6\).

Chọn A

Phương pháp giải:

Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức \(z\) thỏa mãn \(\left| {z - \left( {a + bi} \right)} \right| = R\) là đường tròn có tâm \(I\left( {a;b} \right)\), bán kính \(R\).

Lời giải chi tiết:

Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức \(z\) thỏa mãn \(\left| {z + 4 - 8i} \right| = 2\sqrt 5 \) là đường tròn có tâm \(I\left( { - 4;8} \right)\), bán kính \(R = 2\sqrt 5 \) nên có phương trình \({\left( {x + 4} \right)^2} + {\left( {y - 8} \right)^2} = 20\).

Chọn D

Phương pháp giải:

- Tìm tập hợp điểm biểu diễn số phức \(z\).

- Sử dụng điều kiện hình học để tìm số phức \(z\) có mô đun lớn nhất.

Lời giải chi tiết:

Gọi \(z = x + yi\). Ta có \(\left| {z + 4 - 3i} \right| = 5 \Leftrightarrow \left| {\left( {x + 4} \right) + \left( {y - 3} \right)i} \right| = 5\)\( \Leftrightarrow {\left( {x + 4} \right)^2} + {\left( {y - 3} \right)^3} = 25\).

Vậy biểu diễn của số phức \(z\) là đường tròn tâm \(I\left( { - 4;\,3} \right)\), bán kính \(R = 5\).

\(M\) là điểm biểu diễn của số phức \(z\) có mô đun lớn nhất. Khi đó \(M\) là giao điểm của đường tròn \(\left( C \right)\) và đường thẳng \(OI:y =  - x\). Suy ra \(M\left( { - 8;\,6} \right)\).

Chọn D.

Phương pháp giải:

Tập hợp các điểm biểu diễn số phức z thỏa mãn: \(\left| {z - \left( {a + bi} \right)} \right| = r,\,\,\left( {r > 0} \right)\) là đường tròn tâm \(I\left( {a;b} \right)\), bán kính r.

Lời giải chi tiết:

Giả sử :

Ta có:

\(\begin{array}{l}w = \left( {8 - 6i} \right)z + 2i \Leftrightarrow \left( {8 - 6i} \right)z = w - 2i \Rightarrow \left| {\left( {8 - 6i} \right)z} \right| = \left| {w - 2i} \right|\\ \Leftrightarrow \left| {8 - 6i} \right|.\left| z \right| = \left| {w - 2i} \right| \Leftrightarrow \left| {w - 2i} \right| = 10.12 \Leftrightarrow \left| {w - 2i} \right| = 120\end{array}\)

\( \Rightarrow \) Tập hợp các điểm biểu diễn các số phức \(w\) là đường tròn tâm \(I\left( {0;2} \right)\), bán kính \(r = 120\).

Chọn: A

Phương pháp giải:

Tập hợp các điểm biểu diễn của các số phức thỏa mãn \(\left| {z - a - bi} \right| = R,\,\,R > 0\) là đường tròn: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\).

Lời giải chi tiết:

Tập hợp các điểm M biểu diễn của các số phức thỏa mãn \(\left| {z - 1 - 3i} \right| = 2\) là đường tròn: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4\)

 là khoảng cách từ điểm M đến điểm \(A\left( {1;0} \right)\). Khoảng cách này nhỏ nhất khi và chỉ khi M nằm giữa I và A (với \(I\left( {1;3} \right)\) là tâm đường tròn \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4\))

 Dễ dàng tính được \(M\left( {1;1} \right)\).

Vậy, số phức z thỏa mãn là \(z = 1 + i\).

Chọn: B

Phương pháp giải:

Nếu \(\left| {z - \left( {{x_0} + {y_0}i} \right)} \right| = R,\,\,\left( {{x_0},{y_0},R \in \mathbb{R},\,\,R > 0} \right)\) thì tập hợp các điểm biểu diễn của z là đường tròn tâm \(I\left( {{x_0};{y_0}} \right)\), bán kính \(R\).

Lời giải chi tiết:

Giả sử \(z = a + bi,\,\left( {a,b \in \mathbb{R}} \right)\) có điểm biểu diễn là \(M\left( {a;b} \right)\), thỏa mãn điều kiện:  \(\left| {z - \left( {3 + 2i} \right)} \right| = 2\)

Khi đó, \(\sqrt {{{\left( {a - 3} \right)}^2} + {{\left( {b - 2} \right)}^2}}  = 2 \Leftrightarrow {\left( {a - 3} \right)^2} + {\left( {b - 2} \right)^2} = {2^2}\)

Vậy, tập hợp các điểm biểu diễn các số phức z là đường tròn tâm \(I\left( {3;2} \right)\), bán kính \(R = 2\).

Chọn: A

Phương pháp giải:

Tập hợp các điểm biểu diễn số phức z thỏa mãn: \(\left| {z - \left( {a + bi} \right)} \right| = \left| {z - \left( {a' + b'i} \right)} \right|,\,\,\left( {a,b,a',b' \in \mathbb{R}} \right)\) là đường trung trực của đoạn thẳng \(AA'\) với  \(A\left( {a;b} \right),\,A'\left( {a';b'} \right)\).

Lời giải chi tiết:

Ta có:  \(\left| {z - 1 + 3i} \right| = \left| {z - 2 - i} \right| \Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 3} \right)}^2}}  = \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 1} \right)}^2}} \)

\( \Rightarrow \)  Tập hợp điểm \(M\left( {x;y} \right)\) biểu diễn của số phức \(z = x + yi,\,\,\left( {x,y \in \mathbb{R}} \right)\) là đường thẳng trung trực của đoạn thẳng AB với \(A\left( {1; - 3} \right),\,B\left( {2;1} \right)\).

Chọn: B

Phương pháp giải:

Sử dụng kiến thức: Điểm \({M_1},{M_2}\) lần lượt biểu diễn các số phức \({z_1},{z_2}\) thì \(\left| {{z_1} - {z_2}} \right| = {M_1}{M_2}\).

Lời giải chi tiết:

Giả sử điểm \(M\) là điểm biểu diễn số phức \(z\).  Điểm \(I\left( { - 1;\,2} \right)\) là điểm biểu diễn số phức \({z_1} =  - 1 + 2i\).

Ta có \(\left| {z + 1 - 2i} \right| = 3\)\( \Leftrightarrow \left| {z - \left( { - 1 + 2i} \right)} \right| = 3 \Leftrightarrow IM = 3\).

Tập hợp điểm \(M\) là điểm biểu diễn số phức \(z\) là đường tròn tâm \(I\left( { - 1;\,2} \right)\), bán kính \(r = 3\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Chọn C.

Phương pháp giải:

+) \(M\left( {a;b} \right)\) là điểm biểu diễn cho số phức \(z = a + bi\) trên mặt phẳng phức, từ đó xác định tọa độ các điểm A, B, C.

+) Gọi \(D\left( {x;y} \right)\).

+) Để ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB}  = \overrightarrow {DC} \). Sử dụng điều kiện để hai vector bằng nhau.

Lời giải chi tiết:

A, B, C lần lượt là các điểm biểu diễn của các số phức \({z_1} = 2 + 3i;\,\,{z_2} = 1 + 5i\); \({z_3} = 4 + i\).

\( \Rightarrow A\left( {2;3} \right);\,\,B\left( {1;5} \right);\,\,C\left( {4;1} \right)\)

Để ABCD là hình bình hành \( \Rightarrow \overrightarrow {AB}  = \overrightarrow {DC} \). Gọi \(D\left( {x;y} \right)\) ta có \(\overrightarrow {AB}  = \left( { - 1;2} \right);\,\,\overrightarrow {DC}  = \left( {4 - x;1 - y} \right)\).

\( \Rightarrow \left\{ \begin{array}{l}4 - x =  - 1\\1 - y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y =  - 1\end{array} \right. \Rightarrow D\left( {5; - 1} \right)\)

\( \Rightarrow \) Số phức biểu diễn cho điểm D là \({z_4} = 5 - i\) có phần ảo là -1.

Chọn B.

Phương pháp giải:

+) Xác định tọa độ các điểm A, B.

+) Gọi \(C\left( {x;y} \right)\). Tam giác ABC vuông tại C \( \Rightarrow \overrightarrow {AC} .\overrightarrow {BC}  = 0\)

+) Thử lần lượt các đáp án và chọn đáp án đung.

Lời giải chi tiết:

A, B lần lượt biểu diễn các số phức \({z_1} =  - 2 - 4i;\,\,{z_2} = 2 - 2i \Rightarrow A\left( { - 2; - 4} \right);\,\,B\left( {2; - 2} \right)\)

Gọi \(C\left( {x;y} \right) \Rightarrow \overrightarrow {AC}  = \left( {x + 2;y + 4} \right);\,\,\overrightarrow {BC}  = \left( {x - 2;y + 2} \right)\)

Do tam giác ABC vuông tại C \( \Rightarrow \overrightarrow {AC} .\overrightarrow {BC}  = 0\)

\( \Leftrightarrow \left( {x + 2} \right)\left( {x - 2} \right) + \left( {y + 4} \right)\left( {y + 2} \right) = 0\,\,\left( * \right)\)

Đáp án A: \(C\left( {2; - 4} \right)\) thỏa mãn (*)

Đáp án B: \(C\left( {2; - 2} \right) \equiv B \Rightarrow \) loại

Đáp án C: \(C\left( { - 2;2} \right)\) không thỏa mãn (*)

Đáp án D: \(C\left( {2;2} \right)\) không thỏa mãn (*).

Chọn A.

Phương pháp giải:

Tập hợp các điểm M thuộc elip có hai tiêu điểm \({F_1};\,\,{F_2}\) thỏa mãn \(M{F_1} + M{F_2} = 2a\).

Lời giải chi tiết:

Gọi M là điểm biểu diễn cho số phức z, \({F_1}\left( {1;0} \right)\) là điểm biểu diễn cho số phức \({z_1} = 1\); \({F_2}\left( {0;\sqrt 3 } \right)\) là điểm biểu diễn cho số phức \({z_2} = \sqrt 3 i\).

Ta có

\(\begin{array}{l}\,\,\,\,\,\,\left| {z - {z_1}} \right| + \left| {z - {z_2}} \right| = 2\\ \Leftrightarrow \left| {\overrightarrow {OM}  - \overrightarrow {O{F_1}} } \right| + \left| {\overrightarrow {OM}  - \overrightarrow {O{F_2}} } \right| = 2\\ \Leftrightarrow M{F_1} + M{F_2} = 2\end{array}\)

Tập hợp các điểm M thỏa mãn \(M{F_1} + M{F_2} = 2\) là đường elip có 2 tiêu điểm \({F_1}\left( {1;0} \right);\,\,{F_2}\left( {0;\sqrt 3 } \right)\).

Vậy tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện \(\left| {z - 1} \right| + \left| {z - \sqrt 3 i} \right| = 2\) là đường elip có 2 tiêu điểm \({F_1}\left( {1;0} \right);\,\,{F_2}\left( {0;\sqrt 3 } \right)\).

Chọn D.

Phương pháp giải:

Gọi \(z = x + yi\), tìm biểu thức thể hiện mối liên hệ giữa \(x,\,\,y\).

Lời giải chi tiết:

Đặt \(z = x + yi\,\,\left( {x,y \in \mathbb{R}} \right)\). Theo bài ra ta có:

\(\left| {x + yi - 2 + i} \right| = 4 \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 16\)

Vậy tập hợp các điểm biểu diễn các số phức \(z\) là một đường tròn có tâm \(I\left( {2;1} \right)\), bán kính \(R = 4\).

Chọn D.