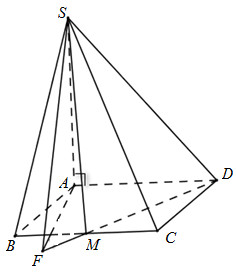
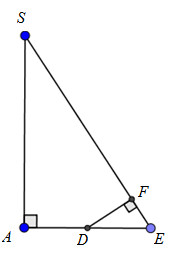
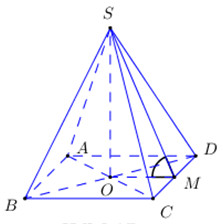
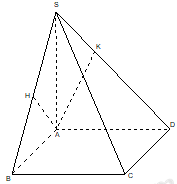
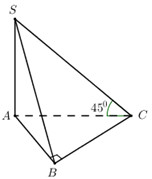
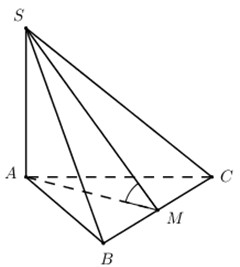
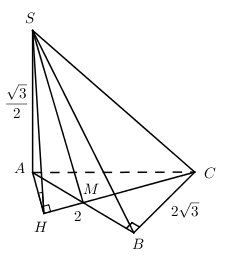
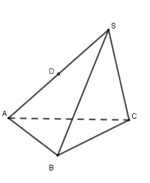
40 bài tập hai mặt phẳng vuông góc mức độ vận dụngLàm bàiCâu hỏi 1 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh SA vuông góc với mặt phẳng (ABCD), \(SA = AB = a,AD = 3a.\) Gọi M là trung điểm của BC. Tính cosin góc tạo bởi hai mặt phẳng (ABCD) và (SDM)?
Đáp án: B Phương pháp giải: +) Trong (ABCD) kẻ \(AF \bot MD\). +) Chứng minh góc giữa hai mặt phẳng cần tìm là góc SFA. +) Tính các cạnh AF, SF và tính \(\cos \widehat {SFA}\). Lời giải chi tiết:
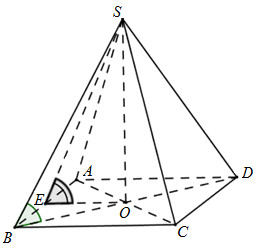
Trong (ABCD) kẻ \(AF \bot MD\). Lại có: \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot MD\) \( \Rightarrow MD \bot \left( {SAF} \right) \Rightarrow MD \bot SF\) Ta có: \(\left. \begin{array}{l}\left( {SDM} \right) \cap \left( {ABCD} \right) = MD\\SF \bot MD\\AF \bot MD\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SDM} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SF;AF} \right)} = \widehat {SFA}\) Xét tam giác vuông CMD có: \(MD = \sqrt {C{D^2} + M{C^2}} = \sqrt {{a^2} + {{\left( {\dfrac{3}{2}a} \right)}^2}} = \dfrac{{a\sqrt {13} }}{2}\) Ta có: \({S_{\Delta AMD}} = \dfrac{1}{2}.3a.a = \dfrac{3}{2}{a^2} = \dfrac{1}{2}AF.MD \Rightarrow AF = \dfrac{{2{S_{\Delta ADM}}}}{{MD}} = \dfrac{{3{a^2}}}{{\dfrac{{a\sqrt {13} }}{2}}} = \dfrac{{6a}}{{\sqrt {13} }}\) Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AF\). Suy ra tam giác SAF vuông tại A \(\begin{array}{l} \Rightarrow SF = \sqrt {A{F^2} + S{A^2}} = \sqrt {{a^2} + \dfrac{{36}}{{13}}{a^2}} = \dfrac{{7a}}{{\sqrt {13} }}\\ \Rightarrow cos\widehat {SFA} = \dfrac{{AF}}{{SF}} = \dfrac{{6a}}{{\sqrt {13} }}\dfrac{{\sqrt {13} }}{{7a}} = \dfrac{6}{7}\end{array}\) Chọn B. Câu hỏi 2 : Cho hình vuông ABCD cạnh a, tâm O và \(SA \bot \left( {ABCD} \right)\). Để góc giữa \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\)bằng \({60^0}\)thì độ dài của SA là:
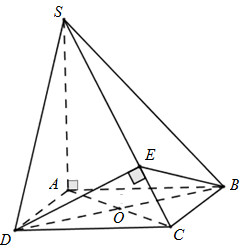
Đáp án: A Phương pháp giải: Trong \(\left( {SCD} \right)\) kẻ \(DE \bot SC\). Chứng minh \(\widehat {\left( {\left( {SBC} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {DE;BE} \right)} \Rightarrow \left[ \begin{array}{l}\widehat {DEB} = {60^0}\\\widehat {DEB} = {120^0}\end{array} \right.\) Lời giải chi tiết:
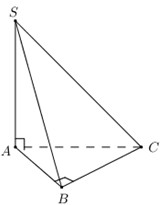
Ta có: \(\left. \begin{array}{l}BD \bot SA\\BD \bot AC\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\) Trong \(\left( {SCD} \right)\) kẻ \(DE \bot SC \Rightarrow SC \bot \left( {BDE} \right) \Rightarrow SC \bot BE\) \(\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {SCD} \right) = SC\\DE \bot SC\\BE \bot SC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {DE;BE} \right)} = {60^0}\) \(\left. \begin{array}{l}CD \bot SA\\CD \bot AD\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD \Rightarrow \Delta SCD\) vuông tại D \( \Rightarrow \dfrac{1}{{D{E^2}}} = \dfrac{1}{{D{C^2}}} + \dfrac{1}{{S{D^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{S{A^2} + {a^2}}}\) Ta có: \(DE = BE \Rightarrow \Delta EBD\) cân tại E Nếu \(\widehat {DEB} = {60^0} \Rightarrow \Delta EBD\)đều\( \Rightarrow DE = BD = a\sqrt 2 \) \( \Rightarrow \dfrac{1}{{2{a^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{S{A^2} + {a^2}}} \Rightarrow \dfrac{1}{{S{A^2} + {a^2}}} = - \dfrac{1}{{2{a^2}}}\) (vô lý) \( \Rightarrow \widehat {DEB} = {120^0} \Rightarrow \widehat {EDB} = {30^0}\) \(\Delta EBD\) cân tại E, O là trung điểm của BD \( \Rightarrow EO \bot BD \Rightarrow DE = \dfrac{{DO}}{{cos30}} = \dfrac{{a\sqrt 2 }}{2}\dfrac{2}{{\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{3}\) \( \Rightarrow \dfrac{3}{{2{a^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{S{A^2} + {a^2}}} \Rightarrow \dfrac{1}{{S{A^2} + {a^2}}} = \dfrac{1}{{2{a^2}}} \Rightarrow S{A^2} + {a^2} = 2{a^2} \Rightarrow S{A^2} = {a^2} \Rightarrow SA = a\) Chọn A. Câu hỏi 3 : Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, có \(AB = 2a,\) \(AD = DC = a,\) \(SA = a\) và \(SA \bot \left( {ABCD} \right)\). Tan của góc giữa hai mặt phẳng \(\left( {SBC} \right)\)và \(\left( {ABCD} \right)\) là:
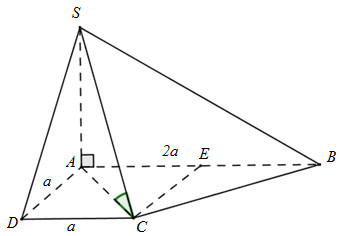
Đáp án: D Phương pháp giải: Chứng minh SC và AC cùng vuông góc với giao tuyến BC. Lời giải chi tiết:
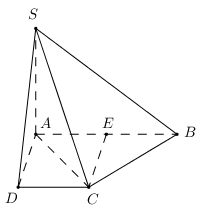
Xét tam giác \(CE = a = \frac{1}{2}AB \Rightarrow \Delta ACB\)vuông tại C (trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy) Ta có: \(\left. \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right\} \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot SC\) \(\begin{array}{l}\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\SC \bot BC\\AC \bot BC\end{array} \right\}\\ \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA}\end{array}\) (vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\)vuông tại A \( \Rightarrow \widehat {SCA} < {90^0}\)) Xét tam giác vuông ACD có: \(AC = \sqrt {A{D^2} + C{D^2}} = a\sqrt 2 \) Xét tam giác vuông SAC có: \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\) Chọn D. Câu hỏi 4 : Cho hình chóp S.ABCD có đáy \(ABCD\) là nửa lục giác đều nội tiếp đường tròn đường kính \(AB = 2a,SA = a\sqrt 3 \) và vuông góc với mặt phẳng ABCD. Cosin góc giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) là:
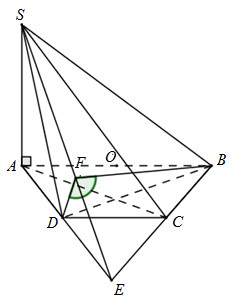
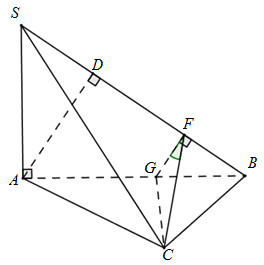
Đáp án: C Phương pháp giải: +) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC) +) Trong \(\left( {SAE} \right)\) kẻ \(DF \bot SE\) +) Chứng minh DF và BF cùng vuông góc với giao tuyến. Lời giải chi tiết:
Gọi \(E = AD \cap BC\) (vì \(\widehat {BFD} < {90^0}\)) Vì \(DB \bot \left( {SAD} \right) \Rightarrow DB \bot DF \Rightarrow \Delta BDF\)vuông tại D Xét tam giác vuông ABD có: \(BD = \sqrt {A{B^2} - A{D^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \) \(\Delta EAB\) đều nên \(AE = BE = AB = 2a \Rightarrow SE = \sqrt {S{A^2} + A{E^2}} = \sqrt {3{a^2} + 4{a^2}} = a\sqrt 7 \) D là trung điểm của AE nên \(AD = \frac{1}{2}AE = a\)
Ta có: \(\Delta EDF \sim \Delta ESA\left( {g.g} \right) \Rightarrow \dfrac{{DF}}{{SA}} = \dfrac{{DE}}{{SE}} \Rightarrow DF = \dfrac{{SA.DE}}{{SE}} = \dfrac{{a\sqrt 3 .a}}{{a\sqrt 7 }} = \dfrac{{a\sqrt 3 }}{{\sqrt 7 }}\) \( \Rightarrow BF = \sqrt {D{F^2} + B{D^2}} = \sqrt {\dfrac{3}{7}{a^2} + 3{a^2} = } \dfrac{{2\sqrt 6 a}}{{\sqrt 7 }}\) Vậy \(cos\widehat {BFD} = \dfrac{{DF}}{{BF}} = \dfrac{{\dfrac{{a\sqrt 3 }}{{\sqrt 7 }}}}{{\dfrac{{2\sqrt 6 a}}{{\sqrt 7 }}}} = \dfrac{{\sqrt 2 }}{4}\) Chọn C. Câu hỏi 5 : Cho chóp S.ABC có đáy ABC là tam giác đều cạnh \(a,SA \bot \left( {ABC} \right);SA = a\sqrt 3 \). Cosin của góc giữa hai mặt phẳng \(\left( {SAB} \right)\)và \(\left( {SBC} \right)\) là:
Đáp án: D Phương pháp giải: +) Trong \(\left( {SBC} \right)\) kẻ \(CF \bot SB\left( {F \in SB} \right)\), trong \(\left( {SAB} \right)\)kẻ \(GF \bot SB\left( {G \in AB} \right)\) +) Chứng minh \(\widehat {\left( {\left( {SAB} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {GF;CF} \right)}\) +) Sử dụng định lí Cosin trong tam giác. Lời giải chi tiết:
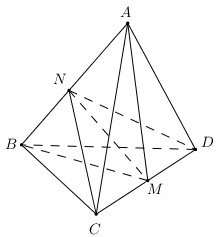
Trong \(\left( {SBC} \right)\) kẻ \(CF \bot SB\left( {F \in SB} \right)\), trong \(\left( {SAB} \right)\)kẻ \(GF \bot SB\left( {G \in AB} \right)\) \(\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\GF \bot SB\\CF \bot SB\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {GF;CF} \right)}\) Ta có: \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {3{a^2} + {a^2}} = 2a = SB\) Xét tam giác SBC có: \(cos\widehat {SBC} = \frac{{S{B^2} + B{C^2} - S{C^2}}}{{2.SB.BC}} = \frac{{4{a^2} + {a^2} - 4{a^2}}}{{2.2a.a}} = \frac{1}{4}\) \(\begin{array}{l} \Rightarrow BF = BC.cos\widehat {SBC} = \frac{1}{4}a\\ \Rightarrow CF = \sqrt {B{C^2} - B{F^2}} = \sqrt {{a^2} - \frac{1}{{16}}{a^2}} = \frac{{a\sqrt {15} }}{4}\end{array}\) Ta có: \(\begin{array}{l}\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \\ \Rightarrow GF = BF.tan\widehat {SBA} = \frac{{\sqrt 3 }}{4}a \Rightarrow BG = \sqrt {B{F^2} + G{F^2}} = \sqrt {\frac{{{a^2}}}{{16}} + \frac{{3{a^2}}}{{16}}} = \frac{a}{2}\end{array}\) \( \Rightarrow \)G là trung điểm của AB \( \Rightarrow GC = \frac{{a\sqrt 3 }}{2}\) \( \Rightarrow cos\widehat {CFG} = \dfrac{{G{F^2} + C{F^2} - G{C^2}}}{{2.GF.CF}} = \dfrac{{\dfrac{{3{a^2}}}{{16}} + \dfrac{{15{a^2}}}{{16}} - \dfrac{{3{a^2}}}{4}}}{{2.\dfrac{{a\sqrt 3 }}{4}.\dfrac{{a\sqrt {15} }}{4}}} = \dfrac{{\dfrac{3}{8}{a^2}}}{{\dfrac{{3\sqrt 5 {a^2}}}{8}}} = \dfrac{1}{{\sqrt 5 }}\) Chọn D. Câu hỏi 6 : Cho tứ diện S.ABC có SA, SB, SC đôi một vuông góc và \(SA = SB = SC\) . Gọi I, J lần lượt là trung điểm của AB, BC. Tính góc giữa hai mặt phẳng (SAJ) và (SCI)?
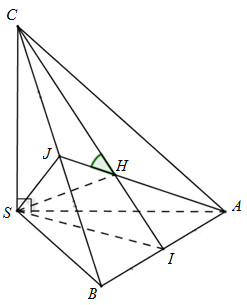
Đáp án: B Phương pháp giải: +) Chứng minh chóp S.ABC là chóp đều. +) Gọi H là tâm tam giác đều ABC \( \Rightarrow SH \bot \left( {ABC} \right)\) +) Chứng minh AJ và CI cùng vuông góc với giao tuyến SH. +) Sử dụng tính chất hai góc nhọn trong tam giác vuông phụ nhau. Lời giải chi tiết:
Vì \(SA = SB = SC\) nên \(AB = BC = CA\). Suy ra chóp S.ABC đều. Gọi H là tâm tam giác đều ABC\( \Rightarrow SH \bot \left( {ABC} \right) \Rightarrow SH \bot CI;SH \bot AJ\) Ta có: \(\left. \begin{array}{l}\left( {SAJ} \right) \cap \left( {SCI} \right) = SH\\AJ \bot SH\\CI \bot SH\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAJ} \right);\left( {SCI} \right)} \right)} = \widehat {\left( {AJ;CI} \right)} = \widehat {CHJ}\) (Vì tam giác CHJ vuông tại J nên \(\widehat {CHJ} < {90^0}\)) Vì tam giác ABC đều nên trung tuyến CI đồng thời là phân giác\( \Rightarrow \widehat {JCH} = {30^0}\) Xét tam giác vuông CHJ có: \(\widehat {CHJ} = {90^0} - \widehat {JCH} = {90^0} - {30^0} = {60^0}\) Chọn B. Câu hỏi 7 : Cho hình lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh a, và \(A'A = A'B = A'C = a\sqrt {\dfrac{7}{{12}}} .\) Tính góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {ABC} \right)\)?
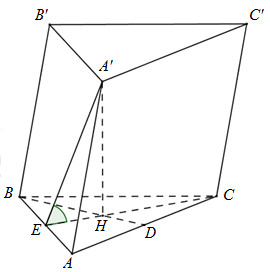
Đáp án: D Phương pháp giải: +) Gọi H là tâm của tam giác đều ABC\( \Rightarrow A'H \bot \left( {ABC} \right)\) +) Gọi E là trung điểm của AB, chứng minh \(\widehat {\left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {HE;A'E} \right)}\). Lời giải chi tiết:
Vì \(A'A = A'B = A'C = a\sqrt {\frac{7}{{12}}} ,\Delta ABC\)đều nên chóp\(A'.ABC\)là chóp đều. Gọi H là tâm của tam giác đều ABC\( \Rightarrow A'H \bot \left( {ABC} \right)\) Gọi E là trung điểm của AB thì \(HE \bot AB\) Lại có: \(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot AB\) \( \Rightarrow AB \bot \left( {A'HE} \right) \Rightarrow AB \bot A'E\) Ta có: \(\begin{array}{l}\left. \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {ABC} \right) = AB\\HE \bot AB\\AE \bot AB\end{array} \right\}\\ \Rightarrow \widehat {\left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {HE;A'E} \right)} = \widehat {A'EH}\end{array}\) (Vì \(\Delta A'HE\) vuông tại H \( \Rightarrow \widehat {A'EH} < {90^0}\)) Ta có: \(CE = \dfrac{{a\sqrt 3 }}{2} \Rightarrow HE = \dfrac{1}{3}CE = \dfrac{{a\sqrt 3 }}{6};HC = \dfrac{2}{3}CE = \dfrac{{a\sqrt 3 }}{3}\) \(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot CH\) Xét tam giác vuông\(A'HC\)có: \(A'H = \sqrt {A'{C^2} - H{C^2}} = \sqrt {\dfrac{7}{{12}}{a^2} - \dfrac{1}{3}{a^2}} = \dfrac{a}{2}\) Xét tam giác vuông \(A'HE\) có: \(\tan \widehat {A'EH} = \dfrac{{A'H}}{{EH}} = \dfrac{{\dfrac{a}{2}}}{{\dfrac{{a\sqrt 3 }}{6}}} = \sqrt 3 \Rightarrow \widehat {A'EH} = {60^0}\) Chọn D. Câu hỏi 8 : Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng \(\varphi \,\,\left( {{0^0} < \varphi < {{90}^0}} \right)\). Tính tan của góc giữa hai mặt phẳng (SAB ) và (ABCD) theo \(\varphi \).
Đáp án: B Phương pháp giải: +) Xác định góc giữa cạnh bên và mặt đáy. +) Gọi E là trung điểm của AB, chứng minh \(\widehat {\left( {\left( {SAB} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SE;OE} \right)}\) Lời giải chi tiết:
Gọi O là tâm hình vuông ABCD. Vì chóp S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\) Ta có OB là hình chiếu của SB lên (ABCD) nên \(\widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;OB} \right)} = \widehat {SBO} = \varphi \,\,\left( {\widehat {SBO} < {{90}^0}} \right)\) Gọi E là trung điểm của AB Tam giác SAB cân tại S nên \(SE \bot AB\) \(\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SE \bot AB\\OE \bot AB\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SE;OE} \right)} = \widehat {SEO}\) (Vì \(\widehat {SEO} < {90^0}\) ) Ta có: \(OB = \frac{{a\sqrt 2 }}{2};OE = \dfrac{a}{2}\) Xét tam giác vuông SOB có: \(\tan \varphi = \dfrac{{SO}}{{OB}} \Rightarrow SO = \dfrac{{a\sqrt 2 }}{2}\tan \varphi \) Xét tam giác vuông SOE có: \(\tan \widehat {SEO} = \dfrac{{SO}}{{OE}} \Rightarrow SO = \dfrac{a}{2}.\tan \widehat {SEO}\) \( \Rightarrow \dfrac{{a\sqrt 2 }}{2}\tan \varphi = \frac{a}{2}\tan \widehat {SEO} \Rightarrow \tan \widehat {SEO} = \sqrt 2 \tan \varphi \) Chọn B. Câu hỏi 9 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của BC. Tan góc giữa (SAI) và (ABCD)?
Đáp án: B Phương pháp giải: +) Gọi H là trung điểm của AB. Chứng minh \(SH \bot \left( {ABCD} \right)\) +) Chứng minh \(AI \bot DH\) +) Chứng minh \(\widehat {\left( {\left( {SAI} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SE;DH} \right)}\) Lời giải chi tiết:
Gọi H là trung điểm của AB Vì tam giác SAB vuông cân tại S \( \Rightarrow SH \bot AB\) Ta có: \(\left. \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SH \bot AB\end{array} \right\} \Rightarrow SH \bot \left( {ABCD} \right)\) Dễ dàng chứng minh được \(AI \bot DH\) Ta có: \(\left. \begin{array}{l}AI \bot DH\\AI \bot SH\left( {SH \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AI \bot \left( {SHD} \right) \Rightarrow AI \bot SE\) \(\left. \begin{array}{l}\left( {SAI} \right) \cap \left( {ABCD} \right) = AI\\SE \bot AI\\DH \bot AI\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAI} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SE;DH} \right)} = \widehat {SEH}\) (Vì \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot HE \Rightarrow \Delta SHE\) vuông tại H \( \Rightarrow \widehat {SEH} < {90^0}\))
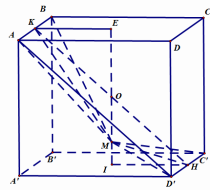
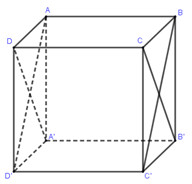
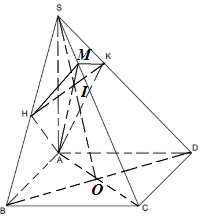
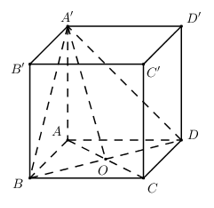
Xét tam giác vuông AHD có: \(HD = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2}\) \(HE.HD = A{H^2} \Rightarrow HE = \dfrac{{A{H^2}}}{{HD}} = \dfrac{{\dfrac{{{a^2}}}{4}}}{{\dfrac{{a\sqrt 5 }}{2}}} = a\dfrac{{\sqrt 5 }}{{10}}\) Xét tam giác vuông SAB có: \(SH = \dfrac{1}{2}AB = \dfrac{a}{2}\) Trong tam giác vuông SHE có: \(\tan \widehat {SEH} = \dfrac{{SH}}{{SE}} = \dfrac{{\dfrac{a}{2}}}{{\dfrac{{a\sqrt 5 }}{{10}}}} = \sqrt 5 \) Chọn B. Câu hỏi 10 : Cho hình lập phương \(ABCD.A'B'C'D'\) có tâm \(O\). Gọi \(I\) là tâm của hình vuông \(A'B'C'D'\) và \(M\) là điểm thuộc đoạn thẳng \(OI\) sao cho \(MO = 2MI\) (tham khảo hình vẽ). Khi đó côsin của góc tạo bởi hai mặt phẳng \(\left( {MC'D'} \right)\) và \(\left( {MAB} \right)\) bằng
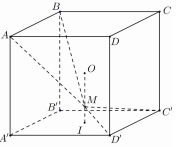
Đáp án: B Phương pháp giải: - Xác định góc giữa hai mặt phẳng \(\left( {MAB} \right),\left( {MC'D'} \right)\) chính là góc giữa hai đường thẳng cùng vuông góc giao tuyến. - Gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(M\) trên \(C'D',AB\) thì góc \(\varphi \) là góc giữa \(MH,MK\) - Sử dụng định lý hàm số cos để tính \(\widehat {HMK}\) và kết luận. Lời giải chi tiết:
Nhận thấy giao tuyến của hai mặt phẳng \(\left( {MAB} \right),\left( {MC'D'} \right)\) là đường thẳng đi qua \(M\) và song song với \(AB,C'D'\) Gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(M\) trên \(C'D',AB\) Khi đó \(\left( {\left( {MC'D'} \right),\left( {MAB} \right)} \right) = \left( {MH,MK} \right) = \varphi \Rightarrow \cos \varphi = \left| {\cos \widehat {HMK}} \right|\) Giả sử hình lập phương có cạnh bằng \(6\) Ta có: \(IM = 1,IH = 3 \Rightarrow MH = \sqrt {10} \) Gọi \(E\) là tâm hình vuông \(ABCD \Rightarrow EM = 5;EK = 3 \Rightarrow MK = \sqrt {34} \) Mà \(HK = AD' = 6\sqrt 2 \) Suy ra \(\cos \widehat {HMK} = \frac{{M{K^2} + M{H^2} - H{K^2}}}{{2MH.MK}} = - \frac{{7\sqrt {85} }}{{85}}\) Vậy \(\cos \varphi = \frac{{7\sqrt {85} }}{{85}}\) Chọn B. Câu hỏi 11 : Cho lăng trụ đều \(ABC.A'B'C'\) có cạnh đáy bằng a và cạnh bên là \(\frac{{3a}}{2}\). Tính số đo góc tạo bởi hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\).
Đáp án: A Phương pháp giải: Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\): - Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\). - Xác định 1 mặt phẳng \(\left( \gamma \right) \bot \Delta \). - Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right)\) - Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\): \(\left( {\widehat {\left( \alpha \right);\left( \beta \right)}} \right) = \left( {\widehat {a;b}} \right)\) Lời giải chi tiết:
Gọi M là trung điểm của BC. Khi đó, \(AM \bot BC\) (do \(\Delta ABC\) đều) Mà \(BC \bot AA' \Rightarrow BC \bot \left( {AMA'} \right)\) \( \Rightarrow \left( {\widehat {\left( {ABC} \right),\left( {A'BC} \right)}} \right) = \left( {\widehat {AM,\,A'M}} \right) = \widehat {AMA'}\) \(\Delta ABC\) đều, cạnh bằng a \( \Rightarrow AM = \frac{{a\sqrt 3 }}{2}\) \(\Delta AMA'\) vuông tại A \( \Rightarrow \tan \widehat {AMA'} = \frac{{AA'}}{{AM}} = \frac{{\frac{{3a}}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \sqrt 3 \Rightarrow \widehat {AMA'} = {60^0}\) \( \Rightarrow \left( {\widehat {\left( {ABC} \right),\left( {A'BC} \right)}} \right) = {60^0}\). Chọn: A Câu hỏi 12 : Cho lăng trụ đứng \(ABC.A'B'C'\) có \(AB = AC = BB' = a\), \(\widehat {BAC} = 120^\circ \). Gọi \(I\) là trung điểm của \(CC'\). Ta có cosin của góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'I} \right)\) bằng:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Diện tích tam giác \(ABC\): \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin \widehat A = \frac{{\sqrt 3 {a^2}}}{4}\). Có \(BC = \sqrt {A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC}} = a\sqrt 3 \). Ta có: \(AB' = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \), \(AI = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\), \(B'I = \sqrt {3{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {13} }}{2}\). Ta được \(A{B'^2} + A{I^2} = 2{a^2} + {\left( {\frac{{a\sqrt 5 }}{2}} \right)^2} = \frac{{13{a^2}}}{4} = B'{I^2}\). Suy ra tam giác \(AB'I\) vuông tại \(A\), có diện tích bằng: \({S_{AB'I}} = \frac{1}{2}.AB'.AI = \frac{1}{2}a\sqrt 2 \cdot \frac{{a\sqrt 5 }}{2} = \frac{{{a^2}\sqrt {10} }}{4}\). Tam giác \(ABC\) là hình chiếu vuông góc của tam giác \(AB'I\) trên \(\left( {ABC} \right)\) nên ta có: \({S_{ABC}} = \cos \alpha .{S_{AB'I}} \Leftrightarrow \cos \alpha = \frac{{{a^2}\sqrt 3 }}{4}:\frac{{{a^2}\sqrt {10} }}{4} = \frac{{\sqrt {30} }}{{10}}\). Chọn B Câu hỏi 13 : Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng (A’B’CD) và (ABC’D’) bằng:
Đáp án: D Phương pháp giải: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng thuộc hai mặt phẳng cùng vuông góc với giao tuyến chung của hai mặt phẳng. Lời giải chi tiết: Cách 1: Có thể giải theo phương pháp gắn hệ trục tọa độ. Cách 2: Tìm hai đường thẳng lần lượt vuông góc với hai mặt phẳng.
Ta có: \(\left\{ \begin{array}{l}AD' \bot A'D\\AD' \bot A'B'\end{array} \right. \Rightarrow AD' \bot \left( {A'B'CD} \right)\) Lại có: \(\left\{ \begin{array}{l}A'D \bot A'D'\\A'D \bot C'D'\end{array} \right. \Rightarrow A'D \bot \left( {ABC'D'} \right)\) Do đó góc giữa hai mp \(\left( {ABC'D'} \right)\) và \(\left( {A'B'CD} \right)\) bằng góc \(AD'\) và \(A'D\) Mà \(A'D \bot AD'\) Vậy góc cần tìm bằng \({90^0}\) CHỌN D. Câu hỏi 14 : Cho tứ diện ABCD có \(\left( {ACD} \right) \bot \left( {BCD} \right),\,\,AC = AD = BC = BD = a,\,\,CD = 2x\). Giá trị của x để hai mặt phẳng (ABC) và (ABD) vuông góc với nhau là :
Đáp án: B Phương pháp giải: +) Gọi E là trung điểm của AB, chứng minh \(\widehat {\left( {\left( {ABC} \right);\left( {ABD} \right)} \right)} = \widehat {\left( {CE;DE} \right)} = \widehat {CED}\). +) Sử dụng định lí Pytago trong các tam giác vuông tìm x. Lời giải chi tiết: Gọi H là trung điểm của CD. Do tam giác ACD cân tại A và tam giác BCD cân tại B \( \Rightarrow \left\{ \begin{array}{l}CD \bot AH\\CD \bot BH\end{array} \right. \Rightarrow CD \bot \left( {ABH} \right) \Rightarrow CD \bot AB\) Gọi E là trung điểm của AB, do tam giác ABC cân tại C \( \Rightarrow CE \bot AB\). Ta có \(\left\{ \begin{array}{l}AB \bot CD\\AB \bot CE\end{array} \right. \Rightarrow AB \bot \left( {CDE} \right) \Rightarrow AB \bot DE\) \(\left\{ \begin{array}{l}\left( {ABC} \right) \cap \left( {ABD} \right) = AB\\\left( {ABC} \right) \supset CE \bot AB\\\left( {ABD} \right) \supset DE \bot AB\end{array} \right. \Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABD} \right)} \right) = \angle \left( {CE;DE} \right) = \angle CED = {90^0}\) 
Ta có \(\Delta ABC = \Delta ADC\,\,\left( {c.c.c} \right) \Rightarrow CE = DE \Rightarrow \Delta CDE\) vuông cân tại E \( \Rightarrow CD = CE\sqrt 2 \Leftrightarrow 2x = CE\sqrt 2 \Leftrightarrow CE = x\sqrt 2 \) (*) Xét tam giác vuông CBH có \(B{H^2} = B{C^2} - C{H^2} = {a^2} - {x^2}\) Xét tam giác vuông ACH có \(A{H^2} = A{C^2} - C{H^2} = {a^2} - {x^2}\) Xét tam giác vuông ABH có \(A{B^2} = A{H^2} + B{H^2} = 2{a^2} - 2{x^2} \Rightarrow AE = \dfrac{{\sqrt {2{a^2} - 2{x^2}} }}{2}\) Xét tam giác vuông ACE có \(C{E^2} = A{C^2} - A{E^2} = {a^2} - \dfrac{{{a^2} - {x^2}}}{2} = \dfrac{{{a^2} + {x^2}}}{2} \Rightarrow CE = \dfrac{{\sqrt {{a^2} + {x^2}} }}{{\sqrt 2 }}\) Thay vào (*) ta có \(\dfrac{{\sqrt {{a^2} + {x^2}} }}{{\sqrt 2 }} = x\sqrt 2 \Leftrightarrow {a^2} + {x^2} = 4{x^2} \Leftrightarrow 3{x^2} = {a^2} \Leftrightarrow x = \dfrac{{a\sqrt 3 }}{3}\). Chọn B.
Câu hỏi 15 : Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng \(a.\) Tính cosin của góc giữa hai mặt bên không liền kề nhau.
Đáp án: A Phương pháp giải: + Sử dụng định nghĩa để tìm góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) : \(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\a \bot d;\,a \subset \left( P \right)\\b \bot d;b \subset \left( Q \right)\end{array} \right.\) khi đó góc giữa \(\left( P \right)\) và \(\left( Q \right)\) chính là góc giữa hai đường thẳng \(a\) và \(b.\) + Sử dụng định lý hàm số cos trong tam giác để tính toán: Cho tam giác \(ABC\) khi đó \(\cos A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}}\) Lời giải chi tiết:
Hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng \(a\) , ta tìm góc giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\). Gọi \(M\), \(N\) là trung điểm các cạnh \(AD\) và \(BC\), khi đó \(SM \bot AD\) và \(SN \bot BC\) (do các tam giác \(SBC;SAD\) là các tam giác đều). Vì \(BC//AD\) nên giao tuyến của hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) là đường thẳng \(d\) qua \(S\) và song song \(AD\), \(BC\). Vì \(SM \bot AD\) và \(SN \bot BC\) nên \(S\) và \(D\) mà \(SM \subset \left( {SAD} \right);SN \subset \left( {SBC} \right)\) nên góc giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) là góc \(\widehat {MSN}\). Mặt bên là các tam giác đều cạnh \(a\) nên \(SM = SN = \dfrac{{a\sqrt 3 }}{2}\), \(MN = AB = a\). Khi đó : \(\cos \widehat {MSN} = \dfrac{{S{M^2} + S{N^2} - M{N^2}}}{{2SM.SN}} = \dfrac{{{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {a^2}}}{{2.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{\dfrac{{{a^2}}}{2}}}{{\dfrac{{3{a^2}}}{2}}} = \dfrac{1}{3}\). Chọn: A Câu hỏi 16 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại\(A\) và \(D\), \(AD = DC = a\). Biết \(SAB\) là tam giác đều cạnh \(2a\) và mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Tính cô sin của góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBC} \right)\).
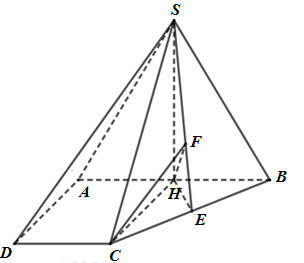
Đáp án: A Phương pháp giải: - Xác định góc giữa hai mặt phẳng (góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng) - Tính cô sin góc vừa xác định, sử dụng định lý hàm số cos. Lời giải chi tiết:
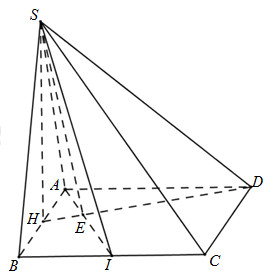
Gọi \(H,E\) lần lượt là trung điểm của \(AB,BC\). Kẻ \(HF \bot SE\). Do \(\Delta SAB\) đều và nằm trong mặt phẳng vuông góc với đáy nên \(SH \bot \left( {ABCD} \right)\). Do \(AB = 2a,AD = DC = a,\widehat A = \widehat D = {90^0}\) nên \(CH = HB = a,CH \bot AB,HE \bot BC\). Ta có: \(\left\{ \begin{array}{l}CH \bot AB\\CH \bot SH\end{array} \right. \Rightarrow CH \bot \left( {SAB} \right)\) Lại có \(BC \bot HE,BC \bot SH \Rightarrow BC \bot \left( {SHE} \right) \Rightarrow BC \bot HF\) Mà \(HF \bot SE\) nên \(HF \bot \left( {SBC} \right)\) Do đó góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBC} \right)\) là \(\widehat {\left( {HC,HF} \right)} = \widehat {FHC}\) (vì \(\widehat {FHC} < \widehat {HFC} = {90^0}\)) Xét tam giác \(SAB\) đều cạnh \(2a\) nên \(SH = \dfrac{{2a.\sqrt 3 }}{2} = a\sqrt 3 \). Tam giác \(HBC\) vuông cân tại \(H\), có \(HB = HC = a\) nên \(HE = \dfrac{{a\sqrt 2 }}{2}\). Xét tam giác \(\Delta SHE\) vuông tại \(H\) có \(HF\) là đường cao nên \(\dfrac{1}{{H{F^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{E^2}}} \Rightarrow HF = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {3{a^2} + \dfrac{{{a^2}}}{2}} }} = \dfrac{{a\sqrt {21} }}{7}\) Tam giác \(HFC\) vuông tại \(F\) có \(HF = \dfrac{{a\sqrt {21} }}{7},HC = a\) nên \(\cos \widehat {FHC} = \dfrac{{HF}}{{HC}} = \dfrac{{a\sqrt {21} }}{7}:a = \dfrac{{\sqrt {21} }}{7}\). Vậy cô sin của góc hợp bởi hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAB} \right)\) là \(\dfrac{{\sqrt {21} }}{7}\). Chọn A. Câu hỏi 17 : Cho khối chóp tứ giác đều \(S.ABCD\) có thể tích bằng \({a^3}\) và đáy \(ABCD\) là hình vuông cạnh \(a.\) Tính \(\cos \alpha \) với \(\alpha \) là góc giữa mặt bên và mặt đáy.
Đáp án: C Phương pháp giải: Thể tích của khối chóp ngoại tiếp hình chóp \(V = \frac{1}{3}Sh\). Lời giải chi tiết: Gọi O là tâm của hình vuông ABCD, I là trung điểm của BC. Ta có: \({V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SO = \frac{1}{3}.{a^2}.SO = {a^3} \Rightarrow SO = 3a\) Do \(\left\{ \begin{array}{l}OI \bot BC\\SI \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SOI} \right)\) Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\BC \bot \left( {SOI} \right)\\\left( {SOI} \right) \cap \left( {SBC} \right) = SI\\\left( {SOI} \right) \cap \left( {ABCD} \right) = OI\end{array} \right.\) \(\begin{array}{l} \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {OI;SI} \right) = \angle SIO\\ \Rightarrow \cos \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \cos \angle SIO = \frac{{OI}}{{SI}} = \frac{{OI}}{{\sqrt {O{I^2} + S{O^2}} }} = \frac{{\frac{a}{2}}}{{\sqrt {\frac{{{a^2}}}{4} + 9{a^2}} }} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt {37} }}{2}}} = \frac{1}{{\sqrt {37} }}.\end{array}\) Chọn C. Câu hỏi 18 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SAB\) là tam giác đều và \(\left( {SAB} \right)\) vuông góc với \(\left( {ABCD} \right).\) Tính \(\cos \varphi \) với \(\varphi \) là góc tạo bởi \((SAC)\) và \((SCD).\)
Đáp án: D Phương pháp giải: * Sử dụng cách tìm góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) như sau: + Xác định giao tuyến \(d\) của \(\left( P \right)\) và \(\left( Q \right)\) + Xác định mặt phẳng \(\left( R \right)\) vuông góc với đường thẳng \(d\). + Xác định giao tuyến \(a = \left( P \right) \cap \left( R \right);\,b = \left( Q \right) \cap \left( R \right)\) + Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) là góc giữa hai đường thẳng \(a\) và \(b\). * Tính toán bằng cách sử dụng định lý Pytago, tam giác đồng dạng, định lý hàm số cos trong tam giác. Cho tam giác \(MNQ\) thì \(\cos M = \dfrac{{M{N^2} + M{Q^2} - N{Q^2}}}{{2MN.MQ}}\) Lời giải chi tiết:
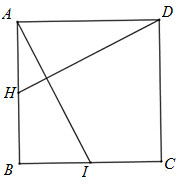
Gọi \(H;M\) là trung điểm của \(AB;BC\). \(DM\) cắt \(CH;AC\) lần lượt tại \(K\) và \(I\) . + Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right.\) mà \(SH \bot AB\) (do tam giác \(SAB\) đều có \(SH\) là đường trung tuyến) Suy ra \(SH \bot \left( {ABCD} \right)\) + Xét \(\Delta BHC = \Delta CMD\left( {c - g - c} \right) \Rightarrow \widehat B = \widehat {DMC}\) mà \(\widehat B + \widehat {BCH} = 90^\circ \Rightarrow \widehat {KMC} + \widehat {KCM} = 90^\circ \) \( \Rightarrow \widehat {MKC} = 90^\circ \Rightarrow MD \bot CH\) Ta có \(MD \bot CH\,\left( {cmt} \right);\,MD \bot SH\) (do \(SH \bot \left( {ABCD} \right)\)) nên \(MD \bot \left( {SHC} \right) \Rightarrow MD \bot SC\) + Trong \(\left( {SHC} \right)\) kẻ \(KE \bot SC\) tại \(E.\) Ta có \(KE \bot SC\) và \(MD \bot SC \Rightarrow SC \bot \left( {EKD} \right)\) Lại có \(\left\{ \begin{array}{l}\left( {SDC} \right) \bot \left( {KED} \right)\\\left( {SAC} \right) \bot \left( {KED} \right)\\\left( {SDC} \right) \cap \left( {KED} \right) = DE\\\left( {SAC} \right) \cap \left( {KED} \right) = IE\end{array} \right. \Rightarrow \) góc giữa \((SAC)\) và \((SCD)\) là góc tạo bởi \(EI;ED\). + Vì \(MC//AD \Rightarrow \dfrac{{IA}}{{IC}} = \dfrac{{ID}}{{IM}} = \dfrac{{AD}}{{MC}} = \dfrac{{2a}}{a} = 2\) \( \Rightarrow ID = \dfrac{2}{3}MD = \dfrac{2}{3}\sqrt {D{C^2} + M{C^2}} = \dfrac{2}{3}\sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{2}{3}.\dfrac{{a\sqrt 5 }}{2} = \dfrac{{a\sqrt 5 }}{3}\) Và \(\dfrac{{IA}}{{IC}} = 2 \Rightarrow IC = \dfrac{1}{3}AC = \dfrac{{a\sqrt 2 }}{2}\) + Xét tam giác vuông \(DMC\) có \(CK\) là đường cao nên \(CK.MD = MC.CD \Leftrightarrow CK.\dfrac{{a\sqrt 5 }}{2} = a.\dfrac{a}{2} \Rightarrow CK = \dfrac{a}{{\sqrt 5 }}\) + Ta có \(\Delta CEK\) đồng dạng với \(\Delta CHS\) \( \Rightarrow \dfrac{{EK}}{{SH}} = \dfrac{{CK}}{{CS}}\) \( \Rightarrow EK = \dfrac{{SH.CK}}{{CS}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{a}{{\sqrt 5 }}}}{{\sqrt {H{S^2} + C{H^2}} }} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{{2\sqrt 5 }}}}{{a\sqrt 2 }} = \dfrac{{a\sqrt 3 }}{{2\sqrt {10} }}\) + Tam giác \(KEC\) vuông tại E nên \(EC = \sqrt {C{K^2} - E{K^2}} = \sqrt {{{\left( {\dfrac{a}{{\sqrt 5 }}} \right)}^2} - {{\left( {\dfrac{{a\sqrt 3 }}{{2\sqrt {10} }}} \right)}^2}} = \dfrac{a}{{2\sqrt 2 }}\) + Tam giác \(IKC\) vuông tại K nên \(KI = \sqrt {I{C^2} - C{K^2}} = \sqrt {\dfrac{{2{a^2}}}{9} - \dfrac{{{a^2}}}{5}} = \dfrac{a}{{3\sqrt 5 }}\) + Xét tam giác \(EKI\) vuông tại K (vì \(MD \bot \left( {SHC} \right) \Rightarrow DK \bot KE\) ) có \(EI = \sqrt {E{K^2} + K{I^2}} = \sqrt {\dfrac{{3{a^2}}}{{40}} + \dfrac{{{a^2}}}{{45}}} = \dfrac{{a\sqrt 7 }}{{6\sqrt 2 }}\) + Xét tam giác \(ECD\) vuông tại E (do \(SC \bot \left( {EDK} \right) \Rightarrow SC \bot ED\)) có \(ED = \sqrt {C{D^2} - E{C^2}} = \sqrt {{a^2} - {{\left( {\dfrac{a}{{2\sqrt 2 }}} \right)}^2}} = \dfrac{{a\sqrt 7 }}{{2\sqrt 2 }}\) + Xét tam giác \(EID\) ta có \(\cos IED = \dfrac{{I{E^2} + E{D^2} - I{D^2}}}{{2IE.ED}} = \dfrac{{\dfrac{{7{a^2}}}{{72}} + \dfrac{{7{a^2}}}{8} - \dfrac{{5{a^2}}}{9}}}{{2.\dfrac{{a\sqrt 7 }}{{6\sqrt 2 }}.\dfrac{{a\sqrt 7 }}{{2\sqrt 2 }}}} = \dfrac{5}{7} > 0\) Vậy \(\cos \varphi = \dfrac{5}{7}.\) Chọn D. Câu hỏi 19 : Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng AA’, BB’, CC’ thỏa mãn diện tích của tam giác MNP bằng \({a^2}.\) Góc giữa hai mặt phẳng (MNP) và (ABCD) là
Đáp án: A Phương pháp giải: Sử dụng công thức \({S_{\Delta ABC}} = {S_{\Delta MNB}}.\cos \alpha \) với \(\alpha = \angle \left( {\left( {MNP} \right);\left( {ABCD} \right)} \right)\). Lời giải chi tiết: Ta có hình chiếu của tam giác \(MNP\) lên \(\left( {ABCD} \right)\) chính là tam giác \(ABC\) Gọi \(\alpha = \angle \left( {\left( {MNP} \right);\left( {ABCD} \right)} \right)\) \( \Rightarrow {S_{\Delta ABC}} = {S_{\Delta MNB}}.\cos \alpha \Rightarrow \frac{{{a^2}}}{2} = {a^2}\cos \alpha \Rightarrow \cos \alpha = \frac{1}{2} \Rightarrow \alpha = {60^0}\) Chọn A. Câu hỏi 20 : Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(BC = a,\,\,BB' = a\sqrt 3 \). Góc giữa hai mặt phẳng \(\left( {A'B'C} \right)\) và \(\left( {ABC'D'} \right)\) bằng :
Đáp án: C Phương pháp giải: Góc giữa 2 mặt phẳng là góc giữa 2 đường thẳng lần lượt thuộc 2 mặt phẳng và vuông góc với giao tuyến của 2 mặt phẳng đó. Lời giải chi tiết:
Ta có: \(\left( {A'B'C} \right) \equiv \left( {A'B'CD} \right) \Rightarrow \angle \left( {\left( {A'B'C} \right);\left( {ABC'D'} \right)} \right) = \angle \left( {\left( {A'B'CD} \right);\left( {ABC'D'} \right)} \right)\) Gọi \(O = AD \cap A'D,\,\,O' = BC' \cap B'C \Rightarrow \left( {A'B'CD} \right) \cap \left( {ABC'D'} \right) = OO'\). Ta có \(ADD'A'\) và \(BCC'B'\) là các hình chữ nhật \( \Rightarrow O\) là trung điểm của \(AD',\,\,A'D\). \(O'\) là trung điểm của \(B'C,\,\,BC'\). Ta có \(\left\{ \begin{array}{l}AB//C'D'\\AB = C'D'\end{array} \right. \Rightarrow ABC'D'\) là hình bình hành. Lại có \(AB \bot \left( {BCC'D'} \right) \Rightarrow AB \bot BC' \Rightarrow ABC'D'\) là hình chữ nhật \( \Rightarrow OO' \bot AD'\). Hoàn toàn tương tự ra chứng minh được \(OO' \bot A'D\). Ta có \(\left\{ \begin{array}{l}\left( {ABC'D'} \right) \cap \left( {A'B'CD} \right) = OO'\\\left( {ABC'D'} \right) \supset AD' \bot OO'\\\left( {A'B'CD} \right) \supset A'D \bot OO'\end{array} \right. \Rightarrow \angle \left( {\left( {A'B'CD} \right);\left( {ABC'D'} \right)} \right) = \angle \left( {AD';A'D} \right)\). Ta có : \(OA = \dfrac{1}{2}A'D = \dfrac{1}{2}\sqrt {A{D^2} + AA{'^2}} = \dfrac{1}{2}\sqrt {{a^2} + 3{a^2}} = a = OD \Rightarrow \Delta OAD\) đều \( \Rightarrow \angle AOD = {60^0}\) . Vậy \(\angle \left( {AD';A'D} \right) = \angle AOD = {60^0}\). Chọn C. Câu hỏi 21 : Cho hình chóp \(S.ABCD\) có tất cả các cạnh đều bằng \(a\). Tan của góc giữa mặt bên và mặt đáy bằng :
Đáp án: A Phương pháp giải: +) Xác định góc giữa mặt bên và đáy là góc giữa hai đường thẳng lần lượt thuộc 2 mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng đó. +) Tính tan của góc xác định được. Lời giải chi tiết:
Gọi \(O = AC \cap BD\). Do \(S.ABCD\) là chóp đều \( \Rightarrow SO \bot \left( {ABCD} \right)\). Gọi \(M\) là trung điểm của \(CD\) ta có: \(OM\) là đường trung bình của tam giác \(BCD \Rightarrow OM//BC\). \( \Rightarrow OM \bot CD\). Ta có: \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right) \Rightarrow CD \bot SM\). \(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {SCD} \right) \supset SM \bot CD\\\left( {ABCD} \right) \supset OM \bot CD\end{array} \right. \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right) = \angle SMO\). Ta có \(OM = \dfrac{a}{2}\). \(\Delta SCD\) đều cạnh \(a \Rightarrow SM = \dfrac{{a\sqrt 3 }}{2}\). Áp dụng định lí Pytago trong tam giác vuông \(SOM\) ta có: \(SO = \sqrt {S{M^2} - O{M^2}} = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 2 }}{2}\). \( \Rightarrow \tan \angle SMO = \dfrac{{SO}}{{OM}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}}}{{\dfrac{a}{2}}} = \sqrt 2 \). Chọn A. Câu hỏi 22 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(2a\), \(SA = SB = SC = SD = 2a\). Gọi \(\varphi \) là góc giữa mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\). Mệnh đề nào dưới đây là đúng ?
Đáp án: D Phương pháp giải: +) Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\). +) Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến. Xác định góc giữa \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\). +) Tính tan của góc xác định được. Lời giải chi tiết:
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\). Gọi \(M\) là trung điểm của \(CD\) ta có \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right) \Rightarrow CD \bot SM\). \(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {SCD} \right) \supset SM \bot CD\\\left( {ABCD} \right) \supset OM \bot CD\end{array} \right. \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right) = \angle SMO = \gamma \). Ta có \(OM = \dfrac{1}{2}AD = \dfrac{1}{2}.2a = a\). Tam giác \(SCD\) đều cạnh \(2a \Rightarrow SM = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \). \( \Rightarrow SO = \sqrt {S{M^2} - S{O^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \) (Định lí Pytago) \( \Rightarrow \tan \gamma = \tan \angle SMO = \dfrac{{SO}}{{OM}} = \dfrac{{a\sqrt 2 }}{a} = \sqrt 2 \). Chọn D. Câu hỏi 23 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = AD\sqrt 2 \), \(SA \bot \left( {ABC} \right)\). Gọi \(M\) là trung điểm của \(AB\). Góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SDM} \right)\) bằng
Đáp án: B Phương pháp giải: Chứng minh hai mặt phẳng đã cho vuông góc để suy ra góc giữa hai mặt phẳng. Để chứng minh \(\left( P \right) \bot \left( Q \right)\) ta chứng minh \(d \bot \left( Q \right)\) mà \(d \subset \left( P \right).\) Lời giải chi tiết:
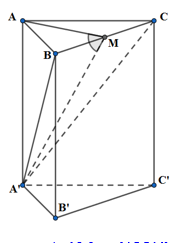
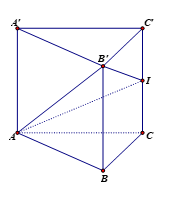
Gọi \(K\) là giao điểm của \(AC\) và \(DM\). Ta có \(AM = MB = \dfrac{{AB}}{2} = \dfrac{{AD\sqrt 2 }}{2}\) và \(BC = AD\) Xét tam giác vuông \(ADM\) có \(\tan \widehat {ADM} = \dfrac{{AM}}{{AD}} = \dfrac{{\dfrac{{AD\sqrt 2 }}{2}}}{{AD}} = \dfrac{{\sqrt 2 }}{2}\) (1) Xét tam giác vuông \(ABC\) có \(\tan \widehat {BAC} = \dfrac{{BC}}{{AB}} = \dfrac{{AD}}{{AD\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}\) (2) Từ (1) và (2) suy ra \(\tan \widehat {ADM} = \tan \widehat {BAC} \Rightarrow \widehat {ADM} = \widehat {BAC}\) mà \(\widehat {ADM} + \widehat {AMD} = 90^\circ \Rightarrow \widehat {BAC} + \widehat {AMK} = 90^\circ \Rightarrow \widehat {AKM} = 90^\circ \) hay \(DM \bot AC\) (3) Lại có \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC\) (4) Từ (3) và (4) suy ra \(AC \bot \left( {SDM} \right) \Rightarrow \left( {SAC} \right) \bot \left( {SDM} \right)\) nên góc giữa \(\left( {SAC} \right)\) và \(\left( {SDM} \right)\) bằng \(90^\circ .\) Chọn B. Câu hỏi 24 : Cho lăng trụ đều \(ABC.A'B'C'\) có \(AB = 2\sqrt 3 ,\,\,BB' = 2\).Gọi \(M,\,\,N,\,\,P\) tương ứng là trung điểm của \(A'B',\,\,A'C',\,\,BC\). Nếu gọi \(\alpha \) là độ lớn của góc của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {ACC'} \right)\) thì \(\cos \alpha \)bằng:
Đáp án: B Phương pháp giải: Sử dụng định lí hình chiếu : \(S' = S.\cos \varphi \Rightarrow \) \(\cos \varphi = \dfrac{{S'}}{S}\) . Lời giải chi tiết: Ta có: \(\left( {MNP} \right) \equiv \left( {MNCP} \right)\) (do \(CP//B'C'//MN\)) và \(\left( {ACC'} \right) \equiv \left( {ACC'A'} \right)\) \( \Rightarrow \alpha = \widehat {\left( {\left( {MNP} \right);\left( {ACC'} \right)} \right)} = \widehat {\left( {\left( {MNCP} \right);\left( {ACC'A'} \right)} \right)}\) Dựng \(PE \bot AC,\,\,MF \bot A'C',\,\,\left( {E \in AC;\,F \in A'C'} \right)\) \( \Rightarrow CE = FN = \dfrac{1}{4}AC\) và \(P,E,F,M\) đồng phẳng Ta có: \(PE \bot AC,\,\,PE \bot AA' \Rightarrow PE \bot \left( {ACC'A'} \right) \Rightarrow \left( {PEFM} \right) \bot \left( {ACC'A'} \right)\) \( \Rightarrow \) Hình chiếu vuông góc của hình bình hành lên \(\left( {ACC'A'} \right)\) là hình bình hành \(ECNF\)\( \Rightarrow \cos \alpha = \dfrac{{{S_{ECNF}}}}{{{S_{MNCP}}}}\) Ta có: \({S_{ECNF}} = EC.CC' = \dfrac{1}{4}.AC.CC' = \dfrac{1}{4}.2\sqrt 3 .2 = \sqrt 3 \); \(\Delta A'B'C'\) đều \( \Rightarrow C'M = 2\sqrt 3 .\dfrac{{\sqrt 3 }}{2} = 3\) \(\Delta CC'M\) vuông tại C’ \( \Rightarrow CM = \sqrt {CC{'^2} + C'{M^2}} = \sqrt {{2^2} + {3^2}} = \sqrt {13} \)
\(\Delta CC'N\) vuông tại C’ \( \Rightarrow CN = \sqrt {CC{'^2} + C'{N^2}} = \sqrt {{2^2} + {{\sqrt 3 }^2}} = \sqrt 7 \) \(\Delta MNC\) có: \(MN = \sqrt 3 ,\,\,CM = \sqrt {13} ,\,\,CN = \sqrt 7 \), có diện tích là: \({S_{MNC}} = \sqrt {p.\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) \( = \sqrt {\dfrac{{\sqrt 3 + \sqrt 7 + \sqrt {13} }}{2}.\left( {\dfrac{{\sqrt 3 + \sqrt 7 + \sqrt {13} }}{2} - \sqrt 3 } \right)\left( {\dfrac{{\sqrt 3 + \sqrt 7 + \sqrt {13} }}{2} - \sqrt 7 } \right)\left( {\dfrac{{\sqrt 3 + \sqrt 7 + \sqrt {13} }}{2} - \sqrt {13} } \right)} \) \( = \sqrt {\dfrac{{\sqrt 3 + \sqrt 7 + \sqrt {13} }}{2}.\dfrac{{\sqrt 7 + \sqrt {13} - \sqrt 3 }}{2}.\dfrac{{\sqrt 3 + \sqrt {13} - \sqrt 7 }}{2}.\dfrac{{\sqrt 3 + \sqrt 7 - \sqrt {13} }}{2}} = \dfrac{{5\sqrt 3 }}{4}\) \( \Rightarrow {S_{MNCP}} = \dfrac{{5\sqrt 3 }}{2}\) \( \Rightarrow \cos \alpha = \dfrac{{{S_{ECNF}}}}{{{S_{MNCP}}}} = \dfrac{{\sqrt 3 }}{{\dfrac{{5\sqrt 3 }}{2}}} = \dfrac{2}{5}\). Chọn: B Câu hỏi 25 : Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(2\)và cạnh bên bằng \(2\sqrt 2 \). Gọi \(\alpha \)là góc của mặt phẳng \(\left( {SAC} \right)\) và mặt phẳng \(\left( {SAB} \right)\). Khi đó \(\cos \alpha \) bằng:
Đáp án: C Phương pháp giải: Sử dụng định lí hình chiếu : \(S' = S.\cos \varphi \Rightarrow \) \(\cos \varphi = \dfrac{{S'}}{S}\) . Lời giải chi tiết:
Gọi O là tâm của hình vuông ABCD. Do \(\left\{ \begin{array}{l}OB \bot AC\\OB \bot SO\end{array} \right. \Rightarrow OB \bot \left( {SAC} \right) \Rightarrow \) Hình chiếu vuông góc của tam giác SAB lên (SAC) là tam giác SAO Khi đó, \(\cos \alpha = \cos \left( {\widehat {\left( {SAB} \right);\left( {SAC} \right)}} \right) = \dfrac{{{S_{SAO}}}}{{{S_{SAB}}}}\) Ta có: \(\Delta SOA\) vuông tại O :
\({S_{SAB}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) \( = \sqrt {\dfrac{{2 + 2\sqrt 2 + 2\sqrt 2 }}{2}.\left( {\dfrac{{2 + 2\sqrt 2 + 2\sqrt 2 }}{2} - 2} \right)\left( {\dfrac{{2 + 2\sqrt 2 + 2\sqrt 2 }}{2} - 2\sqrt 2 } \right)\left( {\dfrac{{2 + 2\sqrt 2 + 2\sqrt 2 }}{2} - 2\sqrt 2 } \right)} \) \( = \sqrt {\left( {1 + 2\sqrt 2 } \right).\left( {2\sqrt 2 - 1} \right).1.1} = \sqrt 7 \) \( \Rightarrow \cos \alpha = \dfrac{{{S_{SAO}}}}{{{S_{SAB}}}} = \dfrac{{\sqrt 3 }}{{\sqrt 7 }} = \dfrac{{\sqrt {21} }}{7}\). Chọn: C Câu hỏi 26 : Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với mặt phẳng (ABCD). Gọi H, K lần lượt là hình chiếu vuông góc của A lên các đường thẳng SB và SD. Biết \(\angle HAK = 40^0.\) Góc giữa hai mặt phẳng (SBC) và (SCD) bằng
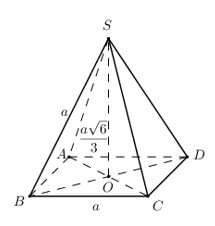
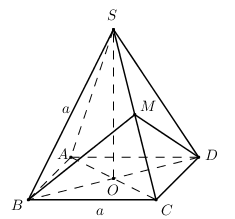
Đáp án: A Phương pháp giải: +) Xác định thiết diện của hình chóp cắt bởi \(\left( {AHK} \right)\). +) Xác định góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\). +) Chứng minh \(SC \bot \left( {AHK} \right)\). +) Xác định 2 góc còn lại của thiết diện của hình chóp cắt bởi \(\left( {AHK} \right)\). Lời giải chi tiết: Gọi \(O = AC \cap BD\), trong \(\left( {SBD} \right)\) gọi \(I = HK \cap SO\), trong \(\left( {SAC} \right)\) gọi \(M = AI \cap SC\). Khi đó ta có \(\left( {AHK} \right) \equiv \left( {AHMK} \right)\). Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\\\left\{ \begin{array}{l}AH \bot BC\\AH \bot SB\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\end{array}\). Hoàn toàn tương tự ta chứng minh được \(AK \bot SC \Rightarrow SC \bot \left( {AHMK} \right) \Rightarrow \left\{ \begin{array}{l}SC \bot HM\\SC \bot KM\end{array} \right.\) \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {SCD} \right) = SC\\\left( {SBC} \right) \supset HM \bot SC\\\left( {SCD} \right) \supset KM \bot SC\end{array} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = \angle \left( {HM;KM} \right) = \angle HMK\) Ta có: \(AH \bot \left( {SBC} \right) \Rightarrow AH \bot HM \Rightarrow \angle AHM = {90^0}\). Tương tự ta có \(\angle AKM = {90^0}\). Xét tứ giác \(AHMK\) có : \(\angle HAK + \angle AHM + \angle AKM + \angle HMK = {360^0} \Leftrightarrow \angle HMK = {360^0} - {40^0} - {90^0} - {90^0} = {140^0} > {90^0}\). Vậy \(\angle \left( {HM;KM} \right) = {180^0} - {140^0} = {40^0} \Rightarrow \angle \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = {40^0}\). Chọn A. Câu hỏi 27 : Cho hình chóp \(S.ABCD\) đáy là hình thoi tâm \(O\) và \(SO \bot \left( {ABCD} \right)\), \(SO = \dfrac{{a\sqrt 6 }}{3},\,\,BC = SB = a\). Số đo góc giữa 2 mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) là:
Đáp án: A Phương pháp giải: +) Gọi \(M\) là trung điểm của \(SC\). Chứng minh \(\angle \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = \angle \left( {BM;DM} \right)\). +) Tính các cạnh \(BM,\,\,DM,\,\,BD\) và sử dụng định lí cosin trong tam giác \(BDM\). Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(SC\). Tam giác \(SBC\) cân tại \(B \Rightarrow BM \bot SC\). Xét tam giác \(SBD\) có \(SO\) là trung tuyến đồng thời là đường cao \( \Rightarrow \Delta SBC\) cân tại \(S \Rightarrow SB = SD = a\). \(\Delta SCD\) có \(SD = CD = a \Rightarrow \Delta SCD\) cân tại \(D \Rightarrow DM \bot SC\). Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {SCD} \right) = SC\\\left( {SBC} \right) \supset BM \bot SC\\\left( {SCD} \right) \supset DM \bot SC\end{array} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = \angle \left( {BM;DM} \right)\). Xét chóp \(B.SAC\) ta có \(BC = BS = BA = a \Rightarrow \) Hình chiếu của \(B\) lên \(\left( {SAC} \right)\) trùng với tâm đường tròn ngoại tiếp \(\Delta SAC\). Ta có \(\left\{ \begin{array}{l}BO \bot AC\,\,\left( {gt} \right)\\BO \bot SO\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow BO \bot \left( {SAC} \right) \Rightarrow O\) là tâm đường tròn ngoại tiếp \(\Delta SAC\). \( \Rightarrow \Delta SAC\) vuông cân tại \(S \Rightarrow AC = 2SO = \dfrac{{2a\sqrt 6 }}{3} \Rightarrow SA = SC = \dfrac{{AC}}{{\sqrt 2 }} = \dfrac{{2a\sqrt 3 }}{3}\). Xét tam giác vuông \(OAB\) có \(OB = \sqrt {A{B^2} - O{A^2}} = \sqrt {{a^2} - \dfrac{{2{a^2}}}{3}} = \dfrac{{a\sqrt 3 }}{3}\)\( \Rightarrow BD = 2OB = \dfrac{{2a\sqrt 3 }}{3}\). Xét tam giác vuông \(BCM:\,\,BM = \sqrt {B{C^2} - M{C^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt 6 }}{3} = DM\). Áp dụng định lí Cosin trong tam giác \(BDM\) ta có: \(\cos \angle BMD = \dfrac{{B{M^2} + D{M^2} - B{D^2}}}{{2BM.DM}} = \dfrac{{\dfrac{{2{a^2}}}{3} + \dfrac{{2{a^2}}}{3} - \dfrac{{4{a^2}}}{3}}}{{2.\dfrac{{2{a^2}}}{3}}} = 0 \Rightarrow \angle BMD = {90^0}\). Vậy \(\angle \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = {90^0}\). Chọn A. Câu hỏi 28 : Cho tứ diện \(ABCD\) có \(AC = AD = BC = BD = a,\,\,\left( {ACD} \right) \bot \left( {BCD} \right)\) và \(\left( {ABC} \right) \bot \left( {ABD} \right)\). Tính độ dài cạnh \(CD\).
Đáp án: A Phương pháp giải: +) Gọi \(M,N\) lần lượt là trung điểm của \(CD,AB\). Chứng minh \(\Delta CDN\) và \(ABM\) vuông cân và \(MN \bot AB,\,\,\,MN \bot CD\). +) Đặt \(CD=x.\) Áp dụng định lí Pytago tính \(x\). Lời giải chi tiết:
Gọi \(M,N\) lần lượt là trung điểm của \(CD,AB\). \(\Delta ACD\) và \(\Delta BCD\) cân \( \Rightarrow AM \bot CD,\,\,BM \bot CD\). Ta có : \(\left\{ \begin{array}{l} \( \Rightarrow AM \bot BM\) Và ta dễ dàng chứng minh được \(\Delta ACD=\Delta BC\,\,\left( c.c.c \right)\Rightarrow AM=BM\).
\( \Rightarrow \Delta ABM\) vuông cân tại \(M\Rightarrow MN\bot AB\). Chứng minh tương tự ta có \(\Delta CDN\) vuông cân tại \(N\) và \(MN\bot CD\). Đặt \(CD=x\). Áp dụng định lí Pytago ta có: \(A{M^2} = {a^2} - \dfrac{{{x^2}}}{4}\). \(\Delta ABM\) vuông cân tại \(M\Rightarrow A{{B}^{2}}=2A{{M}^{2}}=2{{a}^{2}}-\dfrac{{{x}^{2}}}{2}\Rightarrow A{{N}^{2}}=\dfrac{1}{4}A{{B}^{2}}=\dfrac{{{a}^{2}}}{2}-\dfrac{{{x}^{2}}}{8}\). Áp dụng định lí Pytago ta có: \(D{{N}^{2}}=A{{D}^{2}}-A{{N}^{2}}={{a}^{2}}-\dfrac{{{a}^{2}}}{2}+\dfrac{{{x}^{2}}}{8}=\dfrac{{{a}^{2}}}{2}+\dfrac{{{x}^{2}}}{8}\) \(\Delta CDN\) vuông cân tại \(N\Rightarrow C{{D}^{2}}=2D{{N}^{2}}={{a}^{2}}+\dfrac{{{x}^{2}}}{4}={{x}^{2}}\Leftrightarrow x=\dfrac{2\sqrt{3}a}{3}\) Chọn A. Câu hỏi 29 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B,\,\,AB = BC = a\) và \(SA \bot \left( {ABC} \right)\). Góc giữa \(SC\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({45^0}\). Tính \(SA\) .
Đáp án: A Phương pháp giải: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó. Lời giải chi tiết:
Tam giác \(ABC\) cân tại \(B\) có \(AB = BC = a \Rightarrow AC = a\sqrt 2 \). Vì \(SA \bot \left( {ABC} \right) \Rightarrow AC\) là hình chiếu của \(SC\) lên \(\left( {ABC} \right)\). \( \Rightarrow \angle \left( {SC;\left( {ABC} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA = {45^0}\) \( \Rightarrow \Delta SAC\) vuông cân tại \(A \Rightarrow SA = AC = a\sqrt 2 \). Chọn A. Câu hỏi 30 : Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\) và đáy \(ABC\) là tam giác vuông tại \(B\). Hãy chọn khẳng định sai?
Đáp án: B Phương pháp giải: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\). Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\). Mà \(BC \subset \left( {ABC} \right);\,\,BC \subset \left( {SBC} \right) \Rightarrow \left( {SAB} \right) \bot \left( {ABC} \right)\) và \(\left( {SAB} \right) \bot \left( {SBC} \right)\). Do đó đáp án C và D đúng. Ta có: \(SA \bot \left( {ABC} \right)\,\,\left( {gt} \right)\), mà \(SA \subset \left( {SAC} \right) \Rightarrow \left( {SAC} \right) \bot \left( {ABC} \right)\). Do đó đáp án A đúng. Chọn B. Câu hỏi 31 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D,\,\,AB = 2a\), \(AD = DC = a,\,\,SA = a\) và \(SA \bot \left( {ABCD} \right)\). Tang của góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABCD} \right)\) bằng:
Đáp án: A Phương pháp giải: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc 2 mặt phẳng và vuông góc với giao tuyến. Lời giải chi tiết:
Gọi \(E\) là trung điểm của \(AB\). Dễ dàng chứng minh được \(ADCE\) là hình vuông. \( \Rightarrow CE = AD = a = \dfrac{1}{2}AB \Rightarrow \Delta ACB\) vuông tại \(C \Rightarrow AC \bot BC\). Ta có: \(\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot SC\). \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SC \bot BC\\\left( {ABCD} \right) \supset AC \bot BC\end{array} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA\). \(ADCE\) là hình vuông cạnh \(a \Rightarrow AC = a\sqrt 2 \). Xét tam giác vuông \(SAC:\,\,\tan \angle SCA = \dfrac{{SA}}{{AC}} = \dfrac{1}{{\sqrt 2 }}\). Chọn A. Câu hỏi 32 : Cho hình lăng trụ tứ giác đều \(ABCD.A'B'C'D'\). Mặt phẳng \(\left( {AB'C} \right)\) vuông góc với mặt phẳng nào sau đây?
Đáp án: B Phương pháp giải: Hình lăng trụ tứ giác đều là lăng trụ đứng có đáy là tứ giác đều (hình vuông). Lời giải chi tiết:
Ta có \(ABCD\) là hình vuông \( \Rightarrow AC \bot BD\). Lại có \(BB' \bot \left( {ABCD} \right) \Rightarrow BB' \bot AC\). \( \Rightarrow AC \bot \left( {B'BD} \right)\). Mà \(AC \subset \left( {AB'C} \right) \Rightarrow \left( {AB'C} \right) \bot \left( {B'BD} \right)\). Chọn B. Câu hỏi 33 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\,\,SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\) . Góc giữa 2 mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) bằng :
Đáp án: D Phương pháp giải: Góc giữa 2 mặt phẳng là góc giữa 2 đường thẳng lần lượt thuộc 2 mặt phẳng và vuông góc với giao tuyến. Lời giải chi tiết:
Ta có\(BC//AD \Rightarrow \left( {SAD} \right) \cap \left( {SBC} \right) = Sx\) là đường thẳng đi qua \(S\) và song song với \(AD,BC\). Ta có \(SA \bot AD \Rightarrow SA \bot Sx\). \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB \Rightarrow SB \bot Sx\). \( \Rightarrow \angle \left( {\left( {SAD} \right);\left( {SBC} \right)} \right) = \angle \left( {SA;SB} \right) = \angle ASB\). Xét tam giác vuông \(SAB:\,\,\tan \angle ASB = \dfrac{{AB}}{{SA}} = 1 \Rightarrow \angle ASB = {45^0}\). Vậy \(\angle \left( {\left( {SAD} \right);\left( {SBC} \right)} \right) = {45^0}\). Chọn D. Câu hỏi 34 : Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có mặt \(ABCD\) là hình vuông, \(AA' = \frac{{AB\sqrt 6 }}{2}.\) Xác định góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {C'BD} \right)\).
Đáp án: C Phương pháp giải: + Sử dụng cách xác định góc giữa hai mặt phẳng \(\left( P \right);\left( Q \right)\) \(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\a \bot d;a \subset \left( P \right)\\b \bot \left( Q \right);b \subset \left( Q \right)\end{array} \right. \Rightarrow \) góc tạo bởi \(\left( P \right)\) và \(\left( Q \right)\) là góc tạo bởi hai đường thẳng \(a\) và \(b.\) + Tính toán dựa vào định lý Pytago. Lời giải chi tiết: Gọi \(I\) là giao điểm hai đường chéo của hình vuông \(ABCD\). Khi đó \(I\) là trung điểm của \(BD.\) Xét tam giác \(A'BD\) cân tại \(A' \Rightarrow A'I \bot BD\) và tam giác \(C'BD\) cân tại \(C' \Rightarrow C'I \bot BD\) Ta có \(\left\{ \begin{array}{l}\left( {A'BD} \right) \cap \left( {C'BD} \right) = BD\\A'I \bot BD\\C'I \bot BD\end{array} \right. \Rightarrow \) góc tạo bởi \(\left( {A'BD} \right)\) và \(\left( {C'BD} \right)\) là góc \(A'IC'.\) Gọi \(AB = x \Rightarrow AA' = \frac{{AB\sqrt 6 }}{2} = \frac{{x\sqrt 6 }}{2}\) Xét hình vuông \(ABCD\) có \(AC = BD = x\sqrt 2 \Rightarrow A'C' = x\sqrt 2 ;DI = \frac{{x\sqrt 2 }}{2}\) Xét tam giác \(AA'D\) vuông tại \(A\) có \(A'D = \sqrt {A{{A'}^2} + A{D^2}} = \sqrt {{{\left( {\frac{{x\sqrt 6 }}{2}} \right)}^2} + {x^2}} = \frac{{x\sqrt {10} }}{2}\) Xét tam giác \(A'DI\) vuông tại \(I\) có \(A'I = \sqrt {A'{D^2} - D{I^2}} = \sqrt {{{\left( {\frac{{x\sqrt {10} }}{2}} \right)}^2} - {{\left( {\frac{{x\sqrt 2 }}{2}} \right)}^2}} = x\sqrt 2 \) Vì \(\Delta A'DB = \Delta C'DB\left( {c - c - c} \right) \Rightarrow C'I = A'I = x\sqrt 2 \) Xét tam giác \(A'IC'\) có \(A'I = C'I = A'C' = x\sqrt 2 \) nên \(\Delta A'IC'\) là tam giác đều. Suy ra \(\angle A'IC' = {60^0}.\) Vậy góc tạo bởi \(\left( {A'BD} \right)\) và \(\left( {C'BD} \right)\) là góc \(A'IC'\) bằng \({60^0}.\) Chọn C. Câu hỏi 35 : Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(2a\) và cạnh bên bằng \(a\sqrt 5 \). Gọi \(\left( P \right)\) là mặt phẳng đi qua \(A\) và vuông góc với \(SC\). Gọi \(\beta \) là góc tạo bởi mp\(\left( P \right)\) và \(\left( {ABCD} \right)\). Tính \(\tan \beta \).
Đáp án: A Phương pháp giải: Sử dụng lý thuyết: Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng ấy. Lời giải chi tiết: Gọi \(O\) là tâm hình vuông \(ABCD\). Ta có: \(\left\{ \begin{array}{l}SO \bot \left( {ABCD} \right)\\SC \bot \left( P \right)\end{array} \right.\) \( \Rightarrow \) góc giữa \(\left( {ABCD} \right)\) và \(\left( P \right)\) là góc giữa \(SC\) và \(SO\) hay \(\widehat {CSO}\). Hình vuông \(ABCD\) cạnh \(2a\) nên \(OC = \dfrac{1}{2}AC = \dfrac{1}{2}.2a\sqrt 2 = a\sqrt 2 \). Tam giác \(SOC\) vuông tại \(O\) nên \(SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {5{a^2} - 2{a^2}} = a\sqrt 3 \). \( \Rightarrow \tan \beta = \tan \widehat {CSO} = \dfrac{{OC}}{{SO}} = \dfrac{{a\sqrt 2 }}{{a\sqrt 3 }} = \dfrac{{\sqrt 6 }}{3}\). Chọn A. Câu hỏi 36 : Cho hình chóp \(S.ABC\). \(SA \bot \left( {ABC} \right),\,\,SA = \dfrac{{3a}}{2}\). \(\Delta ABC\) là tam giác đều cạnh \(a\). Khi đó, góc tạo bởi hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) là:
Đáp án: B Phương pháp giải: Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng lần lượt thuộc 2 mặt phẳng và vuông góc với giao tuyến. Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(BC\) ta có \(AM \bot BC\) và \(AM = \dfrac{{a\sqrt 3 }}{2}\). \(\left\{ \begin{array}{l}BC \bot AM\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM\). Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SM \bot BC\\\left( {ABC} \right) \supset AM \bot BC\end{array} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SM;AM} \right) = \angle SMA\). Trong tam giác vuông \(SAM\) có: \(\tan \angle SMA = \dfrac{{SA}}{{AM}} = \dfrac{{\dfrac{{3a}}{2}}}{{\dfrac{{a\sqrt 3 }}{2}}} = \sqrt 3 \Rightarrow \angle SMA = {60^0}\). Vậy \(\angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = {60^0}\). Chọn B. Câu hỏi 37 : Cho hình lập phương \(ABCD.A'B'C'D'\). Tính cosin của góc giữa hai mặt phẳng \(\left( {BDA'} \right)\) và \(\left( {ABCD} \right)\).
Đáp án: D Phương pháp giải: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến. Lời giải chi tiết: Gọi \(O = AC \cap BD\). Ta có: \(\left\{ \begin{array}{l}BD \bot AO\\BD \bot AA'\end{array} \right. \Rightarrow BD \bot \left( {AOA'} \right) \Rightarrow BD \bot OA'\). \(\left\{ \begin{array}{l}\left( {BDA'} \right) \cap \left( {ABCD} \right) = BD\\\left( {BDA'} \right) \supset OA' \bot BD\\\left( {ABCD} \right) \supset OA \bot BD\end{array} \right. \Rightarrow \angle \left( {\left( {BDA'} \right);\left( {ABCD} \right)} \right) = \angle \left( {OA';OA} \right) = \angle A'OA\) Giả sử \(ABCD.A'B'C'D'\) là hình lập phương cạnh bằng 1 \( \Rightarrow AC = \sqrt 2 \Rightarrow OA = \dfrac{{\sqrt 2 }}{2}\). Trong tam giác vuông \(OAA'\) có: \(OA' = \sqrt {O{A^2} + AA{'^2}} = \sqrt {\dfrac{1}{2} + 1} = \dfrac{{\sqrt 6 }}{2}\). \( \Rightarrow \cos \angle A'OA = \dfrac{{OA}}{{AA'}} = \dfrac{{\dfrac{{\sqrt 2 }}{2}}}{{\dfrac{{\sqrt 6 }}{2}}} = \dfrac{{\sqrt 3 }}{3}\). Vậy \(\cos \angle \left( {\left( {BDA'} \right);\left( {ABCD} \right)} \right) = \dfrac{{\sqrt 3 }}{3}\). Chọn D. Câu hỏi 38 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,\,\,AB = 2,\,\,BC = 2\sqrt 3 \), cạnh bên \(SA = \dfrac{{\sqrt 3 }}{2}\) vuông góc với mặt phẳng \(\left( {ABC} \right)\). Gọi \(M\) là trung điểm của \(AB\), tính tan của góc giữa \(\left( {SMC} \right)\) và \(\left( {ABC} \right)\).
Đáp án: A Phương pháp giải: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến. Lời giải chi tiết: Trong \(\left( {ABC} \right)\) kẻ \(AH \bot MC\,\,\left( {H \in MC} \right)\) ta có: \(\left\{ \begin{array}{l}MC \bot AH\\MC \bot SA\end{array} \right. \Rightarrow MC \bot \left( {SAH} \right) \Rightarrow MC \bot SH\). \(\left\{ \begin{array}{l}\left( {SMC} \right) \cap \left( {ABC} \right) = MC\\\left( {SMC} \right) \supset SH \bot MC\\\left( {ABC} \right) \supset AH \bot MC\end{array} \right. \Rightarrow \angle \left( {\left( {SMC} \right);\left( {ABC} \right)} \right) = \angle \left( {SH;AH} \right) = \angle SHA\). Dễ thấy \(\Delta AMH \sim \Delta CMB\,\,\left( {g.g} \right) \Rightarrow \dfrac{{AH}}{{BC}} = \dfrac{{AM}}{{MC}}\). \( \Rightarrow AH = \dfrac{{BC.AM}}{{MC}} = \dfrac{{2\sqrt 3 .1}}{{\sqrt {{{\left( {2\sqrt 3 } \right)}^2} + {1^2}} }} = \dfrac{{2\sqrt {39} }}{{13}}\). Trong tam giác vuông \(SAH:\,\,\tan \angle SHA = \dfrac{{SA}}{{AH}} = \dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{{2\sqrt {39} }}{{13}}}} = \dfrac{{\sqrt {13} }}{4}\). Chọn A. Câu hỏi 39 : Hình chóp đều \(S.ABCD\) có \(SA = AB = a\). Cosin góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) bằng
Đáp án: D Phương pháp giải: Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến. Lời giải chi tiết: Gọi \(M\) là trung điểm của \(SA\). Do \(S.ABCD\) đều nên \(SA = SB = SC = SD\). Mà \(SA = AB = a\) nên các tam giác \(SAB,SAD\) là tam giác đều. Khi đó \(BM \bot SA,DM \bot SA\). Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SAD} \right) = SA\\BM \subset \left( {SAB} \right),DM \subset \left( {SAD} \right)\\BM \bot SA,DM \bot SA\end{array} \right.\) \( \Rightarrow \) góc giữa \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) bằng \(\widehat {\left( {BM,DM} \right)} = \widehat {BMD}\). Dễ thấy \(BM = DM = \dfrac{{a\sqrt 3 }}{2},BD = a\sqrt 2 \). \( \Rightarrow \cos \widehat {BMD} = \dfrac{{B{M^2} + D{M^2} - B{D^2}}}{{2BM.DM}}\) \( = \dfrac{{\dfrac{{3{a^2}}}{4} + \dfrac{{3{a^2}}}{4} - 2{a^2}}}{{2.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 }}{2}}} = - \dfrac{1}{3}\). Chọn D. Câu hỏi 40 : Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và \(SA = SC = a\),\(SB = 2a\). Gọi O là tâm của mặt cầu ngoại tiếp hình chóp S.ABGóc giữa hai mặt phẳng (SBO) và (SBC) bằng
Đáp án: D Phương pháp giải: +) Xác định tâm \(O\) của mặt cầu ngoại tiếp khối chóp \(SABC.\) +) Góc giữa hai mặt phẳng là góc giữa hai đường thẳng thuộc hai mặt phẳng cùng vuông góc với giao tuyến. Lời giải chi tiết:
Ta có: \(\Delta SBC\) vuông tại \(S \Rightarrow M\) là tâm đường tròn ngoại tiếp \(\Delta SBC\) với \(M\) là trung điểm của \(BC.\) Gọi \(I,\,\,H\) lần lượt là trung điểm của các cạnh \(SA,\,\,SC.\) Qua \(M,\) dựng đường thẳng \(d//SA\) Qua \(I,\,\,\) dựng đường thẳng song song với \(SM,\) cắt \(d\) tại \(O.\) \( \Rightarrow O\) là tâm mặt cầu ngoại tiếp khối chóp \(SABC.\) Ta có: \(\left( {SBO} \right) \cap \left( {SBC} \right) = SB.\) Ta có: \(\left\{ \begin{array}{l}SB \bot OM\\SB \bot HM\end{array} \right. \Rightarrow SB \bot \left( {OMH} \right) \Rightarrow SB \bot OH.\) Có: \(\left\{ \begin{array}{l}MH \bot SB\,\,\left( {MH//SC} \right)\\OH \bot SB\,\,\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow \angle \left( {\left( {SBO} \right),\,\left( {SBC} \right)} \right) = \angle \left( {MH,\,OH} \right) = \angle OHM\) Xét \(\Delta OHM\) vuông tại \(M\) ta có: \(\tan OHM = \dfrac{{OM}}{{HM}} = \dfrac{{\dfrac{1}{2}SA}}{{\dfrac{1}{2}SC}} = \dfrac{{SA}}{{SC}} = \dfrac{a}{a} = 1 \Rightarrow \angle OHM = {45^0}.\) Chọn D.
|